文章目录
什么是强化学习
“强化学习”这个词,指一类问题,也指解决这类问题的方法。
强化学习的两个基本特征
- 试错。学习者不会被告知应该采取什么动作,而是自己通过尝试去发现哪些动作收益最大。
- 延迟收益。动作既有即时收益,也有长期收益。
强化学习的其它特征
仿生。实际上“强化”最早源于巴甫洛夫。
强化学习不同于有监督学习
后者学习的是标注。
前者从智能体自身的经验中学习。
强化学习不同于无监督学习
后者的目的是,寻找数据中的隐含结构。
前者的目的是,最大化收益信号。
强化学习不同于进化方法
后者只看结果,不问过程。经典实例就是,门齿楞,这个突变毫无作用,但因为搭上了有用突变的顺风车,而在进化中得以保留。获取结果后,认为过程中所有的动作都有功劳。
前者则充分利用过程,评估每一个动作的价值。
进化方法是对整个策略的评估,强化学习则是对每个动作的评估。
强化学习的独特挑战
explore和exploit的权衡。
但本书并不特别关心平衡两者的具体方法,而是关心要不要去平衡它们。
强化学习典例
对弈。
羚羊幼崽30分钟学会站立和奔跑。
做早餐。
机器人决定工作还是充电。
总结:与不确定的环境进行交互,有目标,需要远见和规划。
强化学习的要素
- 策略
- 即时收益
- 长期价值
- 环境模型
确定价值比确定收益难得多,是强化学习算法中最重要的部分。
目标就是最大化长期总收益,也就是价值。
如果没有环境模型,就只是单纯的试错。有环境模型时,可以对环境做出预测,从而有所规划。
策略是状态到每个动作选择概率的映射。
强化学习的适用范围
可以没有对手,与环境博弈。
可以在时间上连续(对弈是离散的)。
可以用于无穷大的状态集。
可以利用游戏规则以外的先验信息。
强化学习学术主线
- 最优控制
- 试错学习
- 时序差分
解决强化学习问题的一般框架
有限马尔可夫决策过程是解决强化学习问题的一般框架。

赌博机
两个影响因素
- 赌博机是否平稳,即每个臂的分布是否会变
- 每个臂的分布的方差大小,如果大则需要更多explore
平稳赌博机和非平稳赌博机
前者的朴素实现:

思想就是,利用已知的信息,求出一个臂收益的平均值,作为其未来的收入预期。
上面的例子是最容易理解的。实际上可以借助上一次的结果较快算出新的平均值。因为:
新平均值 x n = 旧平均值 x (n-1) + 最新收益

2.3式的理解,随着n的增大,单次收益对整体平均值的影响越来越小。
对于不平稳的赌博机,我们更关心较新的值。把2.3中的步长n换成常数,即可让较新的值对结果产生较大影响。权重是一个等比数列,权重和为1。这个方法称为指数近因加权平均。


这里需要温习一下无穷级数的收敛性判断。可以用积分判别法。lnx+1不收敛,1/x+1则收敛。所以采样平均能在采样次数足够多的前提下收敛到真值。至于常数步长,由于不是递减,显然是发散的。
乐观初始值的理解
试想,如果每个臂的估计初始值为5(超过所有臂的最高收益),那系统就总会认为没选过的臂是更好的。任何实际选择都会带来失望,永远对没选过的抱有幻想。
一开始我以为原始贪心算法一遇到正的就会固定,看了知乎专栏发现其实原始贪心算法也会做一轮探索。所以初始值为0和为5的区别在哪里?
第一轮每个臂的收益都下降了,但下降程度不同。赌徒随后开始大规模操作第一轮的最优(跟原始贪心算法一样),但随后他发现这个不再是最优了(因为对于每条臂,都是越摇越差)。因此,乐观初始值比较大的时候,每个臂都会被选择多次,而不是一次。这样可以缓解原始贪心中的第一轮的误导。
对于非平稳问题,初始值的作用就不大了。
赌博机问题的求解方法
全能全知(Omniscient)
即已经知道回报概率,那最直接的策略就是一直玩这一台。后面的每个策略的探索表现都会和上帝的答案来比较。
随机算法(Random)
每一轮随机地去拉一个摇臂。
贪心算法(Greedy)
先把所有的摇臂都拉一次,然后选择回报最好的老虎机一直玩下去。这种策略很明显不鼓励进行探索,而且很容易被每个摇臂第一遍的回报结果误导。
ucb
upper confidence bound
epsilon-greedy实际上是一种盲目的选择,因为它不太会选择接近贪心或者不确定性特别大的动作。在命中epsilon时,在包括贪心动作在内的所有动作中等概率选择(epsilon/n)。
而ucb体现的是不确定性优先,选择较少的臂的修正项会比较大。
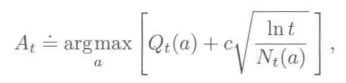
ln t随着轮数的增加而增大,Nt(a)则是截至第t轮选择a的次数。
梯度赌博机算法
在dl,有一句话:“二分类单输出用sigmoid,多分类或多输出用softmax。”
我并不熟悉dl和分类问题。我的理解是这样的:
一个物体属于a类、b类、c类的可能性如果用整数表示为2,3,5,
那么hardmax的结果是5,认为这个物体属于c类。
而softmax则不同,softmax的结果是0.04201007, 0.11419519, 0.8437947(公式见下图)。三个值分别表示这个物体属于a、b、c类的概率。
经过使用指数形式的Softmax函数能够将差距大的数值距离拉的更大。
至于为什么要用sigmoid和softmax,我想是为了在不改变性质的前提下,用可导函数代替不可导函数,方便数学计算。而且相比hardmax,softmax保留了更多信息,肯定更加精确周到。
梯度赌博机算法引入了偏好函数,所有臂的偏好函数初始时是一样的(如0)。
偏好函数的更新:
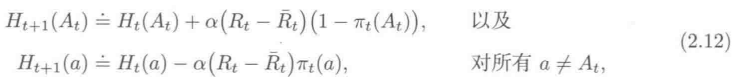
肤浅的解释是,如果t时刻选一个臂,表现比t时刻的均值要好,那就提高偏好,反之降低。
每次对臂的选择取决于下式:
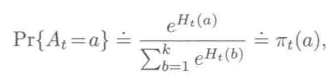
肤浅的解释是,臂的偏好函数越大,选择这个臂的可能性就越大。
从2.12式可以看出,基准项Rt拔的引入可以减小减小更新项的方差,相比无基准项时收敛更快。
从结果来看,α大的时候收敛更快。
2.12式是怎么来的,以及为什么叫梯度赌博机算法?由2.13推导可以得到2.12。

将每一时刻所有选择的期望看作此时刻所有偏好函数的因变量。
这也是比较自然的,因为偏好影响选择,选择影响性能。
2.13中q*(x)我们无法获得,但可以用期望来代替。实际可用的就是2.12。
汤普森采样
https://www.cnblogs.com/gczr/p/11220187.html
棒球运动员的例子很生动。
我们一开始有一些先验知识(大概了解棒球运动员的击球率区间);
然后根据本赛季棒球运动员的实际表现来调整击球率的概率分布。
相比朴素除法,我们最后获得的不是一个概率,而是概率的概率分布,即:本赛季的击球率的概率分布。
其优势在于,不太受数据量的影响,不管是赛季刚开始,或是上场比较少,都能不丢失信息地刻画出击球率(如果上场比较少,那么击球率的分布就会比较分散。因为数据少所以不确定性大,从图上是能看出来的),而不是一个扁平的值。
赌博机问题与真正强化学习之间的距离
赌博机问题是上下文无关的,是非关联的,即动作不会影响情境。动作只影响当次收益。
真正的强化学习中,动作不只影响当次收益,还会影响情境。往往有多种情境。
我的理解是,你对赌博机的操作,会影响你玩的下一台赌博机的编号。这就是动作影响情境,不止一种情境。
按我理解,这是一种比较极端的非平稳过程(臂的收益分布不是渐变的,而是跳变的,因为根本就不是同一台赌博机了,所以上文的非平稳方法很大可能没效果)。
强化学习要做的,就是利用赌博机的编号信息,形成与任务相关的策略。