LeetCode 1168. Optimize Water Distribution in a Village

原题链接在这里：https://leetcode.com/problems/optimize-water-distribution-in-a-village/description/

题目：

There are n houses in a village. We want to supply water for all the houses by building wells and laying pipes.

For each house i, we can either build a well inside it directly with cost wells[i - 1] (note the -1 due to 0-indexing), or pipe in water from another well to it. The costs to lay pipes between houses are given by the array pipes where each pipes[j] = [house1j, house2j, costj] represents the cost to connect house1j and house2j together using a pipe. Connections are bidirectional, and there could be multiple valid connections between the same two houses with different costs.

Return the minimum total cost to supply water to all houses.

Example 1:

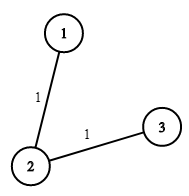
Input: n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
Output: 3
Explanation: The image shows the costs of connecting houses using pipes.
The best strategy is to build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the total cost is 3.

Example 2:

Input: n = 2, wells = [1,1], pipes = [[1,2,1],[1,2,2]]
Output: 2
Explanation: We can supply water with cost two using one of the three options:
Option 1:
  - Build a well inside house 1 with cost 1.
  - Build a well inside house 2 with cost 1.
The total cost will be 2.
Option 2:
  - Build a well inside house 1 with cost 1.
  - Connect house 2 with house 1 with cost 1.
The total cost will be 2.
Option 3:
  - Build a well inside house 2 with cost 1.
  - Connect house 1 with house 2 with cost 1.
The total cost will be 2.
Note that we can connect houses 1 and 2 with cost 1 or with cost 2 but we will always choose the cheapest option. 

Constraints:

• 2 <= n <= 104
• wells.length == n
• 0 <= wells[i] <= 105
• 1 <= pipes.length <= 104
• pipes[j].length == 3
• 1 <= house1j, house2j <= n
• 0 <= costj <= 105
• house1j != house2j

题解：

Let us assume there is no wells. Transform all the wells cost to the edges.
There is a hidden house, house 0. All the wells cost are the edges cost from house 0.

Then along with piples cost, we can sort all the edges cost.

Then we want to connect the components. For a new edge, if two nodes are not connected, use this edge cost to connect since it is the cheapest.

Time Complexity: O(mlogm). m = piples.length + n.

Space: O(m).

AC Java:

 1 class Solution {
 2     int[] parent;
 3     public int minCostToSupplyWater(int n, int[] wells, int[][] pipes) {
 4         parent = new int[n + 1];
 5         List<int[]> edges = new ArrayList<>();
 6         for(int i = 0; i < n; i++){
 7             parent[i + 1] = i + 1;
 8             edges.add(new int[]{0, i + 1, wells[i]});
 9         }
10         
11         for(int[] pipe : pipes){
12             edges.add(pipe);
13         }
14         
15         Collections.sort(edges, (a, b) -> Integer.compare(a[2], b[2]));
16         
17         int res = 0;
18         for(int [] e : edges){
19             int x = root(e[0]);
20             int y = root(e[1]);
21             if(x != y){
22                 res += e[2];
23                 parent[x] = y;
24             }
25         }
26         
27         return res;
28     }
29     
30     private int root(int i){
31         if(i != parent[i]){
32             parent[i] = root(parent[i]);
33         }
34         
35         return parent[i];
36     }
37 }