TwoConvexShapes
Statement
给定 \(n\times m\) 的网格,包含 ?,B,W 三种字符,其中 ? 表示可以填 B 或 W。问在所有的填法中有多少种填法满足如下条件:
B和W颜色均为连通的,即不存在一个颜色,四个方向中没有这个颜色(除了该颜色只有 \(1\) 个的情况)。- 不存在一列或一行,同种颜色的两个位置之间存在其他颜色。
Solution
Hint 1: 考虑怎样的填法满足条件?
针对其中 \(1\) 个颜色讨论即可,剩余的位置即为另一个颜色。假设对于 B 讨论,则对于列的限制,不能有一列上存在两个 B 的连通块,也就是说在集中在上方,或集中在下方。对于行的限制,其实就是要么单调不降,要么单调不升。
注意:下图只是给出了 \(2\) 种情况,这样排列是不合法的,但是只保留蓝色部分或红色部分即是合法的。
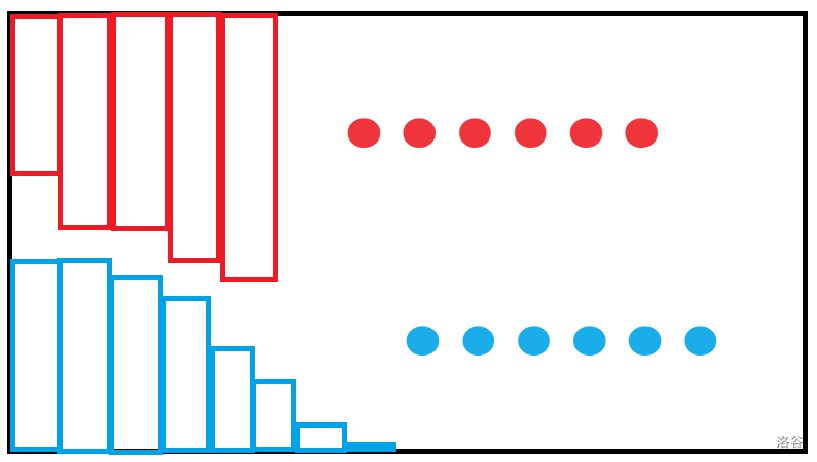
Hint 2: 如何快速的统计方案数?
发现规律后,可以对于红色部分的答案和蓝色部分的答案分别计算。以红色为例,设 \(f_{j,i,0/1}\) 表示第 \(j\) 列,已经到达第 \(i\) 行,是上升趋势 / 下降趋势。转移进需要判断当前第 \(j\) 列能否填至第 \(i\) 行即可,这个可以提前预处理。
//预处理代码,pb[i][j] 表示第 j 列前 i 行能否全填 B,sb[i][j] 表示第 j 列前 i 行能否全填 B;对于 W 同理
for (int j = 1; j <= m; j ++) {
pb[0][j] = pw[0][j] = 1;
for (int i = 1; i <= n; i ++) {
pb[i][j] = pb[i - 1][j] & (grid[i - 1][j - 1] != 'W');
pw[i][j] = pw[i - 1][j] & (grid[i - 1][j - 1] != 'B');
}
}
for (int j = 1; j <= m; j ++) {
sb[n + 1][j] = sw[n + 1][j] = 1;
for (int i = n; i >= 1; i --) {
sb[i][j] = sb[i + 1][j] & (grid[i - 1][j - 1] != 'W');
sw[i][j] = sw[i + 1][j] & (grid[i - 1][j - 1] != 'B');
}
}
预处理出后,便可以转移:\(f_{j,i,0}=\sum_{k=0}^{i}f_{j-1,k,0}\)。对于 \(1\) 也是同理的,只需要更改 \(k\) 的上下界即可。对于蓝色部分,其实没必要再更改到下面,会不好写,所以其实等价于计算 W 颜色的红色部分,因此只需稍作更改转移的条件即可。
Hint 3: 检验是否算重?
都这么问了,那肯定是算重了!仅针对于 \(1\) 个部分而言,光单调不降和单调不升就会算重,即全部是一个高度(不升也不降)会算 \(2\) 次,所以减掉 \(1\) 次即可(不过,前提是能保证同一个高度是合法的)。
但是,对于蓝色和红色部分会算重吗?答案是肯定的。当都填满了若干列,剩余列均为填满的时候,会算重(如图)。
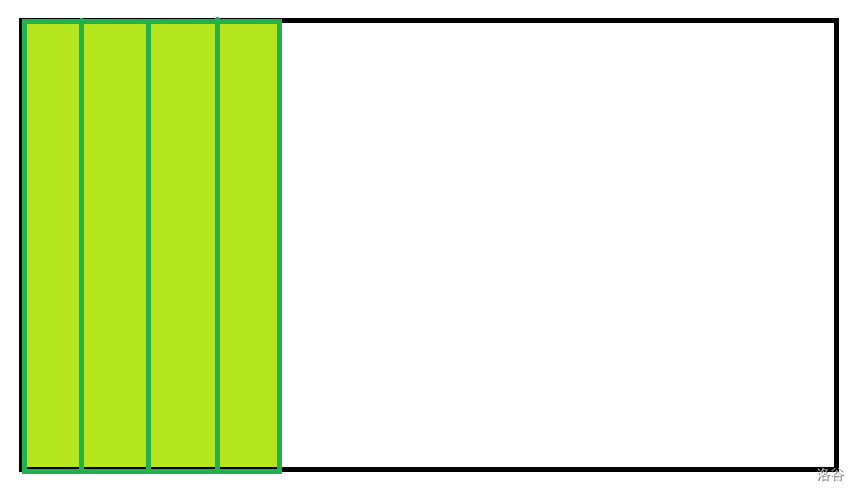
Ok,那么这样你就得到了一个 \(O(n^2m)\) 的做法,已经能通过此题。不过,作为完美主义者,我们要进一步优化,其实优化也很简单——只需要做一个前缀和即可,因为你发现上面的转移即为一个前缀和。这样,可以做到 \(O(nm)\) 了,所以 \(n\) 完全可以开到 \(10^4\) 的。
Code
注意:省略了取模板子和头文件,所以复制是 AC 不了的。
const int N = 55;
Mint f[N][N][2];
int pb[N][N], pw[N][N], sb[N][N], sw[N][N];
class TwoConvexShapes {
public:
int countWays(std::vector<string> grid) {
int n = grid.size(), m = grid[0].size();
for (int j = 1; j <= m; j ++) {
pb[0][j] = pw[0][j] = 1;
for (int i = 1; i <= n; i ++) {
pb[i][j] = pb[i - 1][j] & (grid[i - 1][j - 1] != 'W');
pw[i][j] = pw[i - 1][j] & (grid[i - 1][j - 1] != 'B');
}
}
for (int j = 1; j <= m; j ++) {
sb[n + 1][j] = sw[n + 1][j] = 1;
for (int i = n; i >= 1; i --) {
sb[i][j] = sb[i + 1][j] & (grid[i - 1][j - 1] != 'W');
sw[i][j] = sw[i + 1][j] & (grid[i - 1][j - 1] != 'B');
}
}
std::vector<Mint> ics(n + 1, 1), dcs(n + 1, 0);
f[0][0][0] = f[0][n][1] = 1, dcs[n] += 1;
for (int j = 1; j <= m; j ++) {
for (int i1 = 0; i1 <= n; i1 ++) {
if (!pb[i1][j] || !sw[i1 + 1][j]) continue;
f[j][i1][0] = ics[i1];
f[j][i1][1] = dcs[n] - (!i1 ? 0 : dcs[i1 - 1]);
}
ics[0] = f[j][0][0], dcs[0] = f[j][0][1];
for (int i1 = 1; i1 <= n; i1 ++)
ics[i1] = ics[i1 - 1] + f[j][i1][0], dcs[i1] = dcs[i1 - 1] + f[j][i1][1];
}
Mint res = 0;
for (int i = 0; i <= n; i ++)
res += f[m][i][0] + f[m][i][1] - (min(f[m][i][0].v, f[m][i][1].v) > 0);
memset(f, 0, sizeof f);
for (int i = 0; i <= n; i ++) ics[i] = 1, dcs[i] = 0;
f[0][0][0] = f[0][n][1] = 1, dcs[n] += 1;
for (int j = 1; j <= m; j ++) {
for (int i1 = 0; i1 <= n; i1 ++) {
if (!pw[i1][j] || !sb[i1 + 1][j]) continue;
f[j][i1][0] = ics[i1];
f[j][i1][1] = dcs[n] - (!i1 ? 0 : dcs[i1 - 1]);
}
ics[0] = f[j][0][0], dcs[0] = f[j][0][1];
for (int i1 = 1; i1 <= n; i1 ++)
ics[i1] = ics[i1 - 1] + f[j][i1][0], dcs[i1] = dcs[i1 - 1] + f[j][i1][1];
}
for (int i = 0; i <= n; i ++)
res += f[m][i][0] + f[m][i][1] - (min(f[m][i][0].v, f[m][i][1].v) > 0);
memset(f, 0, sizeof f);
f[0][0][0] = f[0][n][1] = 1;
for (int j = 1; j <= m; j ++) {
if (pw[0][j] && sb[1][j]) {
f[j][0][0] += f[j - 1][0][0];
f[j][0][1] += f[j - 1][0][1] + f[j - 1][n][1];
}
if (pw[n][j] && sb[n + 1][j]) {
f[j][n][0] += f[j - 1][0][0] + f[j - 1][n][0];
f[j][n][1] += f[j - 1][n][1];
}
}
res -= (f[m][0][0] + f[m][0][1] - (min(f[m][0][0].v, f[m][0][1].v) > 0) + f[m][n][0] + f[m][n][1] - (min(f[m][n][0].v, f[m][n][1].v) > 0));
return res.v;
}
};