SRM 550 - 500 CheckerExpansion
Description
起初 \((0,0)\) 点 Alice 填为了红色,接下来 \(t\) 次操作 Alice 和 Bob 轮流操作,如果 \((x-1,y-1)\) 位置被另一方填了且 \((x-2,y)\) 为空;或 \((x-1,y-1)\) 为空且 \((x-2,y)\) 被另一方填了,则当前方将填 \((x,y)\)。
给定 \(x,y,h,w\) 表示一个方格,输出该方格内的所有点(A 表示 Alice 填的,B 表示 Bob 填的)。
\(1\le x,y,t\le 10^{12},1\le h,w\le 50\)
Solution
拿到这个题感觉没有什么思路,于是不妨先打个表(如图)
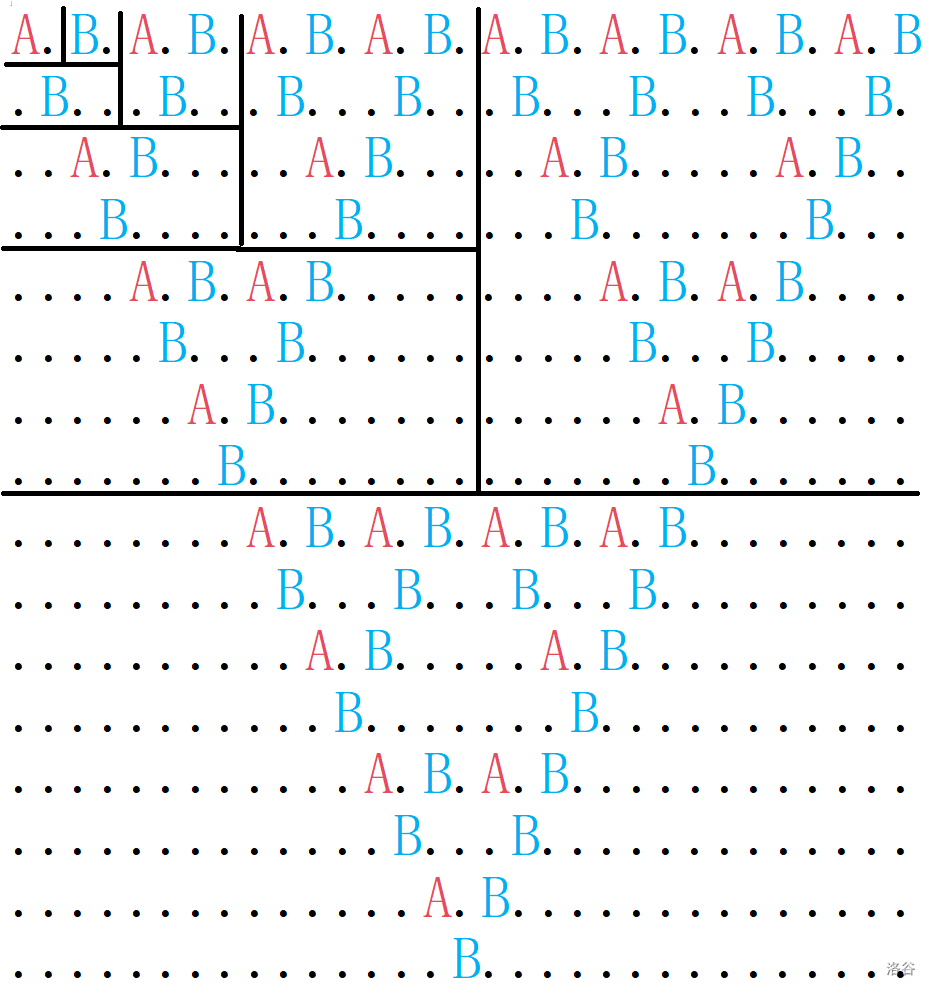
注意,这里左上角为 \((0,0)\)。不错呦,有规律诶,是图形的分形!于是乎,考虑分治,不难发现每次划分为 \(3\) 部分,不断地将坐标缩小至左上角部分并不断分治。不难发现,这样就可以判断出任意一个点是否被填了。若要判断 A 还是 B,只需要判断 \(\frac{x+y}{2}\) 的奇偶性即可。
具体分治过程,详见代码。
Code
class CheckerExpansion {
public:
int lg2(LL x) {
int res = 0;
while (x != 1) res ++, x /= 2;
return res;
}
int Exist(LL x, LL y) {
if ((x + y & 1) || (x < y)) return 0;
LL turn = x + y >> 1;
if (turn <= 1) return 1;
LL h = (1ll << lg2(turn)), w = (1ll << lg2(turn)) * 2;
if (x < w && y < h) return 0;
if (y >= h) y -= h, x -= h;
if (x >= w) x -= w;
return Exist(x, y);
}
std::vector<string> resultAfter(LL turn, LL x, LL y, int h, int w) {
std::vector<string> res;
for (LL i = y + w - 1; i >= y; i --) {
string tmp;
for (LL j = x; j <= x + h - 1; j ++) {
if ((i + j >> 1) >= turn || !Exist(j, i)) tmp += '.';
else if ((i + j >> 1) & 1) tmp += 'B';
else tmp += 'A';
}
res.push_back(tmp);
}
return res;
}
};