1. 深度学习的基本原理
深度学习的起源最早可以追溯到感知机,所谓的感知机即只有一个神经元的单层神经网络,它只能完成一个简单的线性分类任务,而要解决非线性的任务,一是可以引入非线性的激活函数,二是可以通过叠加多层网络进而使网络具有非线性的表达能力。早期的神经网络一般都是通过全连接层来实现的,由于全连接层无法实现参数共享,因而全连接层很自然地就会带来一个缺点:权重数量较多,因此如果加深网络层数带来的一个直接问题就是网络难以训练,因而早期的网络层数一般都比较浅,直至后来出现了卷积神经网络,ResNet 等相应的改进之后,神经网络才慢慢朝着网络层数越来越深的方向进行发展。
在 20 世纪 90 年代就曾有人从理论上证明了只有一个隐层的浅层神经网络就足以拟合出任意的函数,因此神经网络这种方法是有很强的表达能力的。但可以拟合出任意的函数与真正能实现具体任务的预测之间还需要一个桥梁来进行连接,这就是模型的训练,模型的训练其实基本包含了两个过程,一个是正向传播的过程,另外一个则是反向传播的过程,正向传播即是数据输入到数据输出的过程,其顺着网络进行计算便可最终得到一系列的预测值,而反向传播则是在得到预测值之后,进行损失函数的计算,并最终计算损失函数对每个权重或偏置的偏导,实现对参数进行更新的过程。可以说训练的核心思想就是通过更新权重参数使推理结果不断趋近于真实值,其实这有点类似于数学上的动态规划。
2. 目标检测的评价指标
2.1 IoU (Intersection over Union)
对于一个预测出来的边界框 (Bonding Box) 来说究竟要有多准确才能认为该预测出来的边界框 (Bonding Box) 是正确的呢,这便需要引入到一个概念——交并比 (Intersec- tion over Union, IoU)。IoU的计算公式如式(1)所示,IoU 衡量的是区域 A 和区域 B 的重叠程度,即两个区域重叠的部分占两者总面积的比例。一般来说当预测出来的边界框 与真实区域 (Ground Truth) 的 IoU 大于 0.5 时,即可认为该预测出来的边界框 (Bonding Box) 是正确的。
\begin{equation}\label{equ:IoU}
IoU_B^A = \frac{A \cap B}{A \cup B}
\end{equation}
2.2 mAP (mean Average Precision)
了解了IoU 之后,接下来便需要了解如何衡量一个目标检测模型的性能,这里所采用的指标就是平均精度均值 (mean Average Precision, mAP),但是在介绍 mAP 之前必须还得引入以下几个概念:TP,FP,FN,Precision,Recall 和 AP。
首先对于只预测一个类别的情况而言,预测的结果可以分为以下三类:
(1) 真正例 (True Positive, TP):预测值与真实值(Ground Truth) 的 IoU 大于 0.5;
(2) 假正例(False Positive, FP):Positive 指的是预测出来的是正样本,也即是模型认为
该区域内包含目标,但实际上预测值与真实值 (Ground Truth) 的 IoU 却小于 0.5;
(3) 假反例 (False Negative, FN):Negative 指的是预测出来的是负样本,也即是模型认为该区域内不包含目标,但实际上该区域内应该要有一个 IoU 大于 0.5 的预测值。
通俗一点来讲,FP 可以理解为框错,而FN 可以理解为漏框,那么对于一个预测出来的边界框(Bonding Box) 与真实值(Ground Truth) 的IoU 只有 0.4 的情况,应该要理解为框错 (FP) 还是漏框 (FN) 呢,正确的答案应该是都算,因为对于 FP 而言是站在预测值的角度来说的,换而言之只要预测值与真实值(Ground Truth) 的IoU 小于 0.5,那么就都应该算作 FP;相反对于 FN 而言是站在真实值 (Ground Truth) 的角度来说的,换而言之只要没有预测值和该真实值 (Ground Truth) 的 IoU 大于 0.5,那么就应该算作 FN。特别需要注意的是,对于同一个真实值 (Ground Truth) 来说只能出现一次 TP 的情况,也就是说即使有多个预测值与该真实值 (Ground Truth) 的 IoU 大于 0.5,那也只能算一个TP,其余的都只能算作 FP。
那么对于多个类别来说又是如何处理的呢,比方如果有一个预测值的 IoU 已经大于 0.5 了,但是所预测的类别(Class) 却是错的,那么应归为哪一类呢,严格来讲这种情况是不会出现的,因为在统计 TP,FP 和 FN 这三个值时默认只统计一个类别,也就是说如果所预测的类别已经错了,那么它所预测的边界框 (Bonding Box) 就不会在这一类别 (Class) 里进行统计,而是在它所预测出的那个类别 (Class) 里进行统计。
有了 TP,FP,FN 这三个概念之后就可以再引入两个更重要的概念了——查准率(Precision) 和召回率 (Recall)(也叫查全率),他们的定义如式(2)所示,同样查准率 (Precision) 是站在预测值的角度来说的,其刻画的是模型所检测出来的目标有多大概率是准确的,而召回率 (Recall) 则是站在真实值的角度来说的,其刻画的是所有的真实目标有多大概率能被模型所检测出来。但是这又有一个问题,就是查准率 (Precision) 和召回率 (Recall) 天生就像是一个皮球的两面,看到的这面多了,另外一面能看到的就会变少,两者往往是不可同时兼得的,那么又是否能有一个指标来衡量目标检测模型 的性能,既能体现查准率 (Precision) 又能体现召回率 (Recall) 呢,那答案就是平均精度(Average Precision, AP)。
\begin{equation}\label{equ:2}
\begin{aligned}
Precision & = \frac{TP}{TP + FP} \\
Recall & = \frac{TP}{TP + FN}
\end{aligned}
\end{equation}
由于目标检测模型在输出预测值的同时一般都还会附带着模型认为该预测值是否准确的衡量指标——置信度 (Confidence),而如果调高置信度 (Confidence) 的阈值,那么查准率 (Precision) 就会提高,但召回率 (Recall) 却会降低;相反,如果调低置信度(Confidence) 的阈值,那么召回率(Recall) 会提高,查准率(Precision) 会降低。于是通过调整置信度(Confidence) 的阈值,我们可以得到所有召回率(Recall) 和查准率(Precision) 的对应关系,然后以召回率 (Recall) 为 x 轴,查准率 (Precision) 为 y 轴,并将它们的对应关系一一在图像中以点的形式标注出来,最后连成一段一段的折线,如图 1 所示, 这便是 PR 曲线。再者,根据 PASCAL Visual Object Classes Challenge 2012 (VOC2012) 中平均精度 (AP) 的计算方法,应该还需要对 PR 曲线进行一定的平滑处理,也即是认为所有的查准率 (Precision) 都应该只算局部召回率 (Recall) 最大时那个点的查准率(Precision),如图 2 所示,最后再用微积分的方法求出该曲线与坐标轴围成面积的大小即为最后的平均精度 (Average Precision, AP)。AP 有了, 那么平均精度均值 (mean Average Precision, mAP) 就很好理解了,也即是把预测的所有类别 (Class) 的 AP 取其平均。
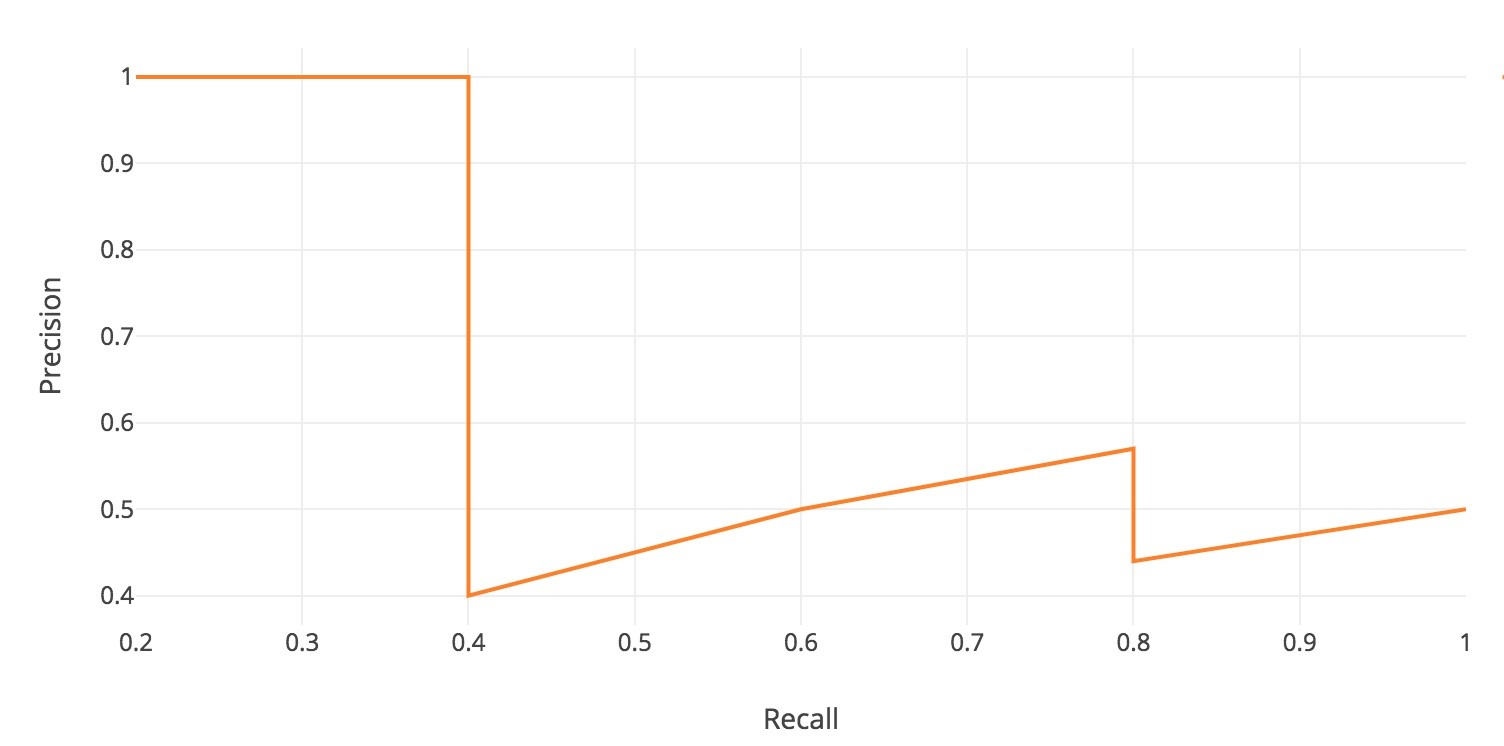
图 1 PR曲线
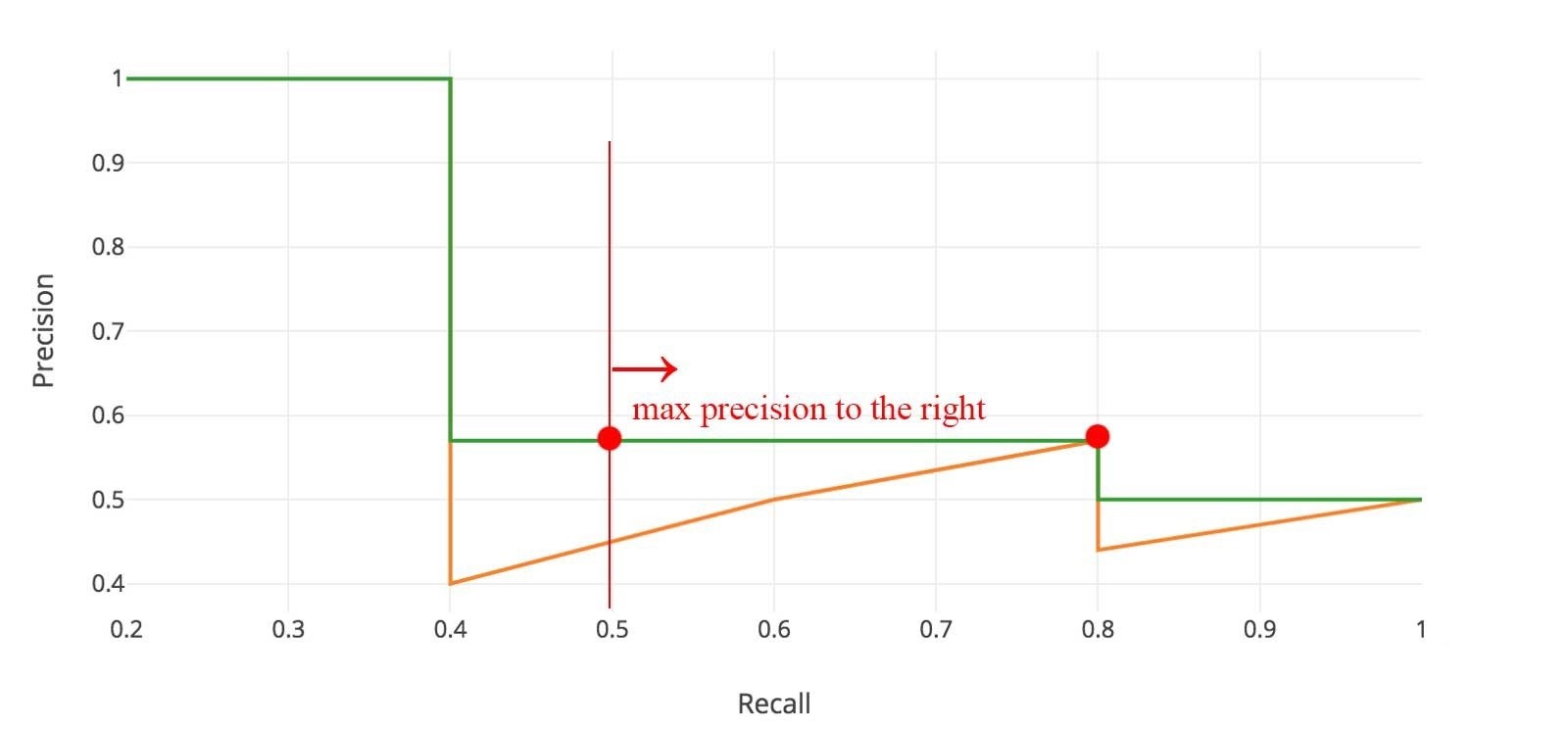
图 2 PR曲线
3. 目标检测之 YOLO算法
目前基于深度学习的目标检测算法大致可以分为两大类:两阶段 (Two-Stage) 的检测方法和一阶段 (One-Stage) 的检测方法。两阶段的检测算法比较有名的是 R-CNN, R-CNN 算法首先是通过选择性搜索 (Selective Search) 从图片中提取一定的候选区域(Region Proposal),进而在候选区域内进行分类和边界框的回归。而一阶段的检测算法比较有名的则是 YOLO, YOLO——You Only Look Once 指的则是无需提取候选区域, 而是直接通过一次端到端的神经网络,即可输出目标的位置,大小以及类别等信息。
在去掉第一个阶段的提取候选区域 (Region Proposals) 的过程后, YOLO 首先遇到的第一个问题便是如何确定边界框的数量, 而面对这个问题 YOLO 的作者 Joseph Redmon 提出了一个简单粗暴的解决方案,就是直接把图片分成 S × S 个栅格单元 (Gird Cell),每个栅格单元只会确定一个边界框 (Bonding Box)。这样做我认为至少有两个好处,首先 YOLO 算法主打的是速度,而非性能,这样的方案在大多数目标数量不算多的情况下都是可以满足要求的,而也正是因为这种方案如此的简单,因此最终也才能把检测速度提升了一个台阶:YOLOv1 的检测速度就已经可以达到 155 的 FPS,而同期的DPM 检测算法却只能达到 100 的 FPS;其次,YOLO 的这个思想也正是“分而治之” 的思想,即既然对于一整张图片难以进行直接的目标预测,那么就将其分成每一个栅格单元再进行预测,这种思想最经典的应用便是计算机的“快速排序算法”,而除此之外在多个领域上也是被认为行之有效的一个重要思想,这也正是为什么 YOLO 及其简单, 但又十分有效的原因。
3.1 YOLOv1 的检测流程
如图 3 所示,YOLOv1的检测流程如下:
(1)将所输入的图片重新调整至 448 × 448 的固定大小,具体的做法是先对图片进行等比例缩放,如果图片不是正方形尺寸的话,则再用 0 来对其边框进行填充;
(2)将 448 ×448 ×3 的矩阵送入网络中进行前向传播(预测),最终的输出是一个 7 × 7 × (2 × 5 + 20) 的矩阵,其中 7 × 7 表示 YOLOv1 将每张图片分成了 7 × 7 个栅格单元 (Gird Cell),而 2 × 5 + 20 则表示每个栅格单元 (Gird Cell) 都会预测出 2 个边界框 (Bonding Box) 和 20 个类别 (Class) 的概率,其中每个边界框又包含 5 个信息, 分别是置信度 (Confidence),边界框的中心坐标 (x, y),以及边界框的宽 w 和高 h。在这里,置信度 (Confidence) 被表示为式(3),其中如果边界框 (Bonding Box) 包含物体, 则 Pr(object) = 1;否则 Pr(object) = 0,IoU (Intersection over Union) 为预测的边界框(Bonding Box) 与物体真实区域 (Ground Truth) 的交集面积(以像素为单位,最终归一化到[0,1]),所以置信度 (Confidence) 的含义可以理解为该边界框(Bonding Box) 内包含目标且位置准确的程度。另外,中心坐标 (x, y) 也以栅格单元 (Gird Cell) 的大小归一化到[0, 1],边界框的宽 w 和高 h 则以 448 为大小归一化到 [0, 1]。
\begin{equation}\label{equ:Confidence}
Confidence = Pr(object) \times IoU_{pred}^{truth}\mbox{,} Pr(object) = \left\{
\begin{aligned}
& 1 \quad \mbox{目标在该格子里} \\
& 0 \quad \mbox{目标不在该格子里} \\
\end{aligned}
\right.
\end{equation}
(3)由于 YOLOv1 的每个栅格单元 (Gird Cell) 最终只能预测出一个边界框 (Bond- ing Box) 和一个类别 (Class) ,所以首先要将其中一个置信度 (Confidence) 较低的边界框 (Bonding Box) 的置信度 (Confidence) 置 0,同时只保留概率最高的一个类别 (Class) , 其余类别 (Class) 也置 0。但是这样一来仍然会有一个问题,就是并不能保证同一个目标不会被多个栅格单元 (Gird Cell) 所同时预测,因此这时便还要再做最后一步处理—— NMS (非极大值抑制)。NMS 的核心思想是:选择得分最高的作为输出,把与该输出重叠较高的排除掉,并不断地重复该过程直到把所有的候选对象都处理完。具体步骤如下:首先将所有预测为相同类别 (Class) 的放一起,然后用式(4)分别计算他们的得分(Score),此时还需要设置一个阈值 (Score Threshold) 来把得分 (Score) 较低的直接清除, 并最终按这个得分 (Score) 给他们排一个序,接下来便是从上到下地计算该预测出来的边界框 (Bonding Box) 与所有比其得分 (Score) 更高的边界框 (Bonding Box) 的 IOU,此时需要再设置一个阈值 (IOU Threshold) 来把所有重叠度较高的候选对象排除掉,那么最后留下来的便是这个类别 (Class) 所有可以输出的预测结果。同理,把其余的 19 个类别 (Class) 都按相同的步骤进行操作得到的便是最终结果。
\begin{equation}\label{equ:Score}
Score = P(Class_i) \times Confidence
\end{equation}

图 3 YOLOv1 的检测流程
3.2 YOLOv1 的网络结构
YOLOv1 的网络结构如图 4 所示,可以说 YOLOv1 主要是借鉴了 GooLeNet 的设计思想,包括了 24 个卷积层和 2 个全连接层,但 YOLOv1 并没有使用 Inception 模块, 而是直接使用一个 1 × 1 的卷积层和随后的 3 × 3 卷积层将其替换。
此外YOLOv1 首创性地将激活函数换成了LeakyReLU,其函数的表达式如式(5), 与 ReLU 类似,但是在输入小于 0 时,ReLU 的输出只能为 0;而 LeakyReLU 在输入小于 0 时,输出为负,且仍有微小的梯度,这样在一定程度上便解决了当输入为负时,输出始终为 0,且其一阶导数也始终为 0,神经元无法自行更新权重的“神经元死亡”问题 (Dead Neuron)。
\begin{equation}\label{equ:LeakyReLU}
f(x) = \left\{
\begin{aligned}
& x \quad & x > 0 \\
& 0.1x & Others \\
\end{aligned}
\right.
\end{equation}
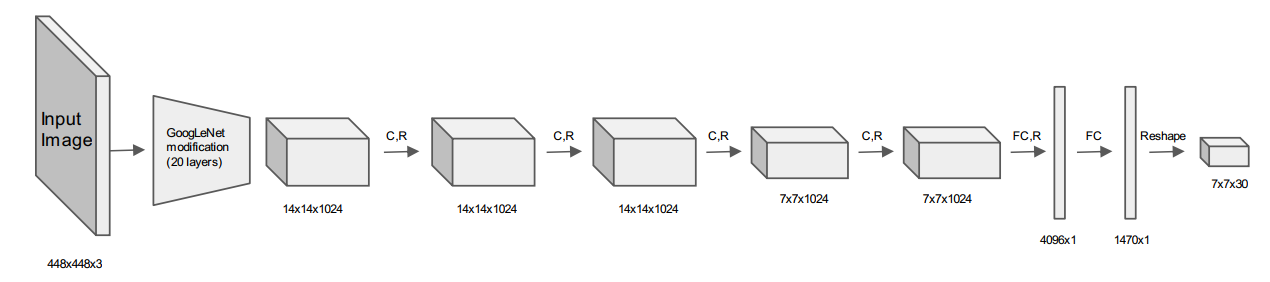
图 4 YOLOv1 的网络结构
3.3 YOLOv1 的损失函数
YOLOv1 的损失函数 (Loss Function) 如图 5 所示,包括了位置坐标误差,IoU 误差和分类误差三大部分,其中IoU 误差就是根据每个栅格单元 (Gird Cell) 所预测出来的置信度 (Confidence) 进行计算,需要注意的是置信度 (Confidence) 较低的另一个边界框(Bonding Box) 是不参与计算的。

图 5 YOLOv1 的损失函数
3.4 YOLOv2 对 YOLOv1 提出的改进
(1) 批归一化 (Batch Normalization)
在深度学习中,由于问题的复杂性,我们往往会采取较深层的网络结构来进行训练,而对于深层网络来说,当低层网络的参数发生变化时,会使得下一层的输入数据分布也发生变化,再通过层层的叠加和放大(类似于蝴蝶效应),高层网络的输入数据分布便会变化得非常剧烈,这使得高层网络需要不断地调整来重新适应低层网络所产生的参数更新,这也是为什么深层网络往往难以训练的主要原因之一。针对这一现象, Google 将其总结为 Internal Covariate Shift。此外由于大多数的激活函数,如:sigmoid 和 tanh 等都存在着梯度饱和区,因此 Internal Covariate Shift 除了会降低网络的训练速度外,还会导致网络在训练过程中容易陷入梯度饱和区,导致网络无法进一步地收敛。而针对这一问题 Google 也早在 2015 年便提出了 Batch Normalization 的方法,该方法的主要步骤是在每层的输入前都加入一个 BN 层,而 BN 层的作用就是将所有的输入数据都归一化为分布均值为 0,方差为 1 的数据,从而保证了输入数据在原有网络上的表达能力,不仅缓解了使用饱和性激活函数(如 sigmoid,tanh 等)所带来的梯度消失问题, 加快了模型的训练速度,同时还在一定程度上起到了正则化(减少模型的过拟合程度, 提高其泛化效果)的功能。最终 YOLOv2 通过引入批归一化使 mAP 提升了 2.4 个点。
(2) 高分辨率微调分类模型 (High Resolution Classifier)
由于图像分类的训练样本比较多,而标注了边框的图像检测样本则比较少,因为标注边框的人工成本比较高。所以目标检测模型通常会先用图像分类样本来训练卷积层,提取图像特征。但问题是图像分类样本的分辨率一般都不是很高,YOLOv1 在使用 ImageNet 的图像分类样本时是采用 224 × 224 来作为输入的,而在训练目标检测时, 则直接采用更高分辨率的 448 × 448 图像来作为输入,但这样的切换对模型性能肯定是会有影响的。所以 YOLOv2 在采用 224 × 224 图像进行分类模型预训练后,再采用了448 × 448 的高分辨率样本对分类模型进行微调,大概是 10 个 epoch,使网络特征逐渐适应 448 × 448 的分辨率。最后再使用 448 × 448 的检测样本进行训练,这样一来便缓解了分辨率突然切换所带来的影响了。而最终 YOLOv2 也通过此举使 mAP 提升了 3.7 个点。
(3) 采用先验框的卷积层输出 (Convolutional with Anchor Boxes)
由于与生成候选区域的网络 (Region Proposal Network) 相比 YOLOv1 在召回率 (Re-call) 明显相对较低,因此 YOLOv2 借鉴了 Faster R-CNN 的设计思想,取消了全连接层和一个池化层,直接用卷积层来作为网络的输出,同时将栅格单元 (Gird Cell) 的数量增加至 13 × 13,而输入的图片尺寸则更改为 416 × 416,这样一来便使得 YOLOv2 的网络卷积层输出有了更高的分辨率。但是栅格单元 (Gird Cell) 的数量增加了,要回归的边界框(Bonding Box) 数量也同样增加了,如果再像YOLOv1 一样,边界框(Bonding Box) 的坐标位置信息还是直接从随机的初始化数据当中回归的话,效果显然是不佳的,于是YOLOv2 同样也借鉴了Faster R-CNN 先验框(Anchor Boxes) 的思想,预先设定多组不同大小和宽高比的先验值 (Anchor),来尽可能地与最终所预测出来的目标大小和宽高比相一致,这样一来,不仅使得 YOLOv2 有了更快的回归速度,也就是加快了模型的训练速度并一定程度上提高了模型最终的训练效果,同时还解决了 YOLOv1 对于一个栅格单元 (Gird Cell) 不能同时识别多个目标的缺点,采用先验框 (Anchor Boxes) 的机制,可以使不同尺寸的目标都尽可能地往离自己更近的先验值 (Anchor) 回归。最终 YOLOv2 虽然没能通过这一改进来提高自己的 mAP,但是却把召回率 (Recall) 从原有的 81% 提高至 88%,一下子将痛点问题得以解决。
(4) 维度聚类 (Dimension Clusters)
虽然采用先验框 (Anchor Boxes) 的机制已经为 YOLOv2 争取了不少的召回率 (Re- call),但是YOLO 的作者发现有一种更好地方法可以替代手工的先验值(Anchor),那便是维度聚类 (Dimension Clusters)。YOLOv2 采用了 K 均值聚类算法(K-means Clustering Algorithm) 最终得到了 5 个 Centroid 边框,也就是 5 组先验值 (Anchor)。K-means 聚类的算法流程大致如下:预先将数据分为 K 组并随机地选取 K 个对象作为初始的聚类中心 (Centroid),然后计算每个对象与聚类中心 (Centroid) 的距离,并把每个对象分配给距离较近的聚类中心 (Centroid),最终重新计算每组的聚类中心 (Centroid),接下来要做的便是重复分配对象和计算聚类中心 (Centroid) 的这两个过程,并直至最后趋于稳定, 聚类中心 (Centroid) 不再发生变化。在这里比较重要的便是对于这个“距离”的定义, YOLO 的作者发现采用常规的欧式距离,也就是误差平方和 SSE (Sum of the Squared Errors),对于大边框会产生更大的误差,于是 YOLO 的作者想到既然我们关心的只是边框的 IoU,那何不直接采用 IoU 来定义两个边框之间的距离呢,于是在 YOLOv2 中K-means 聚类的“距离”被定义为式(6),其中 Box 就是要被分配的边框,Centroid 就是聚类时被选作中心的边框。
\begin{equation}\label{equ:Distance}
D(Box, Centroid) = 1 - IoU_{Box}^{Centroid}
\end{equation}
(5) 约束预测边框的位置 (Direct Location Prediction)
YOLO 的作者发现虽然借鉴了 Faster R-CNN 的先验框 (Anchor Boxes) 机制,但是在训练的早期阶段,模型对位置坐标的预测很不稳定,极不容易收敛,YOLO 的作者思考其原因应该是出在原本的方法并没有对边界框 (Bonding Box) 的中心坐标预测进行限制,这导致边界框 (Bonding Box) 的中心坐标可以出现在任意位置,这便失去了YOLO 原本设想的只让边界框 (Bonding Box) 的中心坐标落在该栅格单元 (Gird Cell) 中才对其进行预测的核心思想了。于是 YOLO 的作者对预测公式进行了改进,如式(7) 和图 6 所示,其中 bx, by, bw, bh 分别是边界框 (Bonding Box) 的中心坐标和宽高,而Pr(object) × IoUtruth 则是边界框 (Bonding Box) 的置信度,cx, cy 是当前网格左上角的坐标(单位是 grid ),pw, ph则是先验框 (Anchor Boxes) 的宽和高,σ则是 sigmoid函数,最后 tx, ty, tw, th, to 是模型要学习的参数,分别用于预测边界框 (Bonding Box) 的中心坐标,宽高和置信度。从公式中可以看出,边界框 (Bonding Box) 的中心坐标由于 sigmoid 函数的限制,所以被很好地约束在了栅格单元 (Gird Cell) 当中,而边界框(Bonding Box) 的高和宽采用指数函数来控制又很好地将放大和缩小平均地分配到了 0 的两侧。约束预测边框位置的方法使得模型更加容易训练,也使得预测更加稳定,最终YOLOv2 通过维度聚类和该方法的结合一下子把 mAP 又提升了 4.8 个点。
\begin{equation}\label{equ:Anchor}
\begin{aligned}
b_x & = \sigma(t_x) + c_x \\
b_y & = \sigma(t_y) + c_y \\
b_w & = p_w e^{t_w} \\
b_h & = p_h e^{t_h} \\
Pr(object) \times IoU_{pred}^{truth} & = \sigma(t_o)
\end{aligned}
\end{equation}
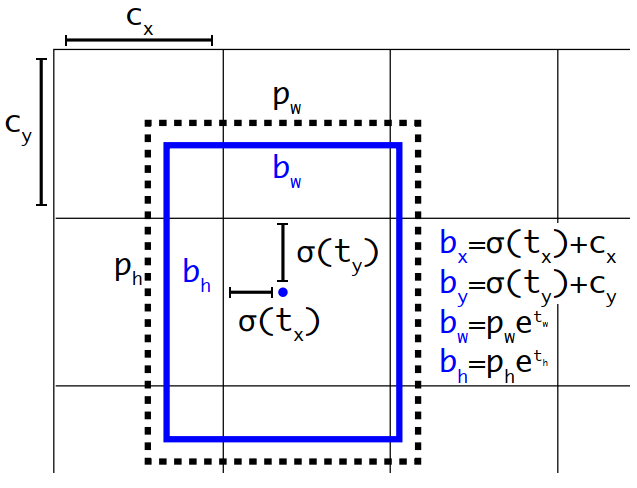
图 6 YOLOv2 基于维度聚类得到的Anchor 进行预测的边界框
(6) 细粒度特征 (Fine-Grained Features)
目标检测面临的一大困难是目标对象有大有小,很不固定,而输入图像经过多层网 络提取特征后,输出的特征图对于较小的目标来说可能已经不明显了,因此为了更好地 检测出一些较小的目标,输出的特征图需要保留更多更细节的信息,于是 YOLOv2 引入了自创的 Passthrough 层来解决这一问题。具体步骤如图 7 所示,在最后一个池化(Pooling) 层之前,特征图的大小是 26 × 26 × 512,首先将其 1 拆为 4,然后直接传递到池化 (Pooling) 层与卷积层之后与更高维的特征图进行叠加得到新的特征图 (13 × 13 × 3072)。最终 YOLOv2 通过这一做法继续将 mAP 往上提高了 1 个点。
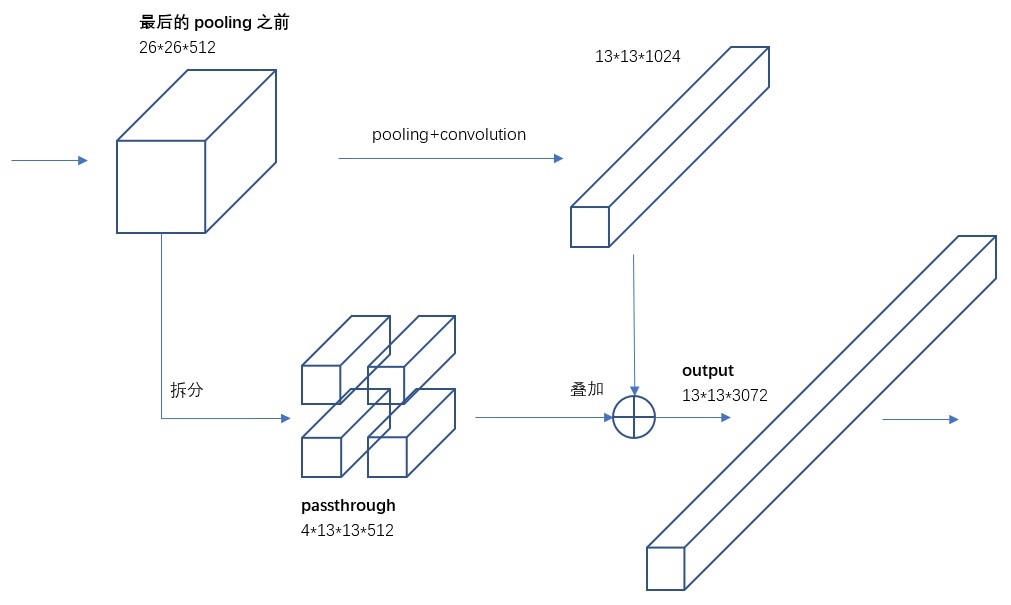
图 7 YOLOv2 Passthrough 层
(7) 多尺度图像训练 (Multi-Scale Training)
由于在第 (3) 点中已经介绍过 YOLOv2 借鉴了 Faster R-CNN 的设计思想,取消了所有的全连接层,进而替换为卷积层,除了前面所叙述的优点外,在这里还有更重要的 一个优点是可实现多尺度图像训练。对于全连接层来说,网络权重的数量是与网络输入 的数量相对应的,也就是说对于同一个模型来说,只要更改网络输入的数量,那么网络 权重的数量也要相应的进行更改,而对于单纯只由卷积层和池化层所构成的网络而言 则不存在着这样的问题,因为卷积层的参数是共享的,无论网络输入的数量如何发生改 变,网络权重的数量也可以一直保持不变。也正是因为这个原因所以 YOLO 的作者采用了 320, 352, ..., 608 等10种输入图像的尺寸进行训练(之所以要间隔 32 来选择图像的尺寸是因为网络中的下采样倍数为 32,所以一定要保证图像的尺寸为 32 的倍数,不然提取的特征图就会出现问题),在训练时每隔 10 个 batch 就随机更改一种尺寸,使网络更好地适应不同尺度的图像。最终 YOLOv2 通过该方法又把 mAP 往上提高了 1.4 个点。
(8) 高分辨率图像的目标检测 (High Resolution Detector)
由于更改了网络结构后的 YOLOv2 可以支持多种尺寸的图像输入,因此将通常使用的 416 × 416 的输入图像更换为 544 × 544 的输入图像后,又可以将 mAP 往上提高 1.8 个点,并最终将 mAP 定格于 78.6,甚至还高于同期的 Faster R-CNN: 76.4 和同样是一阶段检测的 SSD: 76.8。
3.5 YOLOv3 对 YOLOv2 提出的改进
(1)采用了新的 Darknet-53 网络。
(2)利用了多尺度特征进行目标检测。
虽然对于如何提高预测小目标的精度问题,YOLOv2 便已经提出了使用Passthrough 层来保留细粒度特征 (Fine-Grained Features) 的方法,但是在随后的 2017 年,当特征金字塔的网络结构 (Feature Pyramid Networks) 被提出之后,YOLOv2 所采用的方法显然就没那么有效了,于是 YOLOv3 也更进一步地采用 3 种不同尺度的特征图来对目标进行检测。
(3)目标分类使用了 Logistic 来替代 Softmax,从而可以支持多标签预测。
标签:Box,人脸识别,YOLOv2,YOLOv1,IoU,Bonding,原理篇,深度,边界 From: https://www.cnblogs.com/Kelvin-Wu/p/16797747.html