首页 > 其他分享 >Codeforces Round #815 (Div. 2) 题解

Codeforces Round #815 (Div. 2) 题解

时间：2022-08-20 09:55:49浏览次数：47  
标签：10 leq int 题解 oplus read while Div 815

CF1720A. Burenka Plays with Fractions

给出两个分数 $ \dfrac{a}{b}$ 和 \(\dfrac{c}{d}\) ，你每次操作能够选择其中一个分数的分子或分母，将其乘上任意一个整数（当然不能对分母乘 \(0\)）。要求求出能够使两个分数相等的最小操作次数。

分类讨论题。

考虑证明最多操作次数不超过两次：

\[\frac{a}{b}\times\Big(\frac{b}{a}\times\frac{c}{d}\Big)=\frac{a}{b}\times\frac{bc}{ad}=\frac{c}{d} \]

最多在分子分母分别乘上 \(bc,ad\) 两次。

什么时候不用乘 \(2\) 次：

  • 若 \(ad=bc\) 则为 \(0\) 次；
  • 若 \(ad=0\) 或 \(bc=0\) 或 \(ad\bmod bc=0\) 或 \(bc\bmod ad=0\) 则为 \(1\) 次；
  • 剩下皆为 \(2\) 次。
#include<bits/stdc++.h>
using namespace std;
 
#define int long long
 
inline int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){
		if(c=='-')f=-1;
		c=getchar();
	}
	while(c<='9'&&c>='0'){
		x=(x<<1)+(x<<3)+(c^48);
		c=getchar();
	}
	return x*f;
}
 
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x>9)print(x/10);
	putchar(x%10^48);
}
 
int t,a,b,c,d,x,y;
 
signed main(){
	t=read();
	while(t--){
		a=read(),b=read(),c=read(),d=read();
		x=a*d,y=b*c;
		if(x==y)puts("0");
		else if(!x||!y)puts("1");
		else if(x%y==0||y%x==0)puts("1");
		else puts("2");
	}
	return 0;
}

CF1720B. Interesting Sum

给定一个长度为 \(n\) 的序列 \(a\)，令 \(s=\max(a_1,a_2,\dots,a_{l-1},a_{r+1},\dots,a_{n-1},a_n)-\min(a_1,a_2,\dots,a_{l-1},a_{r+1},\dots,a_{n-1},a_n)+\max(a_l,a_{l+1},\dots,a_{r-1},a_r)-\min(a_l,a_{l+1},\dots,a_{r-1},a_r)\)
要求选定一个区间 \([l,r]\)，使得 \(s\) 最大，输出 \(s\)。

结论题。

  • 即为选一个区间使区间内极差加上区间外极差最大。
  • 将 \(a\) 排序，取区间 \([2,n-1]\)，答案即为 \(a[n]+a[n-1]-a[2]-a[1]\)。
#include<bits/stdc++.h>
using namespace std;
 
inline int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){
		if(c=='-')f=-1;
		c=getchar();
	}
	while(c<='9'&&c>='0'){
		x=(x<<1)+(x<<3)+(c^48);
		c=getchar();
	}
	return x*f;
}
 
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x>9)print(x/10);
	putchar(x%10^48);
}
 
const int N=1e5+5;
int t,n,a[N]; 
 
int main(){
	t=read();
	while(t--){
		n=read();
		for(int i=1;i<=n;++i)a[i]=read();
		sort(a+1,a+n+1);
		print(a[n]+a[n-1]-a[1]-a[2]),puts("");
	}
	return 0;
}

CF1720C. Corners

有一个由 0 和 1 组成的矩阵。

每次操作可以选择一个 \(2\times 2\) 的子矩阵，在这个子矩阵中选择一个 L 形，将这个 L 形里的 3 个数变成 \(0\)，注意，这个 L 形至少含有一个 1，你想最大化操作个数，问最多操作多少次。

我们最想一次操作选的 \(L\) 形中有且只有一个 \(1\)，此时答案即为 \(\sum a_i\)，我们考虑什么时候不能达到。

对一个 \(2\times 2\) 的子矩阵进行研究，发现当子矩阵中有一个 \(1\) 时，最多操作 \(1\) 次，没有浪费。

有两个 \(1\) 时，不论是斜对角还是同行同列，都可以进行两次操作，没有浪费。

有三个 \(1\) 时，只能进行两次操作，浪费了 \(1\) 次。

有四个 \(1\) 时，也只能进行两次操作，浪费了 \(2\) 次。

而当我们清空出一个 \(2\times 2\) 的子矩形时，其他所有 \(1\) 都能被 \(1\) 次操作消去，不会浪费。

统计每个子矩形中最小的浪费个数即可。

#include<bits/stdc++.h>
using namespace std;
 
inline int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){
		if(c=='-')f=-1;
		c=getchar();
	}
	while(c<='9'&&c>='0'){
		x=(x<<1)+(x<<3)+(c^48);
		c=getchar();
	}
	return x*f;
}
 
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x>9)print(x/10);
	putchar(x%10^48);
}
 
const int N=505;
int t,n,m,a[N][N],ans,minn,tmp;
char c;
 
int main(){
	t=read();
	while(t--){
		n=read(),m=read(),ans=0,minn=1e9;
		for(int i=1;i<=n;++i){
			for(int j=1;j<=m;++j){
				cin>>c;
				if(c=='1')a[i][j]=1,ans++;
				else a[i][j]=0;
			}
		}
		for(int i=1;i<n;++i){
			for(int j=1;j<m;++j){
				tmp=a[i][j]+a[i][j+1]+a[i+1][j]+a[i+1][j+1];
				if(tmp==1||tmp==2)minn=min(minn,0);
				else if(tmp==3)minn=min(minn,1);
				else minn=min(minn,2);
			}
		}
		if(!ans)puts("0");
		else print(ans-minn),puts("");
	}
	return 0;
}

CF1720D1. Xor-Subsequence (easy version)

给你一个长为 \(n\) 的整数数组 \(a_0,a_1,\dots,a_{n-1}\)。求一个最长的序列 \(b_0,b_1,\dots,b_m\) 满足：\(0\leq b_0<b_1<\dots<b_{m-1}<n\) 且 \(\forall p\in[0,m)\cap\textbf{N},a_{b_p}\oplus b_{p+1}<a_{b_{p+1}}\oplus b_p\)。输出最大的 \(m\)。

\(1\leq T\leq 10^5,2\leq n\leq 3\times 10^5,0\leq a_i\leq 200,\sum n\leq 3\times 10^5\)

有意思的题。

首先你要读懂题，读透题。

然后我们考虑 \(dp\)，记 \(f[i]\) 为以 \(i\) 为结尾的最长的 \(b\) 序列长度。

可以枚举 \(j\) 转移 \(f[i]=\max_{j<i}(f[i],f[j]+1)\)，总时间复杂度 \(O(Tn^2)\)，显然不行。

考虑不枚举 \(j\)。

发现这题的特别点：\(0\leq a_i\leq 200\)，由于异或，考虑二进制。

显然 \(a_i\) 在二进制下最多有 \(8\) 位。

分析这个式子：\(a_j\oplus i<a_i\oplus j\)，其中 \(j<i\) 为枚举的转移点。

由于 \(i>j\) 但是 \(i\) 在式子的左边，并且 \(a_i,a_j\) 又特别小，所以要想满足此式，\(i,j\) 在二进制下位数大于 \(8\) 时必须有最高位到第 \(8\) 位相等，再比较第 \(0\sim 7\) 位。

我们考虑通过此优化转移过程：

  • \(i<256\) 时，暴力转移；
  • \(i\ge 256\) 时，我们可以限定 \(j\) 的范围 \(256\times\lfloor\frac{i}{256}\rfloor\leq j<i\)，暴力转移。

这样时间复杂度就优化到了 \(O(256Tn)\)，足以通过。

#include<bits/stdc++.h>
using namespace std;
 
inline int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){
		if(c=='-')f=-1;
		c=getchar();
	}
	while(c<='9'&&c>='0'){
		x=(x<<1)+(x<<3)+(c^48);
		c=getchar();
	}
	return x*f;
}
 
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x>9)print(x/10);
	putchar(x%10^48);
}
 
const int N=3e5+5;
int t,n,a[N],f[N],ans;
 
int main(){
	t=read();
	while(t--){
		n=read(),ans=0;
		for(int i=0;i<n;++i)a[i]=read(),f[i]=1;
		for(int i=0;i<n;++i){
			if(i<256){
				for(int j=0;j<i;++j){
					if((a[j]^i)<(a[i]^j))f[i]=max(f[i],f[j]+1);
				}
			}else{
				int tmp=((i>>8)<<8); 
				for(int j=tmp;j<i;++j){
					if((a[j]^i)<(a[i]^j))f[i]=max(f[i],f[j]+1);
				}
			}
			ans=max(ans,f[i]);
		}
		print(ans),puts("");
	}
	return 0;
}

CF1720D2. Xor-Subsequence (hard version)

题意同上，\(0\leq a_i\leq 10^9\)。

我们无法再分块 \(dp\) 了。

考虑解决异或问题最常见的三种方法：按位讨论，字典树，线性基。这里考虑字典树，按位讨论。

观察这个式子 \(a_j\oplus i<a_i\oplus j\)，我们发现两者从最高位向下一直相等直到第 \(k\) 位才不同，而这个不同，一定是：\(a_j\oplus i\) 的第 \(k\) 位为 \(0\)，\(a_i\oplus j\) 的第 \(k\) 位为 \(1\)。

相等？异或虽然不能在不等式里移项，但可以在等式中移项。

所以有：从最高位到第 \(k\) 位，\(a_j\oplus i=a_i\oplus j\)，等价于 \(a_j\oplus j=a_i\oplus i\)。

列出满足\(a_j\oplus i\) 第 \(k\) 位为 \(0\)，\(a_i\oplus j\) 第 \(k\) 位为 \(1\) 的四种有关于 \(a_j,i,a_i,j\) 在第 \(k\) 位的情况：

\(a_j\) \(i\) \(a_i\) \(j\)
\(0\) \(0\) \(0\) \(1\)
\(1\) \(1\) \(0\) \(1\)
\(0\) \(0\) \(1\) \(0\)
\(1\) \(1\) \(1\) \(0\)

可以发现，\(a_i\oplus i\) 正好与 \(a_j\oplus j\) 相反，而此时正好满足 \(a_j\oplus i<a_i\oplus j\)。

结合上面两种发现，我们考虑在字典树中插入 \(a_i\oplus i\)。

我们记 \(nxt[p][0/1]\) 为节点 \(p\) 的 \(0/1\) 儿子的编号。既然想用字典树优化 \(dp\) 的转移，就要统计节点所在子树内的 \(f[j]\) 最大值，所以我们插入的时候加上一个参数 \(i\) 以便计算子树内 \(f\) 最大值。

而想要满足不等式，除了让两者相反，还必须让 \(a_i,j\) 相反，要不然第 \(k\) 位 \(a_j=1,i=0,a_i=0,j=0\) 虽然相反，却无法保证小于。

所以我们在记录节点子树内最大值时还要记录经过该点的数在这一位上的 \(0/1\) 值。

记 \(g[p][0/1]\) 为插入的 \(a_i\oplus i\) 经过 \(p\) 点后，以 \(p\) 为根，\(i\) 在此位上为 \(0/1\) 时的子树内最大 \(f\) 值。

寻找时我们将 \(a_i\oplus i\) 的第 \(k\) 位取反并且满足 \(i\) 与此点表示的 \(a_j\) 相反此位相反的 \(g\) 值取最大即可，可以看看代码。

每一次先通过字典树寻找最优的 \(j\)，再插入 \(a_i\oplus i\) 即可。

#include<bits/stdc++.h>
using namespace std;
 
inline int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){
		if(c=='-')f=-1;
		c=getchar();
	}
	while(c<='9'&&c>='0'){
		x=(x<<1)+(x<<3)+(c^48);
		c=getchar();
	}
	return x*f;
}
 
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x>9)print(x/10);
	putchar(x%10^48);
}
 
const int N=3e5+5;
int t,n,a[N],f[N],ans;
int nxt[N*31][2],g[N*31][2],cnt;
 
void insert(int x,int k){
	int p=0;
	for(int i=29;i>=0;--i){
		if(!nxt[p][x>>i&1])nxt[p][x>>i&1]=++cnt;
		p=nxt[p][x>>i&1];
		g[p][k>>i&1]=max(g[p][k>>i&1],f[k]);
	}
}
 
int find(int x,int k){
	int p=0,ans=0;
	for(int i=29;i>=0;--i){
		ans=max(ans,g[nxt[p][!(x>>i&1)]][!(k>>i&1)]);
		p=nxt[p][x>>i&1];
		if(!p)break;
	}
	return ans; 
} 
 
int main(){
	t=read();
	while(t--){
		n=read(),ans=cnt=0;
		for(int i=0;i<=n*30;++i)nxt[i][0]=nxt[i][1]=g[i][0]=g[i][1]=0;
		for(int i=0;i<n;++i)a[i]=read();
		for(int i=0;i<n;++i){
			f[i]=find(a[i]^i,a[i])+1;
			insert(a[i]^i,i);
			ans=max(ans,f[i]);
		}
		print(ans),puts("");
	}
	return 0;
}

CF1720E. Misha and Paintings

给你一个 \(n\times n\) 的矩阵 \(a\)，你可以对 \(a\) 进行任意次操作，操作的具体步骤如下：

  • 选择矩阵 \(a\) 的一个正方形子矩阵；
  • 选择一个正整数数 \(x\)，其中 \(1\leq x\leq n^2\)；
  • 将子矩阵内的所有元素修改为 \(x\)。

你需要求出使矩阵 \(a\) 恰好包含 \(k\) 个不同元素所需的最小操作次数，最小操作次数可以为 \(0\)。

\(1\leq n\leq 500,1\leq a_{i,j},k\leq n^2\)

记原始矩阵中不同值的个数为 \(m\)。

  • \(m\leq k\)

每次只要选中一个 \(1\times 1\) 的小矩阵改变值即可，最小操作次数为 \(k-m\)。

  • \(m>k\)

样例以及手玩似乎答案不超过 \(2\)？考虑证明。

我们构造出一种两次一定能解决的方案。

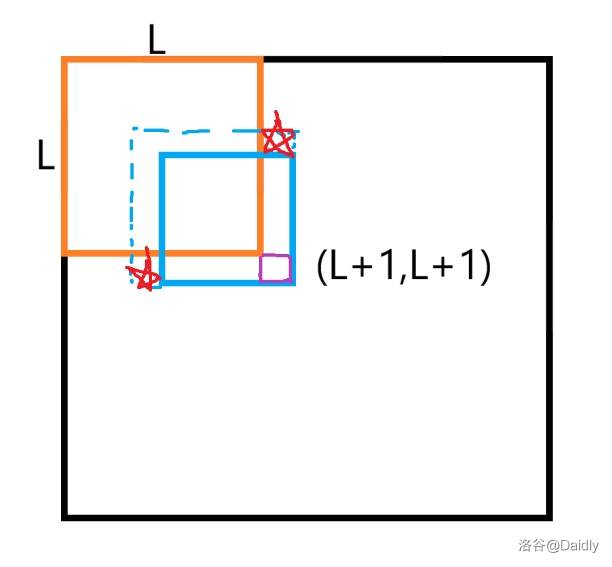
不妨让第一次选中的正方形左上角为原矩阵左上角，假设我们能增加长度 \(L\) 就增加，并且此矩形的颜色我们不统计上，即颜色为剩下 \(k\) 个之一，不增加颜色。

也就是说，我们选择了最大的 \(L\) 使得 \(m'\ge m\)，\(L\) 再增加 \(1\) 就会使 \(m'<m\)。

我们考虑第二个矩形，将它的右下角置于 \((L+1,L+1)\)，向左上扩展，颜色与第一个矩形相同，都不对整体做贡献。

可以发现，每当第二个矩形边长多 \(1\) 就会多两个格子消失，最多消失两种颜色，所以可以通过此将颜色变到 \(k\) 或 \(k-1\)。

当 \(m'=k\) 时，已满足要求；当 \(m'=k-1\) 时，我们可以将第二个矩形的颜色换成一种新的颜色，将 \(m'\) 增加 \(1\)，使其等于 \(k\)。

这样我们就证明了最多两次。

我们考虑什么时候答案为 \(1\)，其余时候都为 \(2\)。

先计算出每个颜色的上界 \((x1,y1)\)，下界 \((x2,y2)\)。即 \((x_1,y_1),(x2,y2)\) 是满足能覆盖此种颜色的最小子矩阵。

枚举一个正方形的边长 \(len\)，然后枚举左上角 \((i,j)\)，记 \(c[i][j]\) 为当边长为 \(len\) 左上角为 \((i,j)\) 时，能覆盖的颜色个数。

考虑如何计算 \(c[i][j]\)，直接算复杂度太高，考虑每个颜色的贡献。

对于一种颜色 ，通过它的上下界可以计算出在哪一个区域内的点以 \(len\) 为边长得到正方形可以覆盖这种颜色。

我们通过二维差分加二维前缀和解决 \(c\) 的计算。

最后我们只需要判断每一个点 \((i,j)\) 在长为 \(len\) 的前提下计算出的 \(m-c[i][j]\) 是否等于 \(k\) 或 \(k-1\) 即可。

\(k-1\) 是选中的矩阵颜色可以改变导致的。注意计算细节。

#include<bits/stdc++.h>
using namespace std;
 
inline int read(){
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9'){
		if(c=='-')f=-1;
		c=getchar();
	}
	while(c<='9'&&c>='0'){
		x=(x<<1)+(x<<3)+(c^48);
		c=getchar();
	}
	return x*f;
}
 
void print(int x){
	if(x<0)putchar('-'),x=-x;
	if(x>9)print(x/10);
	putchar(x%10^48);
}
 
const int N=505;
int n,k,a[N][N],c[N][N],m;
struct node{
	int x1,y1,x2,y2;
}b[N*N];
 
int main(){
	n=read(),k=read();
	for(int i=1;i<=n*n;++i)b[i].x1=b[i].y1=1e9;
	for(int i=1;i<=n;++i){
		for(int j=1;j<=n;++j){
			a[i][j]=read();
			b[a[i][j]].x1=min(b[a[i][j]].x1,i);
			b[a[i][j]].y1=min(b[a[i][j]].y1,j);
			b[a[i][j]].x2=max(b[a[i][j]].x2,i);
			b[a[i][j]].y2=max(b[a[i][j]].y2,j);
		}
	}
	for(int i=1;i<=n*n;++i)if(b[i].x1!=1e9)m++;
	if(m<=k){print(k-m);return 0;}
	for(int len=1;len<=n;++len){
		memset(c,0,sizeof(c));
		for(int i=1;i<=n*n;++i){
			if(b[i].x1==1e9)continue;
			int X1=max(1,b[i].x2-len+1);
			int Y1=max(1,b[i].y2-len+1);
			int X2=min(n-len+1,b[i].x1);
			int Y2=min(n-len+1,b[i].y1);
			if(X1<=X2&&Y1<=Y2){
				c[X1][Y1]++;
				c[X2+1][Y1]--;
				c[X1][Y2+1]--;
				c[X2+1][Y2+1]++;
			}
		}
		for(int i=1;i<=n;++i){
			for(int j=1;j<=n;++j){
				c[i][j]+=c[i-1][j]+c[i][j-1]-c[i-1][j-1];
				if(m-c[i][j]==k||m-c[i][j]==k-1){
					puts("1");return 0;
				}
			}
		}
	}
	puts("2");
    return 0;
}
  • 总结：冷静读题，观察特殊点。

完结撒花！

标签：10,leq,int,题解,oplus,read,while,Div,815
From： https://www.cnblogs.com/Daidly/p/16607199.html

相关文章

  • 2022 牛客多校 Extra & 第九场部分题解
    2022牛客多校第九场&Extra部分题解前段时间沉迷生活大爆炸&原神&vtb&galgame&番无法自拔，因此咕到现在。。。Cmostp挺妙的题。本以为有一只log的做法。......
  • 题解CF94B Friends
    简洁题意：求出任三点之间是否存在直接连通或都不连通，若存在，输出WIN，否则输出FAIL由于数据范围非常小，m<=10,则我们可以采用暴力枚举三个点的方式求出答案#include<bit......
  • Codeforces Round #815 (Div. 2) D2 Xor-Subsequence (hard version)
    原题链接\(A>B\)，总是有二进制下从高到低的前\(k\)位相等，第\(k+1\)位\(A\)是\(1\)，\(B\)是\(0\)本题中\(A=a_i\oplusj\)，\(B=a_j\oplusi\)，这里有一个很奇妙的性质（手玩或者......
  • Interesting Sum - 题解【思维】
    InterestingSum-题解【思维】前言在vscode上配置了markdown插件，取代了之前写md的工具，本博客用来测试插件好不好用，所以选的题比较简单。但是jiangly这道题被FST了【滑......
  • VirtualBox 找不到桥接网卡问题解决
    1、选择下面驱动2、就可以选择了......
  • 基础数论专题题解集（暂未全部AC）
    A-青蛙的约会题面两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上，于是它们约定各自朝西跳，直到碰面为止。可是它......
  • CF Round 815 Div2 题解
    A题BurenkaPlayswithFractions（签到）给定2个分数\(\dfrac{a}{b},\dfrac{c}{d}\)，现在可以自行进行操作，每次选定一个分数，将其分子或者分母乘上一个数，问至少需要多少次......
  • Codeforces #815 Div.2
    A—BurenkaPlayswithFractions思路：数论O(1)见题解题解：#include<iostream>#include<cstring>#include<algorithm>usingnamespacestd;typedeflonglongL......
  • 嘿嘿，天城大人嘿嘿嘿——苍与红的试炼 题解
    苍与红的试炼嘿嘿天城大人，嘿嘿天城大人您要怎么蹂躏我嘿嘿。众所周知，我是老指挥官了，所以看到这道题异常兴奋。然而我发现这道题好像是改编题，网上找不到题解，怎么能冷落天......
  • 状压DP-1815. 得到新鲜甜甜圈的最多组数
    问题描述有一个甜甜圈商店，每批次都烤 batchSize 个甜甜圈。这个店铺有个规则，就是在烤一批新的甜甜圈时，之前所有 甜甜圈都必须已经全部销售完毕。给你一个整数batchSi......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99