需要一些trick的一场
H: 2 -sat的板子,已经计入2-sat专题,此处不再详细描述。题目用矩阵包装和博弈包装,我们需要慢慢读题,分析样例,找到问题的关键点。
G:题意:给定一个数组,数组中任何两个数异或<4的数对可以交换位置 ,可以交换无限次,求能够形成的字典序最小的数组。
Sol:我们希望能够快速将能够交换的数对都聚集在一起,然后内部排个序,再按顺序送回每个位置上,时间复杂度\(O(nlogn)\)。所以我们只需要思考两个数怎么样才能异或起来<4,那么显然应该二进制位下分析,我们发现只需要高29位一样,剩的低三位随便怎么样我们不在乎,也就是说这样的数共有的特征是x>>2都是一样的,所以我们直接map<int,vector>存一下每个数,再对于每个vector排序.又由于不想存下标,所以我们只能倒着做回去利用vector的pop_back功能
void solve(){
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
map<int,vector<int>>mp;
for(int i=1;i<=n;i++){
int u=a[i]>>2;
mp[u].push_back(a[i]);
}
for(auto &[x,y]:mp){
sort(y.begin(),y.end());
}
for(int i=n;i>=1;i--){
int u=a[i]>>2;
a[i]=mp[u].back();
mp[u].pop_back();
}
for(int i=1;i<=n;i++)cout<<a[i]<<" ";
cout<<endl;
}
F: 题意:给定整数 \(r\) ,求与 \((0, 0)\) 的欧氏距离大于或等于 \(r\)但严格小于 \(r+1\)的格点个数。大于或等于 \(r\) ,但严格小于 \(r+1\) 的网格点的个数。
网格点是具有整数坐标的点。从 \((0, 0)\) 到点 \((x,y)\) 的欧氏距离为 \(\sqrt{x^2 + y^2}\)。
Sol:敢于枚举,特判边界。四个象限我们只需要计算一个就可以了,计算第一象限,我们考虑枚举横坐标,直接计算与两个圆的交点,从而计算有多少个纵坐标符合要求。对于开方操作,注意其下取整的特性,对于上下边界都有不同的处理,自己看看题目要求想想。
void solve(){
cin>>n;
int ans=0;
for(int i=1;i<=n;i++){
int low=n*n-i*i;
low=sqrt(low);
if(low*low<(n*n-i*i))low++;
int up=(n+1)*(n+1)-i*i;
up=sqrt(up);
if(up*up==((n+1)*(n+1)-i*i))up--;
ans+=max(0LL,up-low+1);
}
ans*=4;
cout<<ans<<endl;
}
E:普通二分+物理简单计算。然而机器翻译round down翻译四舍五入,但实际上应该下取整,导致早早的陷入浮点数误差。现在我们知道不需要四舍五入了,但计算过程中速度是小数,我们不希望出现引入它,我们就应该把整个数学公式写出来然后变形,只做最后一次下取整的除法。
//原来根本不用浮点数,就是下取整除法
void solve(){
int k;cin>>n>>k>>m;
vector<int>a(k+1,0);
vector<int>b(k+1,0);
set<int>pos;pos.insert(0);
for(int i=1;i<=k;i++){
cin>>a[i];pos.insert(a[i]);
}
map<int,int>mp;mp[0]=0;
for(int i=1;i<=k;i++){
cin>>b[i];
mp[a[i]]=b[i];
}
for(int i=1;i<=m;i++){
int x;cin>>x;
// bug(x);
if(mp.count(x)){
cout<<mp[x]<<" ";
}
else {
auto r=pos.lower_bound(x);
auto l=r;
l--;
//bug(*l);bug(*r);
int res=mp[*l];
int dx=(*r)-(*l);
int dt=mp[*r]-mp[*l];
int tt=(x-*l)*dt/dx;
//bug(res);
res+=tt;
//bug(res);
baoliu(res,0);cout<<" ";
//bug(ans);
}
}
cout<<endl;
}
D:从思路正确到越跑越远,到最后wa5次。
题意:给你一个二进制字符串 s 。请找出最少需要切割成多少个片段,以便将得到的片段重新排列成一个有序的二进制字符串。
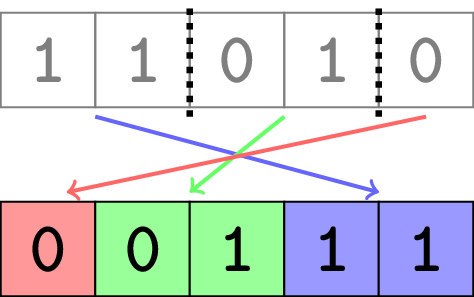
请注意
- 每个字符必须正好位于其中一个片段中;
- 片段必须是原始字符串的连续子串;
- 在重新排列时必须使用所有片段。
\(^{\dagger}\) 二进制字符串是由字符 \(\texttt{0}\) 和 \(\texttt{1}\) 组成的字符串。排序后的二进制字符串是指所有字符 \(\texttt{0}\) 都位于所有字符 \(\texttt{1}\)之前的二进制字符串。
考虑最终答案形态:只有一个交界处会是01,其他情况邻居都是和自己一样的,所以我们考虑只要和右边不一样就切割,切割n次,再判断一下有没有01段,得到切割ans次,则答案是ans+1段
void solve(){
string s;cin>>s;
bool flag=0;int cnt=0;
for(int i=0;i<s.size()-1;i++){
cnt+=(s[i]!=s[i+1]);
if(s[i]=='0'&&s[i+1]=='1')flag=true;
}
cout<<(cnt+1-flag)<<endl;
}