P7903 兜心の顶
题目背景
Source:八仙敬酒
- 吕洞宾——醉酒提壶力千钧;
- 铁拐李——旋肘膝撞醉还真;
- 汉钟离——跌步抱坛兜心顶;
- 蓝采和——单提敬酒拦腰破;
- 张果老——醉酒抛杯踢连环;
- 曹国舅——仙人敬酒锁喉扣;
- 韩湘子——擒腕击胸醉吹箫;
- 何仙姑——弹腰献酒醉荡步。
题目描述
给定正整数 \(n\),要求构造一棵 \(n\) 个结点的树,满足树的直径的重心 不是 树的重心。
同时这棵树需满足:直径\(^1\)、重心\(^2\)、直径的重心\(^3\)全部唯一。
注:
- 树的直径\(^1\):https://oi-wiki.org/graph/tree-diameter/
- 树的重心\(^2\):https://oi-wiki.org/graph/tree-centroid/
- 树的直径的重心\(^3\):将树的直径(一条链)视作一棵树,求其重心(一个点)。
输入格式
第一行输入一个正整数 \(n\),表示树的结点个数。
输出格式
第一行输出一个正整数 \(n\)。
接下来 \(n-1\) 行,每行输出两个正整数 \(u,v\),表示树的一条边。
无解输出 -1。
本题采取 Special Judge,输出任意一组合法解均给分。
样例 #1
样例输入 #1
20
样例输出 #1
20
20 18
1 3
19 12
19 4
16 1
4 1
1 7
16 10
7 20
13 8
10 2
18 13
13 17
14 18
11 19
16 5
2 6
16 9
17 15
样例 #2
样例输入 #2
2
样例输出 #2
-1
提示
样例说明
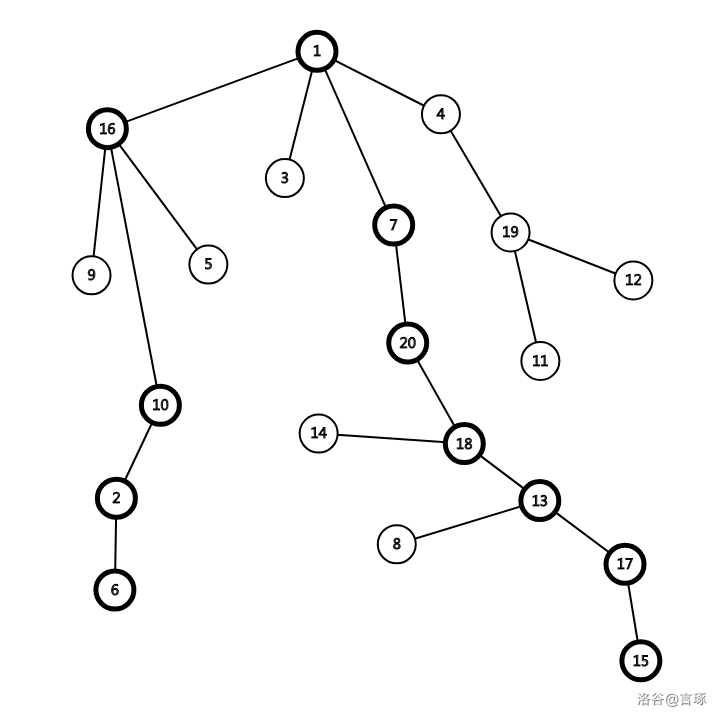
样例 #1 中直径的重心是 \(7\),树的重心是 \(1\),\(1\ne7\)。
样例 #2 中 \(n=2\),只有两个点时显然重心不可能唯一。
数据范围
本题采取捆绑测试。
| 子任务编号 | 分值 | 特殊性质 |
|---|---|---|
| \(1\) | \(30\) | \(n\le10\) |
| \(2\) | \(30\) | \(n\) 是奇数 |
| \(3\) | \(30\) | \(n\) 是偶数 |
| \(4\) | \(10\) | 无 |
对于 \(100\%\) 的数据:\(1\le n\le10^4\)。
题目大意
构造一棵\(n\)个节点的树,使得树的直径、树的重心、树的直径的重心唯一,并且树的重心与树的直径的重心不同。
分析
我们先构造一个长链作为树的直径,
由于树的直径的重心唯一,
显然 直径应为奇数。
分情况讨论
-
显然直径长度为\(1\)时不满足题意。 -
当直径长度为\(3\)时:
此时,树的直径的重心为\(点2\)。
若要 “满足树的直径的重心不是树的重心” ,那么树的重心可供选取的位置为\(点1\)或\(点3\)。
当然,这两个位置是等价的假如我们选\(点1\):
那么为了让
她\(点1\) 成为重心,我们至少要给 \(点1\) 一个节点……吗?
细看可发现:此时树的重心有\(点1\),\(点2\)两个重心,
所以我们至少要给\(点1\) 两个节点。
当然,此时树的直径变为了\(4\),不满足题意。
-
当直径长度为\(5\)时:
此时,树的直径的重心为\(点3\)。
那么现在树的重心可供选取的位置为\(点1\)(\(\Leftrightarrow 点5\))或\(点2\)(\(\Leftrightarrow 点4\))。
当我们选\(点1\)时,与直径长度为\(3\)时同理。当我们选\(点2\)时,我们可以在此节点上增加至少两个节点(同上)使他成为树的重心。

乂~ 多了两个直径 咋办呢?
在\(点1\)上再加一个点不就完事了嘛~

乂~ 直径成偶数了 咋办呢?
为了不让树的直径的重心与树的重心重合,我们只能在\(点5\)再加一个节点。
最终我们得到了一个完整的大保健 一颗兜心の顶树,ta的直径为\(7\),重心为\(点2\),直径的重心为\(点3\)。

综上,\(n \leq 8\)时 无解。
乂~ 那如果点数比\(8\)多 咋办呢?
其实有些熟悉毒瘤题的dalao可能已经想到了,这实际上就是一个菊花图。
给\(点3\)疯狂加点不就完了嘛~

Elaina's code
Elaina's code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define Elaina 0
inline int read(){
int x=0,f=1;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
return x*f;
}
int n;
main(){
n=read();
if(n<=8) return printf("-1"),Elaina;
printf("%lld\n",n);
printf("1 2\n");
printf("2 3\n");
printf("3 4\n");
printf("4 5\n");
printf("5 6\n");
printf("6 7\n");
for(int i=8;i<=n;++i){
printf("3 %lld\n",i);
}
return Elaina;
}