MaHengbo-2022-MultiObjectiveDiverseHumanPredictionWithKnewledgeDistillation

标签：tau right boldsymbol MaHengbo 2022 MultiObjectiveDiverseHumanPredictionWithKnewl

Multi-Objective Diverse Human Motion Prediction With Knowledge Distillation #paper

---

1. paper-info

1.1 Metadata

• Author:: [[Hengbo Ma]], [[Jiachen Li]], [[Ramtin Hosseini]], [[Masayoshi Tomizuka]], [[Chiho Choi]]
• 作者机构::
• Keywords:: #HMP
• Journal:: #CVPR
• Date:: [[2022]]
• 状态:: #Doing

• 链接:: https://openaccess.thecvf.com/content/CVPR2022/html/Ma_Multi-Objective_Diverse_Human_Motion_Prediction_With_Knowledge_Distillation_CVPR_2022_paper.html

1.2 Abstract

Obtaining accurate and diverse human motion prediction is essential to many industrial applications, especially robotics and autonomous driving. Recent research has explored several techniques to enhance diversity and maintain the accuracy of human motion prediction at the same time. However, most of them need to define a combined loss, such as the weighted sum of accuracy loss and diversity loss, and then decide their weights as hyperparameters before training. In this work, we aim to design a prediction framework that can balance the accuracy sampling and diversity sampling during the testing phase. In order to achieve this target, we propose a multi-objective conditional variational inference prediction model. We also propose a short-term oracle to encourage the prediction framework to explore more diverse future motions. We evaluate the performance of our proposed approach on two standard human motion datasets. The experiment results show that our approach is effective and on a par with state-of-the-art performance in terms of accuracy and diversity.

---

2. Introduction

• 领域： Human motion prediction
• generative model 的问题：

Otherwise, even if we assume that the generative models can capture the actual data distribution, the data distribution can still be very imbalanced and skewed, which makes that sampling the minor modes is challenging within a limited number of samples.

• 已有的多样化动作生成模型的问题：
  • It implies that such approaches cannot be adjusted and controlled during the testing phase.
• 本文方法：
  • multi-objective conditional variational autoencoder: 可以在测试阶段，控制生成多样化动作和精确动作序列之前的比例。
  • short-term oracle system:
    • We propose to learn a short-term oracle system and distill the oracle’s knowledge into the prediction framework to increase the diversity of human future motions. In order to achieve this goal, we propose a novel sample-based loss to supervise the predictor during the training phase.

3. Methodology

3.1 符号

• \(\mathcal{D}\): dataset
• 用时间范围来表示动作序列。\(T = T_h + T_f\) ,\(T_h\)表示历史动作序列的时间；\(T_f\)表示待预测的时间段。
• \(X_{t-T_h+1:t+T_f}=[X_{t-T_h+1,...,X_{t+T_f}}]\):动作序列，包括历史序列和待预测序列。
• \(C = X_{t-T_h+1:t}\)：历史动作序列。
• \(P(X_{t+1:t+T_f}|C,\rho )\) ：待预测动作序列的条件概率分布。\(\rho \in [0, 1]\)：用于控制多样化的参数。
• \(X^i_{t+1:t+T_f} \sim P(X_{t+1:t+T_f}|C,\rho )；i=1,....,M\) ：\(M\)表示采样的个数。

3.2 Multi-Objective Predictor

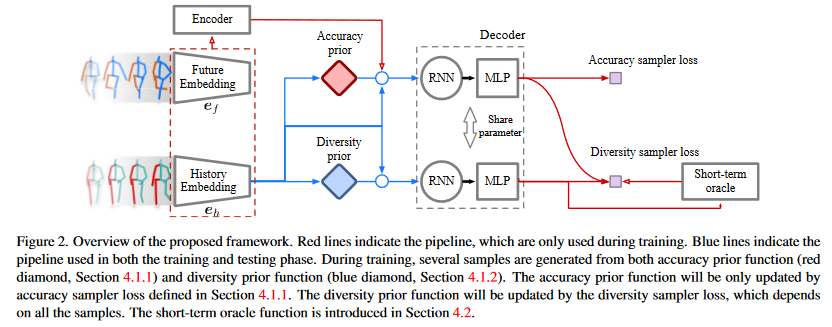
Figure 1. Overview of the proposed framwork
Source: https://openaccess.thecvf.com/content/CVPR2022/html/Ma_Multi-Objective_Diverse_Human_Motion_Prediction_With_Knowledge_Distillation_CVPR_2022_paper.html

latent variable model：

\[P(X|C,Q)=E_{Z\sim Q(Z|C)}[P(X|C,Z)] \]

作者提出了两种latent code的先验分布：

• \(Q_{acc}(Z|C)\)：该先验分布用于生成准确的动作序列。
• \(Q_{div}(Z|C)\)：该先验分布用于生成多样化的动作序列。
  并且，作者提出了两个encoder, 如Figure 1的红色虚线框。(注意：红色实线流程只在训练的时候使用)
• historical observation encoder\(e_h(C)\)
• future information encoder\(e_f(X)\)

\[\begin{array}{l} \mathrm{e}_{\boldsymbol{h}}(\boldsymbol{C})=[\mathrm{MLP} \circ \mathrm{RNN}](\boldsymbol{C}) \\ \mathrm{e}_{\boldsymbol{f}}(\boldsymbol{X})=[\mathrm{MLP} \circ \mathrm{RNN}](\boldsymbol{X}), \end{array} \]

3.2.1 Accuracy Sampler

accuracy sampler只用于优化\(Q_{acc}(Z|C)\)。和变分推理一样，最大化evidence lower bound(ELBO)

\[\begin{array}{c} \mathcal{L}_{\text {ELBO }}=\mathbb{E}_{Q_{\psi}(\boldsymbol{Z} \mid \boldsymbol{X}, \boldsymbol{C})}\left[\log P_{\theta}(\boldsymbol{X} \mid \boldsymbol{Z}, \boldsymbol{C})\right] \\ -D_{K L}\left[Q_{\psi}(\boldsymbol{Z} \mid \boldsymbol{X}, \boldsymbol{C}) \| Q_{\mathrm{acc}}(\boldsymbol{Z} \mid \boldsymbol{C})\right] \end{array} \]

变分推理假设\(Z \in N(0, I)\)， 但是实验证明各项独立的正态高斯分布不能够很好地学习到数据中的复杂的多模态数据分布。于是作者用普通的高斯分布代替：\(Q_{acc}(Z|C) \in N(\mu _{\phi _{acc}}(C), \sum_{\phi _{acc}}(C))\) ，由于没有对\(Z\)的先验控制，训练难度会上升，为了防止无法训练，加入了正则化项：

\[\begin{aligned} \mathcal{R}_{\mathrm{acc}} &=\min _{i}\left\|\hat{\boldsymbol{X}}^{i}-\boldsymbol{X}\right\|^{2} \\ z^{i} & \sim Q(\boldsymbol{Z} \mid \boldsymbol{C}) \\ \hat{\boldsymbol{X}}^{i} &=\mathrm{d}_{0}\left(\boldsymbol{X} \mid \boldsymbol{C}, z^{i}\right), i=1, \ldots, n_{\mathrm{acc}} \end{aligned} \]

$n_{acc}$：表示采样的数目。于是`accuracy sampler `的`overall loss function`为：

\[\mathcal{L}_A(\theta, \phi) = -\lambda_{ELBO} \mathcal{L}_{\text {ELBO }} + \lambda_{acc}\mathcal{R}_{\mathrm{acc}} \]

3.2 Diversity Sampler

Diversity loss function:

\[\begin{array}{l} \operatorname{DIV}(\mathcal{X}, \mathcal{Y})=\frac{1}{N_{x} N_{y}} \sum_{i, j} e^{-d\left(\boldsymbol{X}^{i}, \boldsymbol{Y}^{j}\right)} \\ \boldsymbol{X}^{i}, \boldsymbol{Y}^{j} \in \mathcal{X}, \mathcal{Y}, i=1, \ldots, N_{x}, j=1, \ldots, N_{y} \end{array} \]

\(\mathcal{X}\)和\(\mathcal{Y}\)表示两个不同的采样集；\(d(x,y)=\eta \left \| x-y \right \|_2\)
作者定义的diversity loss function：

\[\mathcal{L}_{div}=\alpha_{div}DIV(\mathcal{X}_{div}, \mathcal{X}_{div})+(1-\alpha_{div})DIV(\mathcal{X}_{div},\mathcal{X}_{acc}) \]

只使用\(DIV(\mathcal{X}_{div},\mathcal{X}_{acc})\)只能够控制多样性与精确性之间的差异，但是不能控制生成的动作序列是符合现实的，很有可能生成错误的动作，为了控制生成的动作序列符合正常规律，假设存在未来序列的分布：

\[\tilde{X}_{t+1:t+\tau }\in \mathcal{O}(X_t, \tau) \]

The oracle \(\mathcal{O}\) can be seen as a teacher to distill the “knowledge”

基于这个\(oracle \mathcal{O}\) ，作者定义了a sample-based loss：

\[\begin{array}{c} \mathcal{L}_{\mathrm{ref}}(\tau)=\frac{1}{n_{\mathrm{div}}} \sum_{i, s} \min _{j}\left\|\hat{\boldsymbol{X}}_{s \tau+1:(s+1) \tau}^{i}-\tilde{\boldsymbol{X}}_{s \tau+1:(s+1) \tau)}^{j}\right\|^{2}, \\ \text { s.t. } \boldsymbol{z}^{i} \sim Q_{\mathrm{div}}(\boldsymbol{Z} \mid \boldsymbol{C}), \hat{\boldsymbol{X}}_{1: T}^{i}=\mathrm{d}_{\theta}\left(\boldsymbol{X} \mid \boldsymbol{C}, \boldsymbol{z}^{i}\right), \\ \tilde{\boldsymbol{X}}_{s \tau+1:(s+1) \tau}^{j} \sim \mathcal{O}\left(\hat{\boldsymbol{X}}_{s \tau}, \tau\right), \\ \quad i=1, \ldots, n_{\mathrm{div}}, j=1, \ldots, n_{0}, s=0, \ldots, T / \tau-1, \end{array} \]

\(\tau\)：预言机预测姿势的时间间隔
\(n_{div}\)：通过diversity prior采样出的样本数量
\(n_o\)：从oracle中采样的样本数量

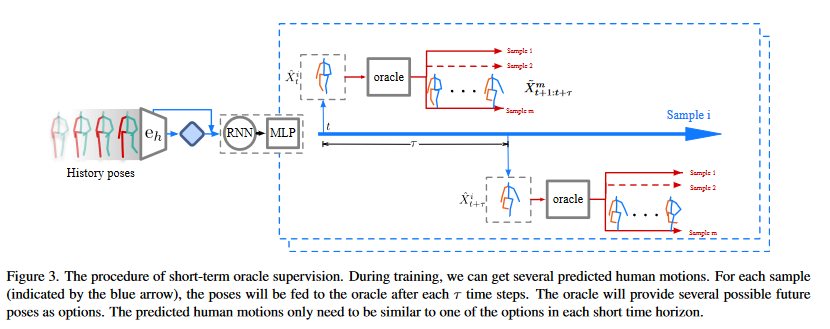
Figure 2. The procedure of short-term oracle supervision
Source: https://openaccess.thecvf.com/content/CVPR2022/html/Ma_Multi-Objective_Diverse_Human_Motion_Prediction_With_Knowledge_Distillation_CVPR_2022_paper.html

同时作者加入了很常用的physical feasibility losses

\[\mathcal{L}_{phy}=\lambda \mathcal{L}_{vel} + \mathcal{L}_{limb} \]

\(\mathcal{L}_{vel}\)：对速度的限制

\[\mathcal{L}_{\mathrm{vel}}(\boldsymbol{X})=\frac{1}{T} \sum_{t-0}^{T-1}\left\|\boldsymbol{X}_{t+1}-\boldsymbol{X}_{t}\right\|^{2} \]

\(\mathcal{L}_{limb}\)：对关节的限制

\[\mathcal{L}_{\text {limb }}(\boldsymbol{X})=-\lambda_{\text {dir }} \log P(\boldsymbol{n})+\frac{\lambda_{\text {len }}}{n_{l} T} \sum_{i} \sum_{t}\left(\left\|\hat{\boldsymbol{l}}_{i}(t)\right\|-\left\|\boldsymbol{l}_{i}\right\|\right)^{2} \]

Figure 5. 公式说明
Source:

最终的diversity sample loss:

\[\mathcal{L}_D = \lambda_{ref}\mathcal{L}_{ref} + \lambda_{div}\mathcal{L}_{div}+\mathcal{L}_{phy} \]

4. Short-term Oracle Design

通过另外一个条件变分自编码去学习pseudo-ground-truth multi-modality
定义：

\[\begin{array}{l} \Omega\left(\boldsymbol{X}_{t}\right)=\mathbf{S}\left(\mathcal{X}_{\mathrm{o}} ; \tau, K\right) \\ \mathcal{X}_{\mathrm{o}}=\left\{\boldsymbol{X}_{t+1: t+\tau}^{1} \ldots \boldsymbol{X}_{t+1: t+\tau}^{\left|\mathcal{X}_{\mathrm{o}}\right|}\right\} \\ d\left(\boldsymbol{X}_{t}^{j}, \boldsymbol{X}_{t}\right) \leq \delta, \forall j=1, \ldots,\left|\mathcal{X}_{\mathrm{o}}\right| \end{array} \]

\(\tau\)：时间范围
\(\mathcal{X}_o\) ：表示所有的未来姿势的集合
\(\Omega(\boldsymbol{X}_{t})\)：表示在\(\tau\)和\(\mathcal{X}_o\)的条件下选择的K个未来动作序列的集合。
在选择出的未来动作序列中，相似性很高，为了捕捉不同的模型分布，作者采用了k-Determinantal point process(KDPP)，选择策略\(\mathcal{S}\)

4.1 k-Determinantal Point Process

\[\operatorname{Pr}(\mathcal{S})=\frac{\operatorname{det}\left(L_{\mathcal{S}}\right) \mathbf{1}(|\mathcal{S}|=k)}{\sum_{\mathcal{S} \subset[n],|\mathcal{S}|-k} \operatorname{det}\left(L_{\mathcal{S}}\right)}, \]

\(\mathcal{S}\) ：\(\mathcal{X}\)的子集
\(L_S \in \mathcal{R}^{|S|x|S|}\)： 相似矩阵

\[\left\{L_{\mathcal{S}}\right\}_{i j}=e^{-d\left(X_{t+1: t+\tau}^{i}, X_{t+1: t+\tau}^{j}\right)} \]

4.2 Short-term Oracle Model

---

5. Training and Testing Process

• Training

Figure 3. Training Procedure
Source: https://openaccess.thecvf.com/content/CVPR2022/html/Ma_Multi-Objective_Diverse_Human_Motion_Prediction_With_Knowledge_Distillation_CVPR_2022_paper.html

• testing

Figure 4. Testing Procedure
Source: https://openaccess.thecvf.com/content/CVPR2022/html/Ma_Multi-Objective_Diverse_Human_Motion_Prediction_With_Knowledge_Distillation_CVPR_2022_paper.html

6. Experiments

• dataset:
  • Human3.6M
  • HumanEva-I
• Evaluation Metrics
  • Average Displacement Error(ADE)
  • Final Displacement Error(FDE)
  • Average Pairwise Distance(APD)

---

7. 总结

和Dlow模型类似，也是对潜在变量进行变换，DLow是在一个预训练模型上重新学习潜在变量；而该方法利用了两种潜在变量，用于分别控制精确度和多样性。在生成多样性动作序列的过程中，一方面要注意多样性，一方面要注意生成动作序列的合理性。作者加入了一个未来序列预测机，用于控制生成的序列的合理性。
在我看来，这些生成多样性动作序列的方法都是利用一种新框架来生成动作序列，但是框架不是精度和多样性的关键，关键在于损失函数的设计。(用于控制多样性和动作序列的合理性)

• Limitations and Future work
  • 加入graph neural network去提高预测精度。
  • 提高动作序列的顺滑度。
  • 考虑动作序列的语义\上下文信息
  • 新的多模态指标

---

标签：tau,right,boldsymbol,MaHengbo,2022,MultiObjectiveDiverseHumanPredictionWithKnewl
From： https://www.cnblogs.com/guixu/p/16798988.html