以下设 \(\operatorname{dis}(x,y)\) 表示树上 \(x,y\) 两点间的距离。修改时对 \(u\) 的周围与 \(u\) 距离小于等于 \(d\) 的点的点权乘 \(w\)。
暴力不行,于是考虑打标记。
注意到 \(0\le d\le 40\),一个很自然的想法是:设 \(tag(x,i)\) 表示将 \(x\) 的子树内与 \(x\) 距离小于等于 \(i\) 的所有点的点权乘 \(tag(x,i)\)。修改时遍历 \(l\) 分别表示 \(u\)、\(u\) 的父亲……\(u\) 的 \(d\) 级祖先,将 \(tag(l,d-\operatorname{dis}(u,l))\) 都乘上 \(w\) 即可。查询时依然遍历 \(l\),沿途把标记累乘即可。这样 \(l\) 最多 \(O(d)\) 个取值,总复杂度是 \(O(nd)\) 的。
显然这样会有点权被重复乘 \(w\),解决方案也很简单,打标记时将重复的用除法抵消。具体的,设 \(l\) 的一个孩子 \(s\),使 \(s\) 的子树内有 \(u\),打标记时将 \(tag(s,d-\operatorname{dis}(u,l)-1)\) 即 \(tag(s,d-\operatorname{dis}(u,s)-2)\) 除以 \(w\) 即可。
下图给出了一个例子帮助理解:
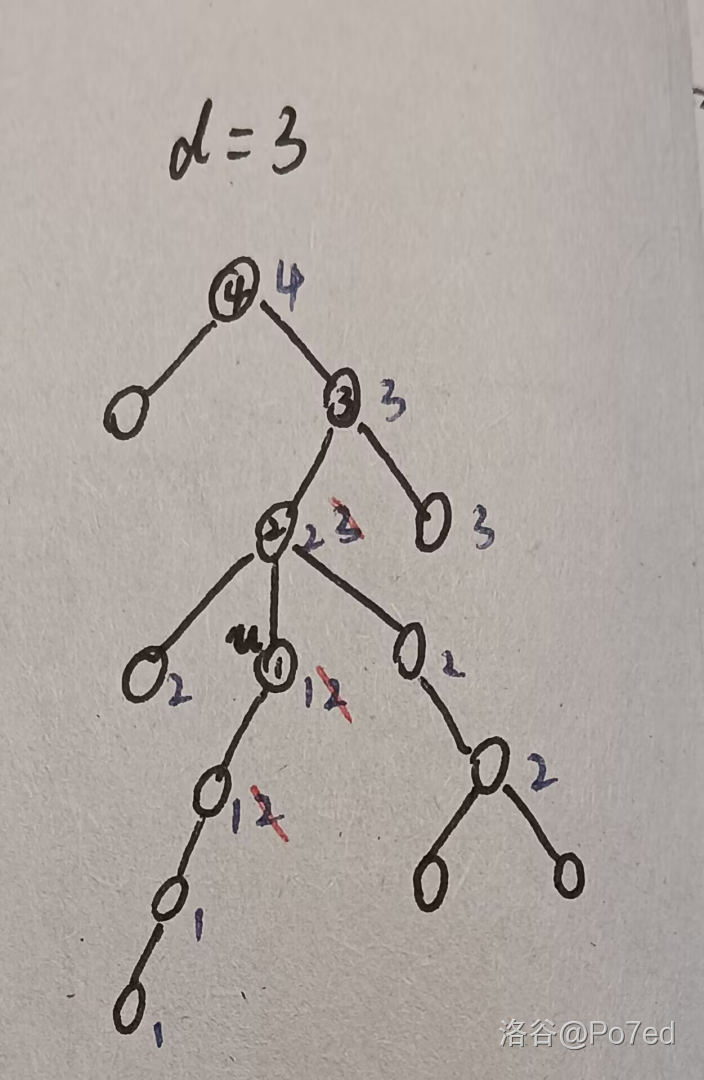
图中 \(1\) 号点(即 \(u\))将
但模数可能没有逆元,这样做还是不行
标签:标记,题解,JOISC2022,tag,P9527,operatorname,dis From: https://www.cnblogs.com/chargedcreeper/p/18175662/k-neighbor_mdf