容斥原理

容斥原理：

容斥原理是一种在知道所有集合之间的交，求集合之间的并的数学方法。（注：交即为两个集合之间相同的部分，记作 \(|A| \cap |B|\) ）

problem：

设 \(U\) 中元素有 \(n\) 种不同的属性，而第 \(i\) 种属性称为 \(P_i\)，拥有属性 \(P_i\) 的元素构成集合 \(S_i\)，现在请求出 \(U\) 中有哪些元素。

易知：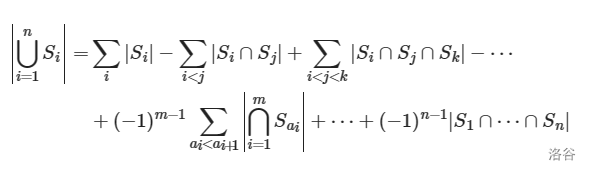

也就是：

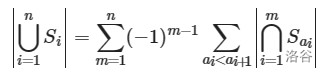
（摘自 OI-Wiki）

不定方程非负整数解计数：

problem:

给定 \(n\) 个变量，第 \(i\) 个记作 \(x_i\)。对于 \(x_i\) 有限制 \(x_i \le a_i\) 。且对于所有 \(x\) ，有 \(x_1+x_2+...+x_n=m\) ，问有多少组解。

solution:(by OI-Wiki)

对于这个问题，我们可以抽象出一个容斥模型：

1.全集：$\sum ^n_{i=1}x_i=m $ 解的个数。

2.集合：\(S_i=x_i\)

3.属性：即为限制条件。

解即为 $|\bigcap ^n_{i=1} S_i| $

我们可以通过求这个解集的补集，并用全集减去补集即可。

易知解集的补集为：\(|\bigcup^n_{i=1} !S_i|\)（不会补集怎么打） 使用插板法+容斥原理即可。

例题

贴个代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;

const int mod=1e9+7;

int n,m,a[50],ans;
int inv(int x);
int c_zh(int x,int y);

signed main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int s=1;s<=(1<<n)-1;s++){
		int cnt=0,sum=0;
		for(int i=0;i<n;i++){
			if(s&(1<<i)){
				sum+=a[n-i]+1;
				cnt++;
			}
		}
		int f=-1;
		if(cnt&1)f=1;
		ans=(ans+f*c_zh(n-1,m-sum-1+n)%mod+mod)%mod;//这里是因为将限制减掉后变成了 0 ，所以还要加上n。
	}
	cout<<(c_zh(n-1,m-1+n)%mod-ans%mod+mod)%mod<<endl;
	return 0;
}
int fast_pow(int x,int y){
	int ret=x%mod,res=1;
	while(y){
		if(y&1)res*=ret;
		ret*=ret;
		res%=mod;ret%=mod;
		y>>=1;
	}
	return res;
}
int inv(int x){
	return fast_pow(x,mod-2);
}
int c_zh(int x,int y){
    if(y<0)return 0;
	int res=1;
	for(int i=1;i<=x;i++){
		res=(res*((y-i+1)%mod))%mod;// 注意这个可能溢出
	}
	for(int i=1;i<=x;i++){
		res=(res*inv(i))%mod;
	}
	//cout<<"x: "<<x<<" y: "<<y<<" ans: "<<res<<endl;
	return res;
}

错位排列：

problem：对于一个有 \(n\) 个元素的排列 \(P\) ，如果对于所有 \(i \le n\) , 都有 \(p_i \ne i\)，则说排列 \(P\) 是一个错位排列。问对于有 \(n\) 个元素的序列有多少个错排列。

solution:

还是考虑使用全集 - 补集的方法去求解。

模型：

1.全集：\(n\) 个元素的排列：\(n!\)

2.集合：\(P_i\)

3.属性：\(P_i \ne i\)

那么很容易发现 \(P_i\) 的补集 \(U_i\) 即为满足 \(P_i=i\) 的一种解集。

所以答案即为:

\(n!-|\bigcup ^n_{i=1}U_i|\)

通过容斥原理以及组合数的定义，我们可以知道答案为（这里不再推式子）：

\(n!\sum^n_{i=0}\frac{(-1)^i}{i!}\)