第一次 VP 比赛(也是第一次打 CF)。
感到自己距离退役又近了一步。
A. Stair, Peak, or Neither?
题意
You are given three digits \(a\), \(b\), and \(c\). Determine whether they form a stair, a peak, or neither.
- A stair satisfies the condition \(a<b<c\).
- A peak satisfies the condition \(a<b>c\).
给你三个数字 \(a\) 、\(b\) 和 \(c\) 。请判断它们是形成阶梯、峰值,还是两者都不形成。
- 阶梯满足条件 \(a<b<c\) 。
- 峰值满足条件 \(a<b>c\) 。
简单模拟题。
code
#include<iostream>
#include<cstdio>
using namespace std;
int T;
int a,b,c;
void solve(){
cin>>a>>b>>c;
if(a<b&&b<c)cout<<"STAIR"<<'\n';
else if(b>a&&b>c)cout<<"PEAK"<<'\n';
else cout<<"NONE"<<'\n';
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin>>T;
while(T--)solve();
return 0;
}
//coder:Iictiw
//date:24/04/16
//When I wrote a piece of code, her and I knew what it was doing
B. Upscaling
题意
You are given an integer \(n\). Output a \(2n \times 2n\) checkerboard made of \(2 \times 2\) squares alternating '\(\texttt{#}\)' and '\(\texttt{.}\)', with the top-left cell being '\(\texttt{#}\)'.
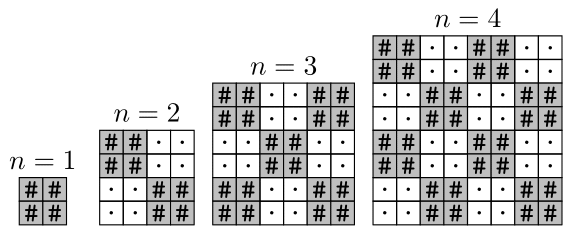
The picture above shows the answers for \(n=1,2,3,4\).
给你一个整数 \(n\) 。输出一个由 \(2 \times 2\) 个方格组成的 \(2n \times 2n\) 棋盘,其中" \(\texttt{#}\) "和" \(\texttt{.}\) "交替出现,左上角的方格为" \(\texttt{#}\) "。

上图是 \(n=1,2,3,4\) 的答案。
同样是简单模拟题。
code
#include<iostream>
#include<cstdio>
using namespace std;
int T,n;
void solve(){
cin>>n;
for(int i=1;i<=n*2;i++){
for(int j=1;j<=n*2;j++){
if(((i-1)/2+(j-1)/2)&1)cout<<'.';
else cout<<'#';
}
cout<<'\n';
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin>>T;
while(T--)solve();
return 0;
}
//coder:Iictiw
//date:24/04/16
//When I wrote a piece of code, her and I knew what it was doing
C. Clock Conversion
题意
Given the time in 24-hour format, output the equivalent time in 12-hour format.
- 24-hour format divides the day into 24 hours from \(00\) to \(23\), each of which has 60 minutes from \(00\) to \(59\).
- 12-hour format divides the day into two halves: the first half is \(\mathrm{AM}\), and the second half is \(\mathrm{PM}\). In each half, the hours are numbered in the order \(12, 01, 02, 03, \dots, 11\). Each hour has 60 minutes numbered from \(00\) to \(59\).
给出 24 小时制的时间,输出 12 小时制的相应时间。
- 24 小时格式 将一天分为 24 小时,从 \(00\) 到 \(23\) ,每个小时有 60 分钟,从 \(00\) 到 \(59\) 。
- 12 小时格式 将一天分为两半:上半部分是 \(\mathrm{AM}\) ,下半部分是 \(\mathrm{PM}\) 。在每一半中,小时按 \(12, 01, 02, 03, \dots, 11\) 的顺序编号。每个小时有 60 分钟,从 \(00\) 到 \(59\) 。
简单模拟题。
code
#include<cstdio>
int T;
int h,m;
void solve(){
scanf("%d:%d",&h,&m);
if(h>12)printf("%02d:%02d PM\n",h-12,m);
else if(h==12)printf("%02d:%02d PM\n",h,m);
else if(h==0)printf("%02d:%02d AM\n",12,m);
else printf("%02d:%02d AM\n",h,m);
}
int main(){
scanf("%d",&T);
while(T--)solve();
return 0;
}
//coder:Iictiw
//date:24/04/16
//When I wrote a piece of code, her and I knew what it was doing
D. Product of Binary Decimals
题意
Let's call a number a binary decimal if it is a positive integer and all digits in its decimal notation are either \(0\) or \(1\). For example, \(1\,010\,111\) is a binary decimal, while \(10\,201\) and \(787\,788\) are not.
Given a number \(n\), you are asked whether or not it is possible to represent \(n\) as a product of some (not necessarily distinct) binary decimals.
如果一个数是正整数,且其十进制符号中的所有数字都是 \(0\) 或 \(1\) ,我们就称它为二进制十进制数。例如, \(1\,010\,111\) 是二进制十进制数,而 \(10\,201\) 和 \(787\,788\) 不是。
给定一个数 \(n\) ,问你是否可以将 \(n\) 表示为一些(不一定不同的)二进制十进制数的乘积。
因为 \(n\) 很小,所以不大于 \(n\) 的二进制十进制数数量很少,可以直接枚举出来,然后用一个类似于埃式筛的东西把满足条件的数筛出来。
code
#include<iostream>
#include<cstdio>
using namespace std;
const int N=1e5+5;
int T,n;
int a[N],tot;
int t[N],top;
bool vis[N];
void init(int n){
for(int i=1;tot<=35;i++){
int j=i,x=0;top=0;
while(j)t[++top]=j&1,j>>=1;
while(top)x=x*10+t[top--];
a[++tot]=x;
}
vis[1]=1;
for(int i=1;i<=n;i++)
if(vis[i])
for(int j=1;j<=tot&&(long long)a[j]*i<=n;j++)
vis[a[j]*i]=1;
}
void solve(){
cin>>n;
if(vis[n])cout<<"YES"<<'\n';
else cout<<"NO"<<'\n';
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
init(1e5);
cin>>T;
while(T--)solve();
return 0;
}
//coder:Iictiw
//date:24/04/16
//When I wrote a piece of code, her and I knew what it was doing
E. Nearly Shortest Repeating Substring
You are given a string \(s\) of length \(n\) consisting of lowercase Latin characters. Find the length of the shortest string \(k\) such that several (possibly one) copies of \(k\) can be concatenated together to form a string with the same length as \(s\) and, at most, one different character.
More formally, find the length of the shortest string \(k\) such that \(c = \underbrace{k + \cdots + k}_{x\rm\ \text{times}}\) for some positive integer \(x\), strings \(s\) and \(c\) has the same length and \(c_i \neq s_i\) for at most one \(i\) (i.e. there exist \(0\) or \(1\) such positions).
给你一个长度为 \(n\) 的字符串 \(s\) ,它由小写拉丁字符组成。求最短字符串 \(k\) 的长度,使得多个(可能是一个) \(k\) 可以连接在一起,形成一个长度与 \(s\) 相同的字符串,且最多只有一个不同的字符。
更正式地说,求最短字符串 \(k\) 的长度,使得 \(c = \underbrace{k + \cdots + k}_{x\rm\ \text{times}}\) 为某个正整数 \(x\) ,字符串 \(s\) 和 \(c\) 的长度相同,且 \(c_i \neq s_i\) 中最多有一个 \(i\) 。(即存在 \(0\) 或 \(1\) 这样的位置)。
我怕不是 baka 吧,这么简单的题都想不出来,狠狠的降智了。
首先显然要枚举 \(k\) 的长度,显然这会是 \(n\) 的因数。
设长度为 \(len , s1 = s[0,len - 1] , s2= s[len,2 len -1]\) 。
由于最多有一位不同,所以如果合法,则 \(s\) 要么由 \(s1\) 拼接而成,要么由 \(s2\) 拼接而成。
直接暴力枚举就好。
code
#include<iostream>
#include<cstdio>
using namespace std;
const int N=2e5+5;
int T,n;
string s;
void solve(){
cin>>n>>s;
for(int i=1;i<n;i++){
if(n%i)continue;
string s1=s.substr(0,i),s2=s.substr(i,i);
int cnt1=0,cnt2=0;
for(int j=0,k=0;j<n;j++,k++){
if(k==i)k=0;
if(s[j]!=s1[k])cnt1++;
if(s[j]!=s2[k])cnt2++;
}
if(cnt1<=1||cnt2<=1)return cout<<i<<'\n',void();
}
cout<<n<<'\n';
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin>>T;
while(T--)solve();
return 0;
}
//coder:Iictiw
//date:24/04/16
//When I wrote a piece of code, her and I knew what it was doing
F. 0, 1, 2, Tree!
Find the minimum height of a rooted tree\(^{\dagger}\) with \(a+b+c\) vertices that satisfies the following conditions:
- \(a\) vertices have exactly \(2\) children,
- \(b\) vertices have exactly \(1\) child, and
- \(c\) vertices have exactly \(0\) children.
If no such tree exists, you should report it.
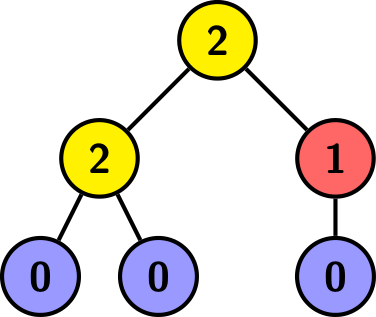
The tree above is rooted at the top vertex, and each vertex is labeled with the number of children it has. Here \(a=2\), \(b=1\), \(c=3\), and the height is \(2\).
\(^{\dagger}\) A rooted tree is a connected graph without cycles, with a special vertex called the root. In a rooted tree, among any two vertices connected by an edge, one vertex is a parent (the one closer to the root), and the other one is a child.
The distance between two vertices in a tree is the number of edges in the shortest path between them. The height of a rooted tree is the maximum distance from a vertex to the root.
求一棵有 \(a+b+c\) 个顶点的有根树 \(^{\dagger}\) 的最小高度,它必须满足以下条件:
- \(a\) 个顶点正好有 \(2\) 个子顶点、
- \(b\) 个顶点正好有 \(1\) 个子顶点,且
- \(c\) 个顶点正好有 \(0\) 个子顶点。
如果不存在这样的树,您应该报告它。

上面的树以顶点为根,每个顶点都标有子顶点的数量。这里是 \(a=2\) 、 \(b=1\) 、 \(c=3\) ,高度是 \(2\) 。
\(^{\dagger}\) 有根树是一个没有环的连通图,有一个特殊的顶点叫做根。在有根树中,由边连接的任意两个顶点中,一个顶点是父顶点(离根较近的顶点),另一个顶点是子顶点。
树中两个顶点之间的距离就是它们之间最短路径的边数。有根树的高度是顶点到根的最大距离。
目前贪心能力与DP能力不相上下,都做不出来1700(
首先特判掉 \(2a + b + 1 \neq a + b + c\) 的情况(即 \(a + 1 \neq c\)),易知这种情况无解,其他情况都有解。
其次,如果 \(a = 0\),那树高显然为 \(b\)。
其他情况应当贪心地填,将 \(a\) 类节点尽可能往上填,不够再补 \(b\) 类,先将完全二叉树补满,再往下面一排一排插。
code
#include<iostream>
#include<cstdio>
using namespace std;
int T;
int a,b,c;
void solve(){
cin>>a>>b>>c;
if(a*2+b+1!=a+b+c)return cout<<-1<<'\n',void();
if(a==0)return cout<<b<<'\n',void();
int res=1,t;
for(int x=1;;a-=x,x<<=1,res++)
if(a<=x){
t=a*2+(x-a);
b-=x-a;
break;
}
if(b<=0)cout<<res<<'\n';
else cout<<res+(b+t-1)/t<<'\n';
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin>>T;
while(T--)solve();
return 0;
}
//coder:Iictiw
//date:24/04/16
//When I wrote a piece of code, her and I knew what it was doing
G. Shuffling Songs
题意
Vladislav has a playlist consisting of \(n\) songs, numbered from \(1\) to \(n\). Song \(i\) has genre \(g_i\) and writer \(w_i\). He wants to make a playlist in such a way that every pair of adjacent songs either have the same writer or are from the same genre (or both). He calls such a playlist exciting. Both \(g_i\) and \(w_i\) are strings of length no more than \(10^4\).
It might not always be possible to make an exciting playlist using all the songs, so the shuffling process occurs in two steps. First, some amount (possibly zero) of the songs are removed, and then the remaining songs in the playlist are rearranged to make it exciting.
Since Vladislav doesn't like when songs get removed from his playlist, he wants the making playlist to perform as few removals as possible. Help him find the minimum number of removals that need to be performed in order to be able to rearrange the rest of the songs to make the playlist exciting.
弗拉迪斯拉夫的播放列表由 \(n\) 首歌曲组成,编号从 \(1\) 到 \(n\) 。歌曲 \(i\) 的流派为 \(g_i\) ,作者为 \(w_i\) 。他希望制作的播放列表中,每对相邻的歌曲要么作者相同,要么流派相同(或两者皆有)。他把这样的播放列表称为令人兴奋的播放列表。 \(g_i\) 和 \(w_i\) 都是长度不超过 \(10^4\) 的字符串。
要制作一个令人兴奋的播放列表,不一定能使用所有的歌曲,因此洗牌过程分为两步。首先,删除一定量(可能为零)的歌曲,然后重新排列播放列表中剩余的歌曲,使其更加精彩。
由于弗拉迪斯拉夫不喜欢播放列表中的歌曲被移除,因此他希望制作的播放列表能尽可能少地移除歌曲。帮助他找出需要执行的最少移除次数,以便能够重新排列剩余的歌曲,使播放列表变得精彩。
\(1 \leq n \leq 16\)
我也就会打些板题了。
先将可以放在一起的歌连边。
可以留下的歌的数量就是总点数减去最长链点数。
\(n\) 很小,果断状压。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=17;
int T;
int n;
string a[N],b[N];
bool d[N][N];
int f[N][1<<N];
void solve(){
cin>>n;
for(int i=0;i<n;i++)
cin>>a[i]>>b[i];
memset(d,0,sizeof(d));
memset(f,0,sizeof(f));
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if(a[i]==a[j]||b[i]==b[j])d[i][j]=1;
for(int i=0;i<n;i++)
f[i][1<<i]=1;
for(int S=0;S<(1<<n);S++)
for(int i=0;i<n;i++)
if((S>>i)&1){
for(int j=0;j<n;j++)
if(d[i][j]&&i!=j&&(S>>j)&1){
f[j][S]=max(f[j][S],f[i][S^(1<<j)]+1);
}
}
int ans=0;
for(int S=0;S<(1<<n);S++)
for(int i=0;i<n;i++)
ans=max(ans,f[i][S]);
cout<<n-ans<<'\n';
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin>>T;
while(T--)solve();
return 0;
}
//coder:Iictiw
//date:24/04/16
//When I wrote a piece of code, her and I knew what it was doing