P1303 A*B Problem
题目
给出两个非负整数,求它们的乘积。
输入
输入共两行,每行一个非负整数。
输出
输出一个非负整数表示乘积。
样例
输入
1
2
输出
2
提示
每个非负整数不超过 \(10^{2000}\)。
思路
根据题意,乘数的数据最大范围是 \(10^{2000}\),需要使用高精度乘高精度的算法。将每个乘数以字符串读取并倒序存储在整型数组中,参考竖式乘法运算的过程进行计算。
设两个乘数分别为 \(a_3a_2a_1\) 和 \(b_2b_1\),可以得到以下竖式
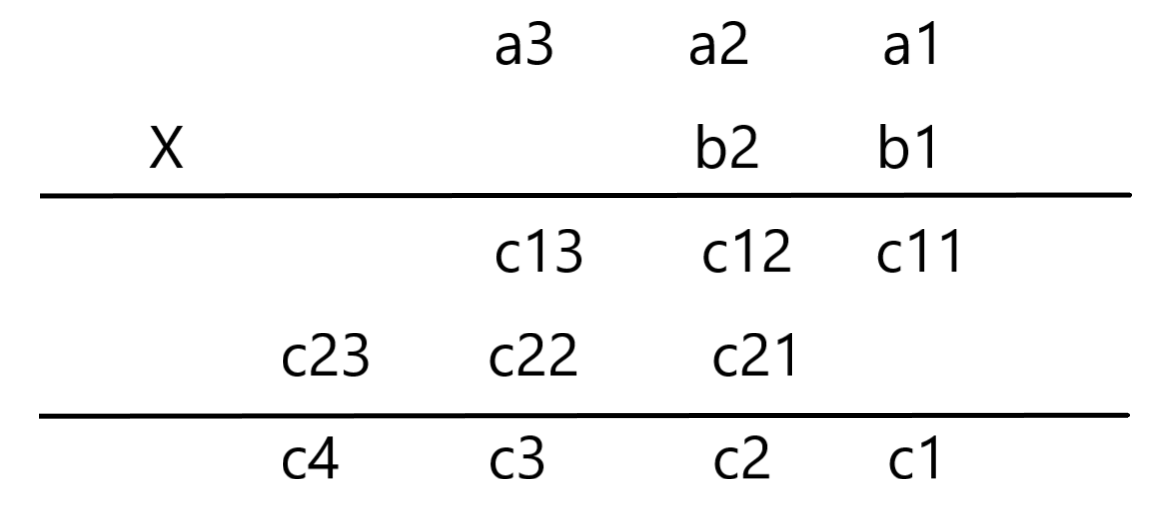
其中:
\[c_{11}=b_1 \times a_1,c_{12} = b_1 \times a_2,c_{13}=b_1 \times a_3 \]\[c_{21}=b_2 \times a_1,c_{22}=b_2 \times a_2,c_{23}=b_2 \times a_3 \]\[c_1=c_{11},c_2=c_{12}+c_{21},c_3=c_{13}+c_{22},c_4=c_{23} \]做完乘法后可以总结出规律:乘积第 \((i+j-1)\) 位的值为 \(c_{i+j-1}=\)“\((\sum (a_i \times b_j))/10+\)进位”,其中 \(1 \le i \le lena,1 \le j \le lenb\);乘积位 \(c_{i+j-1}\) 计算后大于等于 \(10\),则向 \(c_{i+j}\) 进位,\(c_{i+j-1}\) 位留下除以 \(10\) 的余数;乘积的长度最大值为 \(lena\) 与 \(lenb\) 的和,另外在乘积输出前需要将前导零去掉。
for (int i = 1; i <= lena; i ++ )
{
x = 0;
for (int j = 1; j <= lenb; j ++ )
{
x = a[i] * b[j] + x / 10 + c[i + j - 1];
c[i + j - 1] = x % 10;
}
c[i + lenb] = x / 10;
}
lenc = lena + lenb;
while (c[lenc] == 0 && lenc > 1) // 去掉多余的前导 0
lenc --;
代码一
#include <bits/stdc++.h>
using namespace std;
char a1[2010], b1[2010];
int a[2010], b[2010], c[4000010], lena, lenb, lenc, x;
void read()
{
scanf("%s %s", a1, b1);
lena = strlen(a1);
lenb = strlen(b1);
for (int i = 0; i <= lena - 1; i ++ )
a[lena - i] = a1[i] - 48;
for (int i = 0; i <= lenb - 1; i ++ )
b[lenb - i] = b1[i] - 48;
}
void mul()
{
for (int i = 1; i <= lena; i ++ )
{
x = 0;
for (int j = 1; j <= lenb; j ++ )
{
x = a[i] * b[j] + x / 10 + c[i + j - 1];
c[i + j - 1] = x % 10;
}
c[i + lenb] = x / 10;
}
lenc = lena + lenb;
while (c[lenc] == 0 && lenc > 1) // 去掉前导 0
lenc --;
}
void print()
{
for (int i = lenc; i >= 1; i -- )
cout << c[i];
}
int main()
{
read();
mul();
print();
return 0;
}
代码二:重载运算符
#include <bits/stdc++.h>
using namespace std;
char str[2010];
struct node
{
int len, s[4010];
node()
{
len = 0;
memset(s, 0, sizeof(s));
}
};
node operator * (const node &a, const node &b)
{
node c;
c.len = a.len + b.len - 1;
if ((a.len == 1 && a.s[1] == 0) || (b.len == 1 && b.s[1] == 0))
{
c.len = 1;
c.s[1] = 0;
return c;
}
for (int i = 1; i <= a.len; i ++ )
{
for (int j = 1; j <= b.len; j ++ )
{
c.s[i + j - 1] += a.s[i] * b.s[j];
c.s[i + j] += c.s[i + j - 1] / 10;
c.s[i + j - 1] %= 10;
}
}
if (c.s[c.len + 1])
{
int x = c.s[c.len + 1], len = c.len;
while (x)
{
c.s[++ len] = x % 10;
x /= 10;
}
c.len = len;
}
return c;
}
node read()
{
scanf("%s", str);
int len = strlen(str);
node a;
a.len = len;
for (int i = 0; i < len; i ++ )
a.s[len - i] = str[i] - '0';
return a;
}
void print(node a)
{
for (int i = a.len; i >= 1; i -- )
printf("%d", a.s[i]);
}
int main()
{
node a, b, c;
a = read();
b = read();
c = a * b;
print(c);
return 0;
}