0.什么是自动机
1.实现原理
\(TRIE + KMP\),详细戳这里
这里重点看代码实现
#include<bits/stdc++.h>
#define N 1000005
using namespace std;
int T,n;
char s[N],t[N];//模式串、文本串
namespace AC
{
int tot;
int tr[N][27];//字典树(图) ,u ->i-> tr[u][i] i是字母的编号
int rev[N];//对应的编号,主要是应对重复串:把重复了的第j个串对应的编号赋成前面出现过的第i个串
int fail[N], idx[N], in[N], vis[N], ans[N];
//点u的 fail指针、是第几个串的结尾、(fail指针的)入度 答案数组 插入时被字符串"经过"的次数
void init()
{
memset(tr,0,sizeof(tr));
memset(fail,0,sizeof(fail));
memset(idx,0,sizeof(idx));
memset(in,0,sizeof(in));
memset(vis,0,sizeof(vis));
memset(ans,0,sizeof(ans));
memset(rev,0,sizeof(rev));//初始化(可能会T(doge))
tot = 1;//根节点编号为1,后续节点编号从2开始
}
void insert(char x[],int id)//建字典树
{
int u = 1;
int l = strlen(x + 1);
for(int i = 1;i <= l;i++)
{
if(!tr[u][x[i] - 'a']) tr[u][x[i] - 'a'] = ++tot;
u = tr[u][x[i] - 'a'];
}
if(!idx[u]) idx[u] = id;//记录首次以u结尾的串的编号
rev[id] = idx[u];//处理重复串,当前第id个串重了的话对应的就是第idx[u]个串
return;
}
queue<int> q;
void build()//拓扑排序优化用fail指针建字典图
{
for(int i = 0;i < 26;i++) tr[0][i] = 1;
q.push(1);
fail[1] = 0;//从根开始
while(!q.empty())
{
int u = q.front();
q.pop();
for(int i = 0;i < 26;i++)
{
int v = tr[u][i];
if(!v)
{
tr[u][i] = tr[fail[u]][i];//后面没了直接拿fail当新边
continue;
}
fail[v] = tr[fail[u]][i];//KMP思想,把v的指针指入tr[fail[u]][i]
in[tr[fail[u]][i]]++;//对应上一行,tr[fail[u]][i]的指针入度增加了一个fail[v]
//cout << in[tr[fail[u]][i]] << endl;
q.push(v);
}
}
}
void topo()//拓扑搞答案
{
for(int i = 1;i <= tot;i++)
if(!in[i]) q.push(i);//拓扑套路
while(!q.empty())
{
int u = q.front();
q.pop();
vis[idx[u]] = ans[u];
int v = fail[u];
ans[v] += ans[u];//合并点的答案
in[v]--;
if(!in[v]) q.push(v);
}
}
void query(char x[])
{
int u = 1,len = strlen(x + 1);
for(int i = 1;i <= len;i++) u = tr[u][x[i] - 'a'],ans[u]++;//更新ans数组
}
void getans()
{
int sum = 0;
for(int i = 1;i <= n;i++) printf("%d\n",vis[rev[i]]);
}
}
int main()
{
scanf("%d",&n);
AC::init();
for(int i = 1;i <= n;i++) scanf("%s",s + 1),AC::insert(s,i);
AC::build();
scanf("%s",t + 1);
AC::query(t);
AC::topo();
AC::getans();
return 0;
}
对应的是板子题
2,应用
纯自动机
P3966 [TJOI2013] 单词
开始没看懂题
结合英文写作常识才知道文章是(样例为例)
\[a aa aaa \]有空格隔开的不能算做一个单词
那是不是就这样每输入一个单词就加个空格来生成文本串最后再统一与模式串(单词)匹配即可?
按理来说是这样的,得到了\(90pts\)(模拟空格的是"{",即ASCII表中z的后一个字符)
后来才发现这样做文本串会膨胀到\(10^6 + 200\),还得多开个\(200\)多的空间
#define N 1005005//内存开大
...
void init(char x[])
{
int l = strlen(x + 1);
for(int i = 1;i <= l;i++) t[++cnt] = x[i];
t[++cnt] = '{';
}
...
//剩下的都是上道题的板子
P5231 [JSOI2012] 玄武密码
这里要求的是最长前缀,本来想着只靠\(TRIE\)也行,后来发现缺的要素太多,比如当前匹配不上要记录长度时该把答案归到哪个模式串头上,同时沿着树向下进行类\(dfs\)操作时不把答案记乱的一些细节等等
那我们不妨利用下\(AC\)自动机里的成分
这里,\(fail\)指针成为一个利器,因为结合含义,他可以用来记录哪些前缀(不一定最长)出现在了文本串中(\(fail\)可能跨串,如下图,也可能像\(KMP\)一样在同串之间跳)
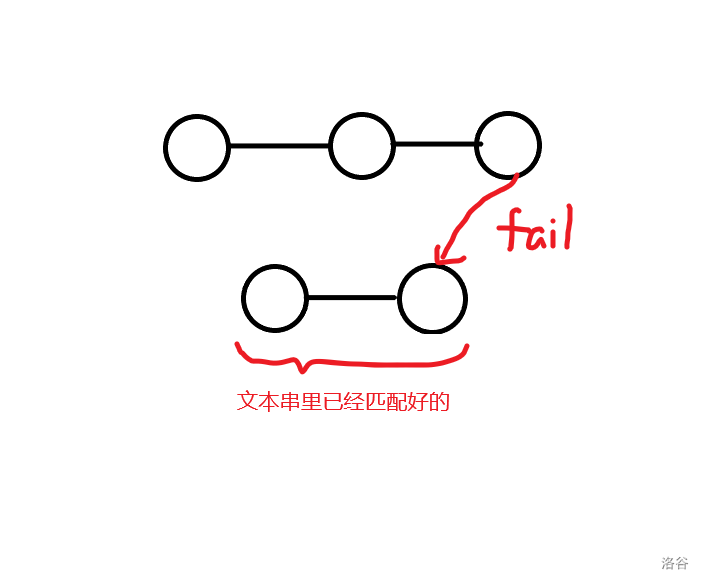
那么用\(fail\)打完标记后,对于每个模式串,就可以通过在\(TRIE\)上找标记点来得到最长的前缀了
void build()
{
for(int i = 1;i <= 4;i++) tr[0][i] = 1;
q.push(1);
fail[1] = 0;
while(!q.empty())
{
int u = q.front();
q.pop();
for(int i = 1;i <= 4;i++)
{
int v = tr[u][i];
if(!v)
{
tr[u][i] = tr[fail[u]][i];
continue;
}
fail[v] = tr[fail[u]][i];
q.push(v);
}
}//板子
int p = 1;
for(int i = 1;i <= lent;i++)
{
p = tr[p][getid(t[i])];
for(int k = p;k && !vis[k];k = fail[k]) vis[k] = 1;
}//用文本串跑trie,通过fail标记出现了的前缀
}
void getans()
{
for(int i = 1;i <= m;i++)
{
//每个文本串跑一边trie找最远的标记点
int res = 0;
int l = strlen(s[i] + 1);
int p = 1;
for(int j = 1;j <= l;j++)
{
p = tr[p][getid(s[i][j])];
if(vis[p]) res = j;//j单增,就这样写
}
printf("%d\n",res);
}
}
P2444 [POI2000] 病毒
输出TAK白拿60
有点莫名其妙
画了个大图才明白
一个病毒出现的充要条件就是当前点\(p\)跳到了某个串的尾巴上,那么如果不想让病毒出现,就需要找到一条长度无限的路径,该路径不经过所有病毒串的尾巴节点
长度无限,就是在环里兜圈子
所以就是看字典图上是否存在一个环,该环不经过所有病毒串的尾巴节点
以题干中的一组病毒为例
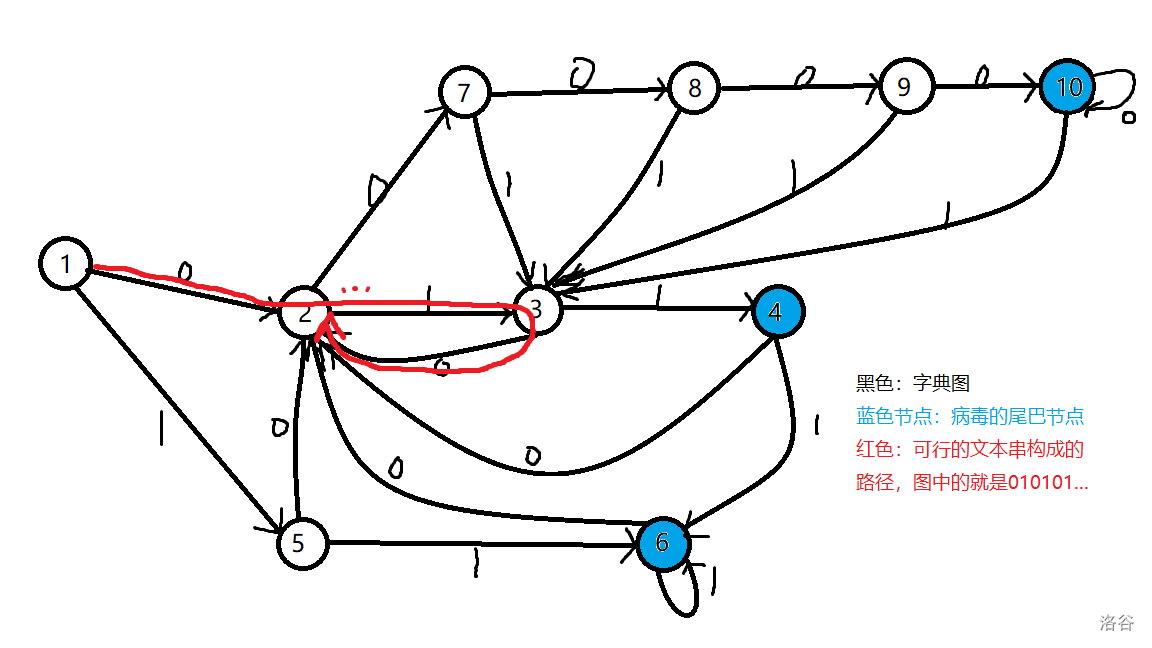
那么用搜索找符合条件的环即可
//超原始代码
//tr已经经过AC::build()了
void dfs(int x)
{
if(vis[x] == 1)
{
ans++;
return;
}
vis[x] = 1;
for(int i = 0;i <= 1;i++)
{
int u = tr[x][i];
if(vis[u] == 2) continue;
dfs(u);
vis[u] = 0;
}
}
//44pts
优化:另开一个数组记录当前点是否在搜索路径上,在搜索完毕时进行重置
void dfs(int x)
{
ifvis[x] = 1;//将当前点记为在路径上
for(int i = 0;i <= 1;i++)
{
int u = tr[x][i];
if(ifvis[u])//下一步就在该路径上
{
ans++;//有合法环
return;
}
if(!wei[u] && !vis[u])//
{
vis[u] = 1;
dfs(u);//继续沿该路径找
}
}
//此时出了循环,说明上一条路径搜完了,重置标记
ifvis[x] = 0;
}
怎么才\(76pts\)
这和上面的一张图有关

如果下面一行的后一个节点是尾巴节点呢?
说明上面一行的最后一个即使不是尾巴节点也不能走
所以要根据\(fail\)多打标记
if(!v)
{
tr[u][i] = tr[fail[u]][i];
if(vis[fail[u]] == 2) vis[u] = 2;//根据fail打标记
continue;
}
fail[v] = tr[fail[u]][i];
if(vis[fail[u]] == 2) vis[v] = 2;//根据fail打标记
q.push(v);
以此可见\(fail\)指针的一个重要含义:指向的是当前已匹配的最长后缀
奇美拉
P2322 [HNOI2006] 最短母串问题
\(dp\)+状压+字符串匹配
状压有点像Bill的挑战
现在就是要把这东西放到自动机上
众所周知匹配上一个串就是经过他的尾巴点,那么我们就在跳到尾巴时把对应编号位搞成\(1\)
S[u] = 1 << (id - 1);
这里再结合\(fail\)的含义,还要把\(fail\)两端节点的状态合并一下(不写\(80pts\))
S[u] |= S[fail[u]];
然后\(bfs\),每走到一个点就继承(按位或)一下他的状态,直到继承完所有模式串结束的状态
然后就得到超暴力\(50\)分代码
很显然,存储方式太\(low\)了
事实上,一般的\(dp\)问的是最小长度,那很明显,这题还要用记录路径的方法来搞答案
原先的代码就像\(dfs\)一样把信息都扔进了队列,浪费空间,所以采用新的方法
不妨记录每次的跳动是在第几次的跳动上进行的,所以设\(fa_i\)表示第\(i\)次跳动是在第\(fa_i\)次跳动进行的
分散的跳动都聚在循环内部,所以出了循环才相当于进行了一次大的跳动(换了一个分散点)
最后在根据路径还原串,然后倒序输出即可
这里还用到了\(bfs\)的优势:考虑到每一次循环都是按字典序来的,所以一旦找到了第一个答案,毫无疑问一定是最短且字典序最小,此时输出完后直接退出即可
void solve()
{
vis[1][0] = 1;//vis[u][s]表示节点u的状态为s的情况是否已经遍历
node tmp;
tmp.idx = 1,tmp.nowS = 0;
q1.push(tmp);
p = 0;//记录大的跳跃
while(!q1.empty())
{
node u = q1.front();
q1.pop();
if(u.nowS == ((1 << n) - 1))
{
while(p)
{
//printf("p:%d\n",p);
ans[++sum] = path[p];
p = fa[p];
}//回溯路径
for(int i = sum;i >= 1;i--) printf("%c",ans[i] + 'A');
return;//直接退出
}
for(int i = 0;i < 26;i++)//这里面所有的跳跃(push了的)都是在第p次跳跃的基础上进行的
{
int v = tr[u.idx][i];
if(!vis[v][u.nowS | S[v]])
{
vis[v][u.nowS | S[v]] = 1;//打标记
fa[++cnt] = p;//意义如上
path[cnt] = i;//记录该次跳跃对应的字符
node x;
x.idx = v,x.nowS = u.nowS | S[v];
q1.push(x);//push新节点
}
}
p++;//小跳完了是大跳
}
}
坑点:重复串(不写\(90pts\))
S[u] |= 1 << (id - 1);