by TheBigYellowDuck
记录一些网络流建模的实际例题吧。
相关链接:[[网络流 24 题]],[[Day 6 Part I]]
Part I. 二分图 & 最大流
- 满流:可以根据是否满流判断合法。
- 匹配:一些二分图的经典建模还是要记住的,往往用一条 \(S\to T\) 的路径表示一次匹配。
最小点覆盖 = 最大匹配 = 最大边独立集。最大点独立集 = 总点数 - 最大匹配 = 最小边覆盖。
一些构造方法:
- 最小点覆盖:取左部所有非匹配点,沿着”非匹配边 \(\rightarrow\) 匹配边 \(\rightarrow\) 非匹配边 \(\rightarrow \cdots\) ”走下去,经过的点打标记。这里是一个 DFS 过程,也就是要走过所有能走的路。所有未被打标记的左部点和打了标记的右部点构成最小点覆盖。
- 最大点独立集:最小点覆盖取补集。
- 最小边覆盖:选取所有匹配边,剩下没被覆盖的点任选一条出边。
- 最大边独立集:最大匹配。
Hall 定理:二分图存在完美匹配,当且仅当对于任意左部点的子集 \(S\),其邻域 \(T\) 满足 \(|S| \leq |T|\)。
P2891 [USACO07OPEN] Dining G
一个类似“三分图”的建模。
建立超级源汇,源点向食物连边,奶牛喜欢的食物向奶牛连边,奶牛向喜欢的饮料连边,饮料向汇点连边。容量都为 \(1\)。
为了限制奶牛只能匹配一次,考虑拆点,点限制转边限制即可。最大流就做完了。
时间复杂度 \(\mathcal{O}(n^3)\)。
P2857 [USACO06FEB] Steady Cow Assignment G
对于最小化极差问题,考虑二分答案 \(x\),暴力枚举最小名次 \(r\),那么最大名次就是 \(r+x-1\)。也就是要把每头牛都安排到它们第 \([r,r+x-1]\) 喜欢的牛棚里。
这就是个匹配问题。建立超级源汇,源点向牛连边,容量为 \(1\),牛向牛棚连边,容量为 \(1\),牛棚向汇点连边,容量为牛棚能容纳的上限。如果满流,说明所有牛都住进去了,即合法。
时间复杂度 \(\mathcal{O}(n\sqrt{n}\times B^2\log B)\)。
P3153 [CQOI2009] 跳舞
好题。
一个人对于喜欢和不喜欢的异性的限制是不一样的,只用一个点很难描述这件事情。于是考虑拆点,对每个人拆出来三个点,一个作为连源汇的虚点,虚点连出去两个点,一个用来连其喜欢的人,一个用来连其不喜欢的人。
和喜欢的人跳舞可以随便跳,所以虚点向表示喜欢的点连边容量为 \(+\infty\)。
怎么限制只能和不超过 \(k\) 个不喜欢的人跳舞?虚点向表示不喜欢的点连边容量为 \(k\) 即可。
怎么求匹配轮数的最大值?考虑二分答案 \(x\),源点向男生连容量为 \(x\) 的边,女生向汇点连容量为 \(x\) 的边。如果最后满流,就判定为合法。
时间复杂度 \(\mathcal{O}(n^4 \log n)\)。
P2055 [ZJOI2009] 假期的宿舍
题目说的好抽象。读了好长时间。
所有在校学生无论回不回家都会提供一个床位,那么把除了不回家的在校学生以外的人看作左部点,床看左右部点,每个人向自己能睡的床连边,就是一个二分图最大匹配。
有合法安排方案的充要条件是最大流等于左部点点数,也就是满流。
时间复杂度 \(\mathcal{O}(m\sqrt{n})\)。
P6268 [SHOI2002] 舞会
二分图最大独立集。用 总点数 - 最大匹配 即可。求最大匹配直接最大流。
时间复杂度 \(\mathcal{O}(m\sqrt{n})\)。
P2172 [国家集训队] 部落战争
每个点向其下一步能跳到的点连边,横坐标小的连向横坐标大的,会形成一张 DAG。要求的是这张 DAG 的最小路径覆盖。
这是网络流 24 题中的经典建模。按照 [[网络流 24 题#P2764 最小路径覆盖问题]] 的方法拆点处理即可。本质还是转成了一个二分图匹配问题。
时间复杂度 \(\mathcal{O}(n^3m^3)\)。
P4251 [SCOI2015] 小凸玩矩阵
二分答案 \(x\),由于需要最小化答案,要判定能否选出 \(n-k\) 个数 \(<x\)。
每行每列至多选一个,考虑经典二分图建模,把行号和列号作为左右部,对于每个 \(a_{i,j} < x\),让 \(i \rightarrow j\) 连边。最大匹配 \(\leq n-k\) 说明合法。
时间复杂度 \(\mathcal{O}(n\sqrt{n}\log V)\)。
P2825 [HEOI2016/TJOI2016] 游戏
如果没有硬石头,就是一个经典的模型。
现在有了一些硬性的分隔,其实本质没什么区别。对每行每列找出极长的被分割出来的子段,给它们重新标号,对于每个格子,在它行标号和列标号之间连边即可。
然后就是一个最大匹配。
时间复杂度 \(\mathcal{O}(nm\sqrt{n+m})\)。
UVA10330 Power Transmission
很典的建模套路手段。
多源多汇,就建立超级源汇,超级源向每个源点连容量为 \(+\infty\) 的边,每个汇点向超级汇连容量为 \(+\infty\) 的边。点有容量限制,那就拆点。
时间复杂度 \(\mathcal{O}(n^2m)\)。
UVA12125 March of the Penguins
类似 [[Day 6 Part I#P2472 SCOI2007 蜥蜴]] 的建模方法。
每个点拆成出入点,容量为能被跳出的次数。源点向每个点的入点连边,容量为初始的企鹅数量。能跳到的点之间互相连边,容量为 \(+\infty\)。
考虑枚举汇聚点。由于限制是跳出的次数,所以要以入点作为汇点。可以再建一个超级汇点,入点向超级汇连边,容量为 \(+\infty\)。
时间复杂度 \(\mathcal{O}(n^3)\)。
P5038 [SCOI2012] 奇怪的游戏
经典题。
相邻格之间的操作问题,考虑黑白染色。
令 \(S_B\) 表示黑格的和,\(S_W\) 表示白格的和,会发现一次操作不会改变 \(S_B-S_W\) 的值。
令黑格有 \(B\) 个,白格有 \(W\) 个,最终所有数都变为 \(X\)。利用黑格的和和白格的和可以分别算出来一个操作次数,显然应该相等。所以有
\[B\times X-S_B=W\times X-S_W \]在 \(B\neq W\),也即 \(n,m\) 均为奇数的情况下,我们可以直接得到唯一可能的 \(X\),还需要判断是否合法。而如果 \(B=W\),也即 \(n,m\) 有偶数的情况,我们就解不出来 \(X\) 了。
注意到,在 \(B=W\) 时,答案具有单调性。如果 \(X\) 合法,那么能够给所有格子 \(+1\) 使得 \(X+1\) 合法。考虑二分答案 \(X\),转化为判断 \(X\) 是否合法。
容易想到二分图多重匹配的建模方式。每个点必须被匹配 \(X-a_{i,j}\) 次,如果存在完美匹配就合法。
时间复杂度 \(\mathcal{O}(nm\sqrt{n+m}\log W)\)。
P4298 [CTSC2008] 祭祀
根据 Dilworth 定理,DAG 上最长反链长度,等于最小链覆盖数量。由于需要知道每个点对之间的偏序关系,需要先跑一遍传递闭包,在此基础上做最小链覆盖。
Subtask 1:构造一条最长反链。
方法:在最小链覆盖建立的二分图上找到一个最大独立集 \(I\),所有 \(i\) 满足 \(i_1,i_2 \in I\) 构成集合 \(A\),则 \(A\) 为最大反链。
证明:设最大匹配为 \(M\),则最小点覆盖大小为 \(|M|\),进而 \(|I|=2n-|M|\)。
考虑把 \(|I|-|A|\) 看作「\(i_1\not\in I\) 或 \(i_2\not\in I\)」的 \(i\) 构成的集合的大小,显然不超过 \(n\),从而 \(|I|-|A| \leq n\),进而有 \(|A|\geq |I|-n=n-|M|\)。
而 \(|A|\) 再大也不可能超过「左部点 - 最大匹配」这么大,也就是 \(|A| \leq n-|M|\),从而 \(|A|=n-|M|\)。
Subtask 2:判定每个点 \(i\) 能否作为最长反链。
方法:删掉 \(i\) 和所有与 \(i\) 有偏序关系的点,也就是钦定该点被选中,再计算最长反链,如果答案恰好减少了 \(1\),那么 \(i\) 就可以,否则不行。证明显然。
时间复杂度 \(\mathcal{O}(n^3\sqrt{n})\)。
P4311 士兵占领
首先把士兵分成两类,同时为行列做出贡献(贡献为 \(2\))的士兵,以及仅用来补齐行或列的限制的(贡献为 \(1\))的士兵。设两类士兵分别放了 \(c_2,c_1\) 个,可以得到关系式:
\[2c_2+c_1=\sum l_i+\sum c_i \]我们想让贡献为 \(2\) 的士兵尽量多,不难看出这是一个经典的二分图建模。把行号作为左部点,列号作为右部点,所有可以放士兵的格子 \((i,j)\) 连一条 \(i\to j\) 的容量为 \(1\) 的边。
源点连左部点,容量为 \(l_i\),右部点连汇点,容量为 \(c_i\)。这个图的最大匹配就是最多的 \(2\) 士兵数。
时间复杂度 \(\mathcal{O}(nm\sqrt{n+m})\)。
UVA10779 Collectors Problem
好题!
每个朋友只会换出自己多余的牌,换进来自己没有的牌。从牌的角度来考虑,每个不同种类的牌最多从 Bob 手里换到朋友手里一次,朋友最多把自己重复了 \(k\) 次的牌换给 Bob \((k-1)\) 次。
考虑用流来描述这个过程。对于每种牌建一个点 \(a_i\),源点向 \(a_i\) 连边的容量为 Bob 初始时拥有 \(i\) 的数量,\(a_i\) 向汇点连边,容量为 \(1\) 表示不同种类数。
对每个朋友建一个点 \(b_i\),对于所有朋友 \(i\) 没有的牌 \(j\),连边 \(a_j\to b_i\),容量为 \(1\) 表示换进来至多一次。对于朋友 \(i\) 有的牌 \(j\),设他有 \(k\) 张,连边 \(b_i \to a_j\),容量为 \(k-1\) 表示至多换出去 \(k-1\) 次。
对于一条流 \(S\to T\),先是 \(S \to a\) 出发,表示 Bob 一开始有,后面经历若干次 \(b \to a\) 表示交换,最后从 \(a \to T\) 计入答案。
时间复杂度 \(\mathcal{O}((n+m)^2nm)\)。
UVA1306 The K-League
双倍经验 P1264。
考虑如何判断 \(i\) 是否能获胜,自然钦定 \(i\) 剩下未确定的比赛全胜,只需要保证其他人的胜场不大于 \(i\)。设 \(i\) 在剩余场次全胜得到的胜场为 \(X\)。
考虑经典的边对点建模,把比赛作为左部点,队伍作为右部点,每场比赛向其双方连边,容量为 \(+\infty\)。源点向比赛连边,容量为 \(a_{ij}\) 表示需要比的场次。每个队伍向汇点连边,容量为 \(X-w_i\) 表示其他人最多只能胜这么多场。如果最大流等于需要比的场次,说明存在一种合理的安排,\(i\) 就可以获胜。
时间复杂度 \(\mathcal{O}(n^4)\)。
Part II. 最小割
- 割集大小:用一些数值转换的 trick。比如「收入 - 成本」可以考虑用总和减去某种最小割。
- 二者选其一:与源汇相连分别代表处于不同集合,割掉某一边要付出相应的代价。
- 最大权闭合图:源点连正权点,负权点连汇点,用正权值和减去最小割。
最小割的必须边与可行边:
- 可行边:满流,且残量网络上不存在 \(u\) 到 \(v\) 的路径。
- 必须边:满流,且残量网络上源点与 \(u\) 连通,\(v\) 与汇点连通。
P1344 [USACO4.4] 追查坏牛奶 Pollutant Control
能看出来,就是要求一个 \(1,n\) 的割集。第一问就是裸的最小割。
第二问有一个 trick。我们把边权 \(w\) 变成 \(kw+1\),其中 \(k\) 是一个足够大的常数。这样得到最小割 \(f'\),实际上的最小割就是 \(\lfloor f'/k\rfloor\),割集大小就是 \(f' \bmod k\)。
另一种做法是,先求出最小割,把满流的边容量设为 \(1\),其他边容量设为 \(+\infty\),再跑一遍最小割即可。
时间复杂度 \(\mathcal{O}(n^2m)\)。
P1345 [USACO5.4] 奶牛的电信 Telecowmunication
割是边集,而这道题让我们做点上的最小割。
那我们拆点就好了。每个点拆成两个点,之间连上容量为 \(1\) 的边表示割掉的代价。原图中的边容量设为 \(+\infty\) 表示不可割。这样的最小割就是答案。
时间复杂度 \(\mathcal{O}(n^2m)\)。
P2944 [USACO09MAR] Earthquake Damage 2 G
与上一道题差不多的思路。拆点,做最小割。
把 \(1\) 的出点 \(1_{\text{out}}\) 当作超级源点,新建超级汇点。所有不能割的点向汇点连容量为 \(+\infty\) 的边。
时间复杂度 \(\mathcal{O}(n^2m)\)。
P5030 长脖子鹿放置
会发现一个棋子只能跳到与其行号奇偶性不同的格子上。考虑按照行号的奇偶性分组,建立二分图,互斥的格子之间连边。
建立超级源汇,分别连接左右部点,容量为 \(1\) 表示割掉的代价。二分图内部的边容量为 \(+\infty\) 以保证不会被割掉。把割掉的边理解为不选即可。
最小割。答案为 \(nm-k-|f|\)。
认为 \(n,m\) 同阶。时间复杂度 \(\mathcal{O}(n^3)\)。
P1361 小 M 的作物
好题。
先不考虑点集的贡献,那就是一个很经典的“二者选其一”的问题。每个点向源点和汇点连边,表示位于该集合的收益,最小割就是放弃的收益,用总和减一下即可。
现在有了点集的贡献,会发现其贡献分为三种,连 \(A,B\) 或者没有。这就不是一个二选一了。
对于一个点集 \(S\),只有当 \(S\) 中所有点都割了到源点的边才会得到连向汇点的额外收益,反过来也是一样。而如果 \(S\) 中同时存在割了源点和割了汇点的点,那么两边的收益都要放弃。也就是说,这个收益应该是和怎么割”并联“在一起的。
考虑这么建图:
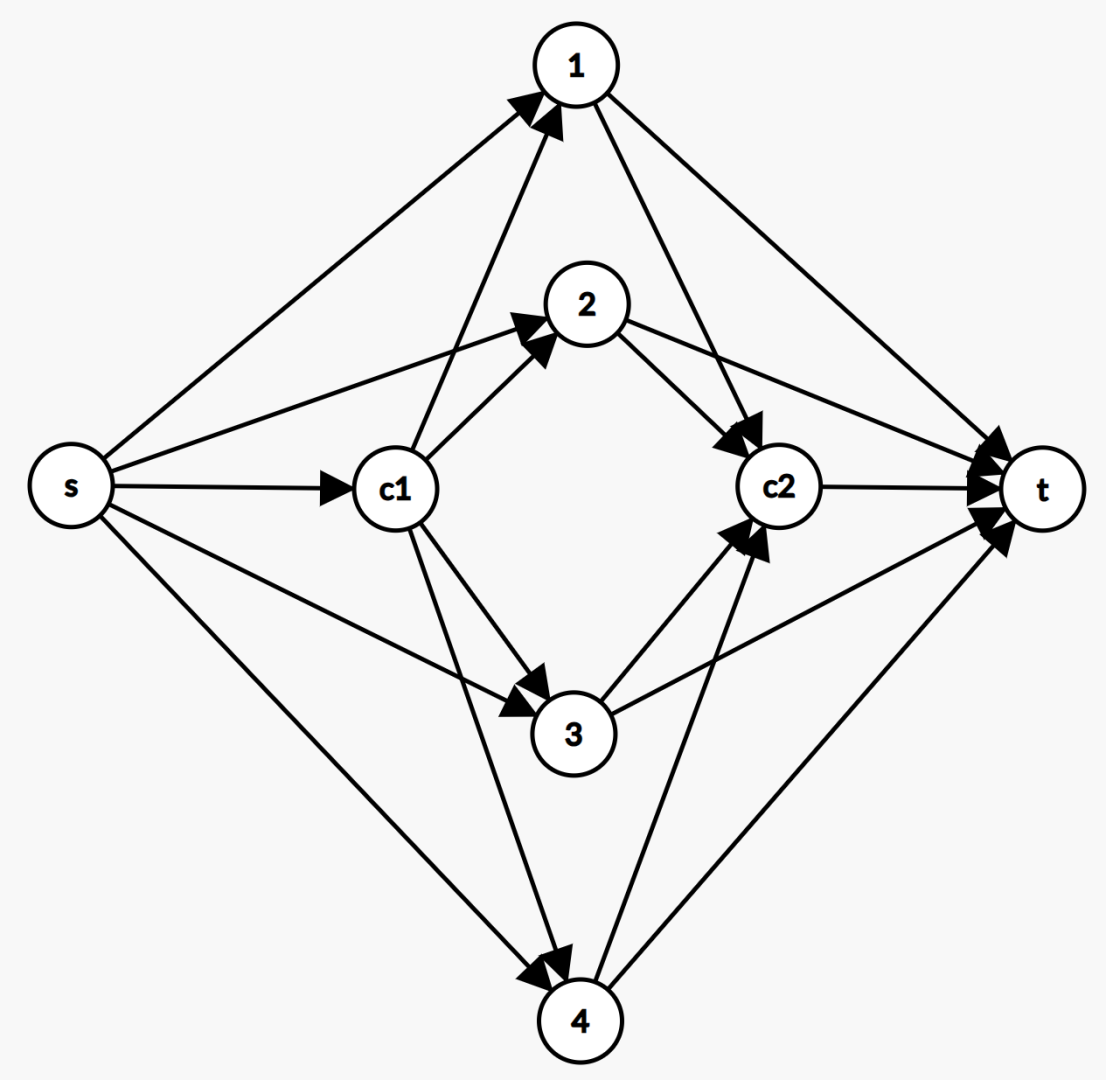
\(c_1,c_2\) 与源汇相连的容量为点集的收益,与点集内的点相连的容量为 \(+\infty\) 表示不会被割。
会发现这张图里的最小割能够算入额外收益。因为如果点集内割不同边,那么 \(c_1,c_2\) 必然都要被割才会使得 \(s,t\) 不连通。最小割即可。
时间复杂度 \(\mathcal{O}\left((n+m)^3\right)\)。远远跑不到上限。
fun fact:这道题把我的 Dinic 卡了。然后发现自己写了个假的 Dinic。
P2598 [ZJOI2009] 狼和羊的故事
把狼和羊分到两个集合中去,也就是要在原本的冲突中选择一些断掉,容易想到最小割。
建立源汇,源点向狼连边,羊向汇点连边,容量为 \(+\infty\) 表示不能割。每个格子向四周连边,容量为 \(1\),表示建立篱笆的代价。最小割即可。
认为 \(n,m\) 同阶,时间复杂度 \(\mathcal{O}(n^3)\)。
P3308 [SDOI2014] LIS
与网络流 24 题中某个题类似的建模。
先跑一遍 dp,得到 \(f(i)\) 表示以 \(i\) 为结尾的 LIS 长度。因为我们要割掉的是点,所以先拆点,把容量放到出入点之间的连边上,表示割掉的代价。
设最终得到的 LIS 长度为 \(L\),源点向所有 \(f(i)=1\) 的点连边,所有 \(f(i)=L\) 的点向汇点连边。对于每个转移式 \(f(j)=f(i)+1\),让 \(i\) 向 \(j\) 连边。容量都是 \(+\infty\) 表示不割。
这张图上所有的路径都是一条合法的 LIS。因为我们要使得 LIS 长度减小,所以要求源汇不连通。那么最小割就是第一问的答案。
接下来还需要最小化附加权值的字典序。感觉到,这个东西应该要在最小割的可行边上入手。
把所有边按照 \(c_i\) 排序,依次判断是否为可行边。BFS 判断残量网络上能不能走通即可。如果钦定了这条边为割边,需要从入点向源点,汇点向出点退流,直至找到所有割边。
时间复杂度 \(\mathcal{O}(n^5)\)。实际上哪里都跑不满·。
SP839 OPTM - Optimal Marks
二进制下每位独立,逐位考虑,转化为只有 \(0/1\) 的问题。自然想到“二者选其一”的最小割模型。
建立源汇,与源点相连表示为 \(1\),与汇点相连表示为 \(0\)。已经确定标号的点先连上。原图中的边连双向,表示割掉的代价。最小割即可。
构造每个点的权值,可以从源点出发 DFS,搜到的点这一位上都为 \(1\)。
时间复杂度 \(\mathcal{O}(n^2m \log V)\)。
P3410 拍照
最大权闭合子图。
要求拍照的人会对答案做出正贡献,下属会给答案做出负贡献。选正贡献的人必须带着下属一起选。
正权点连源点,负权点连汇点,容量为权值的绝对值。内部的边容量为 \(+\infty\)。
与源点割掉的正权点理解为不要,与汇点割掉的负权点理解为要。用正权之和减去最小割即为答案。
时间复杂度 \(\mathcal{O}(m\sqrt{n})\)。
P2805 [NOI2009] 植物大战僵尸
只能从右往左进攻,且如果想要吃掉一棵植物,必须要把所有保护它的植物都吃掉。
每棵植物向其依赖的植物连边,会发现这就是一个最大权闭合子图的问题。
然而这个是有问题的。如果植物依赖关系成环,那就一个也吃不掉了。我们先建反向边,拓扑排序去掉所有环,在剩下的图中做最大权闭合子图即可。
时间复杂度 \(\mathcal{O}(n^3m^3)\)。
UVA1389 Hard Life
最大密度子图。
这个问题是要我们选出一个子图 \(G'=(V',E')\),满足 \(D=\dfrac{|E'|}{|V'|}\) 最大。
令 \(n=|V|\),\(m=|E|\)。
要求的是一个分数的最大值,想到 01 分数规划。
把 \(D\) 形式化地写出。
\[D=\dfrac{\sum_{e\in E} x_e}{\sum_{v\in V}x_v} \]这里的 \(x\in \{0,1\}\) 表示选没选。对于选了的一条边,要求其两个端点也必须选。
二分答案 \(g\),令
\[h(g)=\max\left\{\sum_{e\in E}1\times x_e-\sum_{v\in V}g\times x_v\right\} \]当 \(D\) 取得最大值时,\(h(g)=0\)。可以发现,\(h(g)\) 随着 \(g\) 单调递减。
考虑二分答案的上下界和精度。取下界为 \(\dfrac{1}{n}\),上界为 \(m\)。
对于两个子图 \((V_1,E_1)\) 和 \((V_2,E_2)\),密度相减得到
\[\dfrac{m_1}{n_1}-\dfrac{m_2}{n_2}=\dfrac{m_1n_2-m_2n_1}{n_1n_2}\geq \dfrac{1}{n_1n_2}\geq \dfrac{1}{n^2} \]当上界与下界之差小于 \(\dfrac{1}{n^2}\) 时,就已经确定找到了答案。所以精度设置为 \(\dfrac{1}{n^2}\)。
现在考虑怎么计算 \(h(g)\)。
算法 1:把图上的边和点都看成点,边的点权为 \(1\),点的点权为 \(-g\)。对于原图中的边,从边代表的点向其两个端点连边。这张图的最大权闭合图就是 \(h(g)\)。
最大权闭合图的权值不会小于 \(0\),只需要找使得 \(h(g)=0\) 的最小的 \(g\)。
时间复杂度 \(\mathcal{O}((n+m)^2m\log n)\)。
算法 2:我们继续挖掘一些性质。发现,导出子图一定是最优的。
那么,对于导出子图 \(G'=(V',E')\),可以把 \(E \setminus E'\) 看成是 \(V'\) 与 \(V \setminus V'\) 的割集。
由于 \(h(g)=|E'|-g|V'|\),最大化 \(h(g)\) 相当于最小化 \(g|V'|-|E'|\)。
令 \(\text{deg}(u)\) 为点 \(u\) 的度数,则有
\[\begin{aligned} g|V'|-|E'|&=\sum_{v\in V'}g-\sum_{e \in E'}1 \\ &=\sum_{v\in V'}g-\dfrac{1}{2}\left(\sum_{v\in V'}\text{deg}(v)-c(V',V\setminus V')\right) \\ &= \dfrac{1}{2} \left(c(V',V \setminus V')+\sum_{v\in V'}2g-\text{deg}(v)\right) \end{aligned} \\ \]这里的 \(c(S,T)\) 表示点集 \(S,T\) 的割。
把后半部分算入最小割,可以让每个点 \(v\) 向汇点连一条容量为 \(2g-\text{deg}(v)\) 的边。因为容量不能是负数,所以需要加上一个偏移量 \(U\)。因为度数不超过 \(m\) 且 \(g\) 非负,所以 \(U\) 取 \(m\) 就可以。
整体建图结构:
- 原图中 \((u,v)\) 替换为两条有向边,容量为 \(1\)。
- 源点与每个点相连,容量为 \(U\)。
- 每个点与汇点相连,容量为 \(U+2g-\text{deg}(v)\)。
跑出来的最小割 \(c(S,T)\) 并不直接是 \(h(g)\)。进一步转化有
\[h(g)=\dfrac{U \times n-c(S,T)}{2} \]时间复杂度 \(\mathcal{O}(n^2m\log n)\)。
注意:inf 不要设置太大。在 double 下会出奇怪问题。
UVA1515 水塘 Pool construction
容易看出“二者选其一”的模型。
建立超级源汇,每个点与源点相连表示作为草地,与汇点相连表示作为水洼。
边界上的点都要作为草地,那么每个点向源点连边容量为 \(+\infty\) 表示不可割。如果本来就是草地,那么向汇点连边容量为 \(0\) 表示不需要代价,否则容量为 \(f\)。
对于其他的点,如果其一开始是水洼,则与汇点连边容量为 \(f\),与源点连边容量为 \(0\)。反之同理。
对于相邻的点,互相连容量为 \(b\) 的边,如果处于不同集合,要把这条边割掉,表示建造围墙。
最小割即可。\(\mathcal{O}(n^3m^3)\)。
P1646 [国家集训队] happiness
非常经典的集合相关的最小割建模。
建立超级源汇,每个人与源点相连表示文科,与汇点相连表示理科。
考虑怎么处理两人同时选某科带来的贡献。只要对每一对关系建两个虚点,一个与源点相连表示共同选文科的贡献,一个与汇点相连表示共同选理科的贡献。
虚点向这一对的两个人连容量为 \(+\infty\) 的边表示不可割。这样如果两人位于不同集合,必须要同时割掉连向两边的虚点才能使源汇不连通,也就去掉了全部的贡献。
这样,最大的价值就是总和减去最小割。
时间复杂度 \(\mathcal{O}(n^3m^3)\)。
P1935 [国家集训队] 圈地计划
容易发现仍然是“二者选其一”的建模,然而这里一个点与周围的点位于不同集合会带来贡献。直接做不太行得通,需要想办法转成位于同一集合带来贡献。
这里有一个很巧妙的做法。对格子黑白染色,会发现每个格子的邻域都是异色格,那么我们可以交换每个黑色格子的 \(A,B\) 权值,这样就转成了位于同一集合带来 \(C\) 的贡献。
再按照经典建模手段跑最小割即可。\(\mathcal{O}(n^3m^3)\)。
P5295 [北京省选集训 2019] 图的难题
这个东西可以转化成任意子图 \(G'=(V',E')\) 都满足 \(|E'|\leq 2|V'|-2\)。否则,在这个子图当中没有不存在环的染色方案,那就挂了。
这样就可以得到 \(\max\{|E'|-2|V'|\} \leq -2\)。
这种问题的经典做法是把边和点都建成图上的点,边的点权为 \(1\),点的点权为 \(-2\)。每条边向其两个端点连边,求最大权闭合子图即可。
但是这里有一个问题,就是子图必须非空。所以我们依次钦定每个点必须被选,把这个点删了,求剩下点的最大权闭合子图。
时间复杂度 \(\mathcal{O}(Tnm\sqrt{n+m})\)。可以用退流等手段去掉根号。
[ARC085E] MUL
每个 \(x\) 向它的倍数连边。最大化没选择的,就是最小化选择的,就是最小权闭合子图。
权值取反,跑最大权闭合子图即可。
时间复杂度 \(\mathcal{O}(n^3 \log n)\)。
P4174 [NOI2006] 最大获利
感觉是一个很直白的建模。
对中转站和用户群建立点,源点连中转站,容量为 \(p_i\),用户群连汇点,容量为 \(c_i\)。每个用户群向 \(a_i,b_i\) 连容量为 \(+\infty\) 的边表示不可割。与源点相连表示不要,与汇点相连表示要。最后用所有用户群的总收益减去最小割,得到的就是「收益 - 成本」的值。
时间复杂度 \(\mathcal{O}((n+m)\sqrt{n+m})\)。
(todo)P3749 [六省联考 2017] 寿司餐厅
Part III. 最小割树
最小割树通常用来解决全局最小割问题。感觉只是一类科技,特征还算明显。
当我们需要跑很多次两点间最小割的时候,复杂度难以接受,就可以通过建最小割树来快速查询任意两点的最小割。因为最后转成树上路径问题,所以只能处理无向图的问题。
P4897 【模板】最小割树(Gomory-Hu Tree)
模板题。讲一下最小割树怎么建。
分治,对于一个集合中的点,任选两个 \(x,y\) 作为源汇求最小割,并将整个集合划分为与 \(x\) 相连的和与 \(y\) 相连的两部分。最小割作为 \((x,y)\) 的边权,对两个集合递归下去求解,直到集合大小为 \(1\)。
这样一共需要跑 \(n-1\) 次最小割,得到一个树型结构。在这棵树上,原图中任意两点的最小割就是树上路径的边权最小值,可以 \(\mathcal{O}(\log n)\) 查询。
时间复杂度 \(\mathcal{O}(n^3m+q\log n)\)。
UVA11594 All Pairs Maximum Flow
任意两点间最大流,枚举源汇暴力 Dinic 时间复杂度达到了惊人的 \(n^6\)。
使用最小割树,只需要跑 \(n\) 次最大流,两点之间的最大流可以 \(\log n\) 的树上倍增轻松解决。
时间复杂度 \(\mathcal{O}(n^5)\)。
P3329 [ZJOI2011] 最小割
建出最小割树,暴力枚举点对算树上边权最小值即可。
时间复杂度 \(\mathcal{O}(n^3m +q n^2)\)。后面这一部分的复杂度很容易优化,但是瓶颈不在这里,所以没必要。
P4123 [CQOI2016] 不同的最小割
建出最小割树,暴力枚举点对,树上倍增算路径最小值,去重一下即可。
时间复杂度 \(\mathcal{O}(n^3m)\)。
P4214 [CERC2015] Juice Junctions
一眼 All Pair Maximum Flow,最小割树直接上。
时间复杂度 \(\mathcal{O}(n^3m)\),看起来过不了,实际上由于 Dinic 的玄学复杂度可以很快爆过去。
这就是我们 Dinic 的力量!!!
CF343E Pumping Stations
首先还是建最小割树。但是接下来没有前面几个题那么一眼了。
考察全局边权最小值,由于两点之间的贡献为路径上边权最小值,贪心地考虑,不难说明这条边只会被经过一次。也就是说,断掉这条边后,我们会先在某棵子树中走完,通过这条边跳到另一棵子树里。
可以发现这是一个分治的结构,由此可以得到答案为最小割树上边权之和。构造方案也可以从分治的角度去考虑,当某个连通块只剩下一个点的时候就加上这个点,把两棵子树得到的路径拼起来即可。
时间复杂度 \(\mathcal{O}(n^3m)\)。
Part IV. 费用流
有些建模中,只有最大流难以表示全部的信息,就可以考虑费用流。
很多题目有两个维度的要求,比如价值和容量同时存在。
P2045 方格取数加强版
可以走 \(k\) 遍,但是只有第一次经过某个格子时才算贡献。
考虑用流量表示走的次数,费用表示得到的价值。需要一个最大费用最大流的建模。
先拆点,\(v \rightarrow (v_{\text{in}}, v_{\text{out}})\),把点权换成出入点之间的容量。出入点之间连两条边,一条容量为 \(1\) 费用为 \(a_{i,j}\),表示走一次得到的价值。另一条容量为 \(+\infty\) 费用为 \(0\),表示可以走任意多次,但是没有额外收益。
源点向 \((1,1)\) 连边,\((n,n)\) 向汇点连边,容量为 \(k\) 费用为 \(0\),表示最多走 \(k\) 次。
每个点向其右边和下边的点连边,容量为 \(+\infty\) 费用为 \(0\),表示可以走任意多次。
时间复杂度 \(\mathcal{O}(n^3)\)。
P2053 [SCOI2007] 修车
好题。
直接建模好像很困难,因为答案和技术人员修理的顺序有关,我们要在建模上体现这一点。
不妨直接计算每个人等待时间之和,最后除以 \(n\) 得到平均时间。
设技术人员 \(i\) 依次修理了车 \(j_1,j_2,\cdots,j_k\),那么会产生的贡献是 \(k\times T_{i,j_1}+(k-1)\times T_{i,j_2} +\cdots +T_{i,j_k}\)。这么拆一下会发现,贡献只与车被第几个修理有关。这启发我们进行拆点。
把每个技术人员拆成 \(m\) 个点,分别表示“正在修理倒数第 \(j\) 辆车的他”。每个点 \((i,j)\) 向车 \(k\) 连边,容量为 \(1\) 费用为 \(j\times T_{i,k}\)。源点和汇点分别连表示技术人员的 \(m \times n\) 个点和表示车的 \(m\) 个点,容量为 \(1\) 费用为 \(0\)。
最小费用最大流即可。
时间复杂度 \(\mathcal{O}(n^2m^3|f|)\)。
(todo)P2050 [NOI2012] 美食节
上一题的数据加强版。
P2153 [SDOI2009] 晨跑
这个有两问的答案看着很像最小费用最大流,启发我们把天数当作流,路程当作费用。
天数就是从 \(1 \sim n\) 不相交的路径数量。拆点,限制每个点只能经过一次。原图中的边权当成费用。源点就是 \(1_{\text{out}}\),汇点就是 \(n_{\text{in}}\),最小费用最大流即可。
时间复杂度 \(\mathcal{O}(nm|f|)\)。
P2517 [HAOI2010] 订货
最小成本,且单位货物有费用,考虑费用流建模,货物作为流量,价格作为费用。
对每个月建一个点,并建立超级源汇。源点提供货物,向每个月连边,容量为 \(+\infty\) 费用为 \(d_i\)。每个月向下一个月连边,容量为 \(S\) 费用为 \(m\)。每个月连向汇点,容量为 \(U_i\) 费用为 \(0\)。
要求月初库存与月底库存都为 \(0\),就是要求满流。由于源点能提供无限的流量,所以一定可以满流。最小费用最大流即可。
时间复杂度 \(\mathcal{O}(n^2|f|)\)。
P2604 [ZJOI2010] 网络扩容
第一问就是一个最大流。不需要费用的参与。
第二问可以在原来的残量网络上给每条边都加一条边,容量为 \(+\infty\) 费用为 \(w\),从源点流入 \(k\) 的流量,最小费用最大流就可以了。
原来的残量网络经过第一问后已经没有增广路了,这样新增的流量 \(k\) 一定都会通过新增的有费用的边流,从而保证了计算费用的正确性。
时间复杂度 \(\mathcal{O}(nm|f|)\)。
UVA1411 Ants
有个结论:任何两条线段不相交等价于所有线段长度之和最短。容易通过调整法证明。
类似想法在 2023 春测中也出现过。
将黑白点作为左右部,任意两点之间边权为距离。二分图最小权完美匹配,最小费用最大流即可。
时间复杂度 \(\mathcal{O}(n^3|f|)\)。
P4249 [WC2007] 剪刀石头布
双倍经验 CF1264E。
题目可以抽象为,对于 \(n\) 个点的竞赛图,其中一些边已经定向,给剩下的边定向,最大化三元环数量。
这个三元环看着很难办,正难则反,自然考虑最小化不形成三元环的三元组。可以发现在这样的三元组中必然存在一个点的出度为 \(2\),同时可以说明这是不形成三元环的充要条件。
设 \(u\) 的出度为 \(d_u\),那么 \(u\) 会形成 \(\frac{d_u(d_u-1)}{2}\) 个三元组。由于一个三元组内只能有一个点出度为 \(2\),这样统计同时是不重不漏的。这样我们只需要最小化 \(\sum_u \frac{d_u(d_u-1)}{2}\) 即可。
考虑一条边的贡献,它要么让 \(d_u \leftarrow d_u+1\),要么让 \(d_v \leftarrow d_v+1\)。我们把所有未确定的边当成左部点,每个点当成右部点,每条边向其两个端点连容量为 \(1\) 的边,这样就能够表示「增加出度」的意义。
现在的问题在于算贡献,因为我们的贡献是二次的。考虑对贡献差分,每个表示点的点向汇点连容量为 \(1\) 费用为 \(0,1,2,\cdots\) 的边,如果流满了 \([0,i]\) 的边,就表示贡献为 \(0+1+\cdots+i\)。这样连边是符合费用流的贪心性质的,也就是任意时刻流满的边都会是一个前缀。
最小费用最大流,答案为 \(\dfrac{n(n-1)(n-2)}{6}-\text{mincost}\)。构造方案只需要判断边的流量流到了哪个点上。
时间复杂度 \(\mathcal{O}(n^4)\)。
P4209 学习小组
最大化学生的同时最小化支出,考虑费用流建模。
源点连学生,容量为 \(k\) 费用为 \(0\)。每个学生连自己想去的小组 ,容量为 \(1\) 费用为 \(-f_j\)。注意到学生不需要选满 \(k\) 个小组,所以学生再连汇点,容量为 \(k-1\) 费用为 \(0\)。
每个小组连汇点。流的费用是二次的,于是差分掉,连容量为 \(1\) 费用为 \(c_i \times (2k+1)\) 的边。小组向汇点都会流一个前缀的边,\(1+3+5+\cdots (2k-1)=k^2\) ,自然就能得到平方的费用。
最小费用最大流,时间复杂度 \(\mathcal{O}(n^2m|f|)\)。
标签:连边,容量,复杂度,源点,建模,网络,最小,mathcal From: https://www.cnblogs.com/duckqwq/p/18132072