邻接表

感觉写的很好啊！
转载自：数组模拟邻接表 - AcWing

首先假设我们有n个点(n <= N)，m条边(m <= M)。

我们可以想一下对于任意一个结点u, 需要记录邻边的哪些信息。
这些信息应该包括这条邻边的终点，权重，以及下一条邻边的编号。
注意这里不需要记录邻边的起点，因为我们使用的时候都是给出起点的。
所以我们可以定义一个struct来表示邻边:

struct Edge
{
    int eid;    // 该条边的编号
    int e;      // 该条边的终点
    int w;      // 该条边的权重
    int nxt;    // 下一条邻边的编号
};

如果我们用上面的数据结构来记录邻边的信息，那么我们只需要定义如下变量来表示邻接表：

// 注意N和M的区别
int h[N];
Edge edges[M];
int eidx;

由于每条边都记录了下一条边的编号，这样我们只要把每个结点的第一条邻边的编号记录在h数组，我们就可以遍历它的每一条邻边了。

如果我们把Edge里的信息分开存到不同数组里，那么我们可以得到平时我们看到的变量定义：

// 注意N和M的区别
int h[N];
int e[M], w[M], nxt[M];  // 这三个数组等价于之前的Edge edges[M]，注意这些数组的下标表示邻边的编号
int eidx;

这里每个数组的下标的含义不一样。
关键的事情说三遍：h数组的下标为结点的编号，e,w,nxt数组的下标为边的编号，eidx为边的编号
关键的事情说三遍：h数组的下标为结点的编号，e,w,nxt数组的下标为边的编号，eidx为边的编号
关键的事情说三遍：h数组的下标为结点的编号，e,w,nxt数组的下标为边的编号，eidx为边的编号

如果理解了以上，下面就很好理解了。
有向图的邻接表存储就是对于每个点 u 对应一个头节点h[u]，记录第一条邻边的编号。
e, w, nxt数组的编号和建图的顺序有关，对于某一个点u, 它的所有邻边的编号不一定是连续的。
nxt[eidx]=h[u]; h[u]=eidx; 这个操作就是把新建的边插入表头。(先把新建的边的next指向现在队头的next，然后更新队头的next）
然后再eidx++, 给下一次建边使用

下边用图模拟一下加入四条边的过程

1. 初始状态

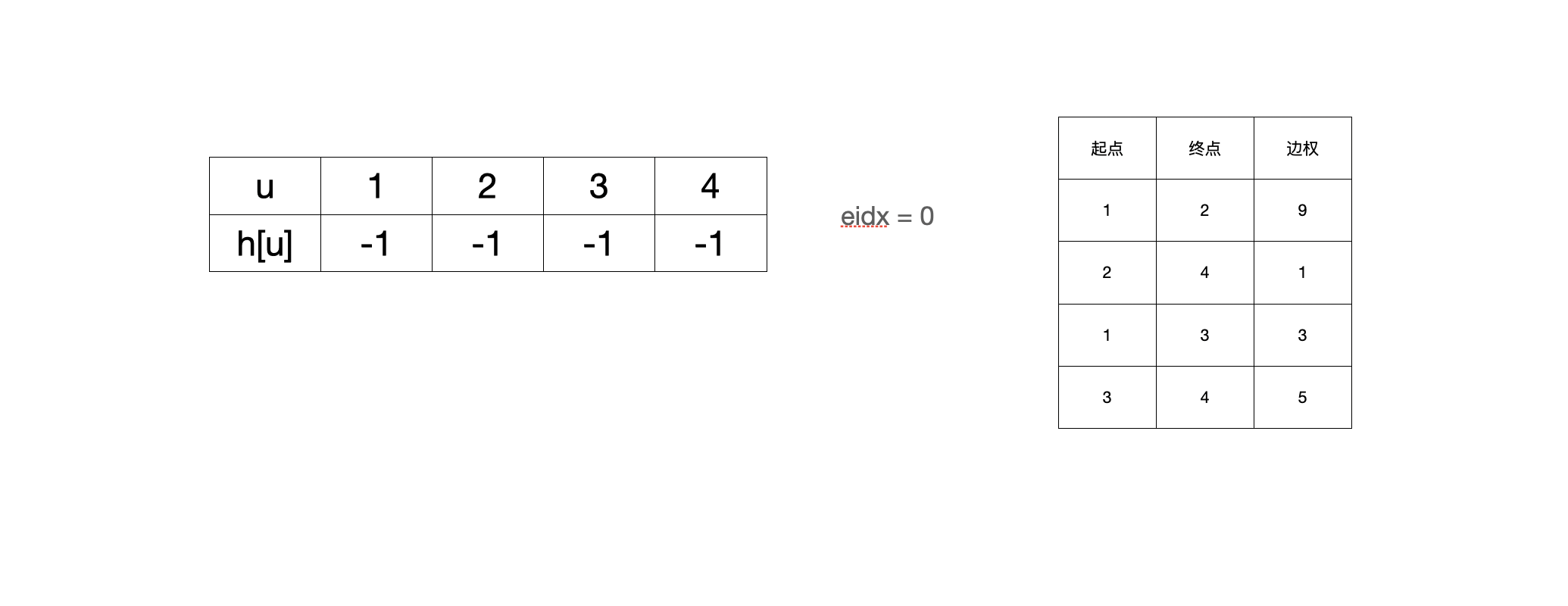
2. 加完第一条边(1,2,9)之后

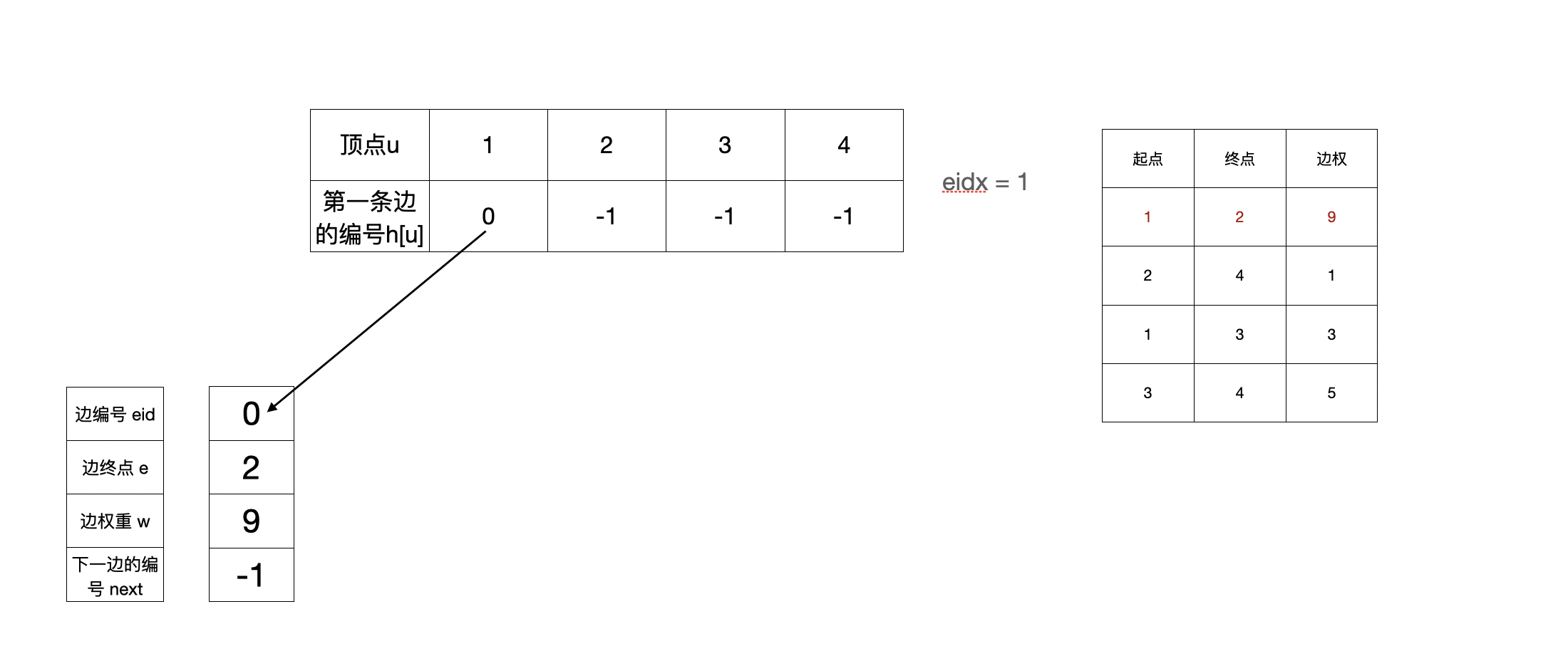
3. 加完第二条边(2,4,1)之后

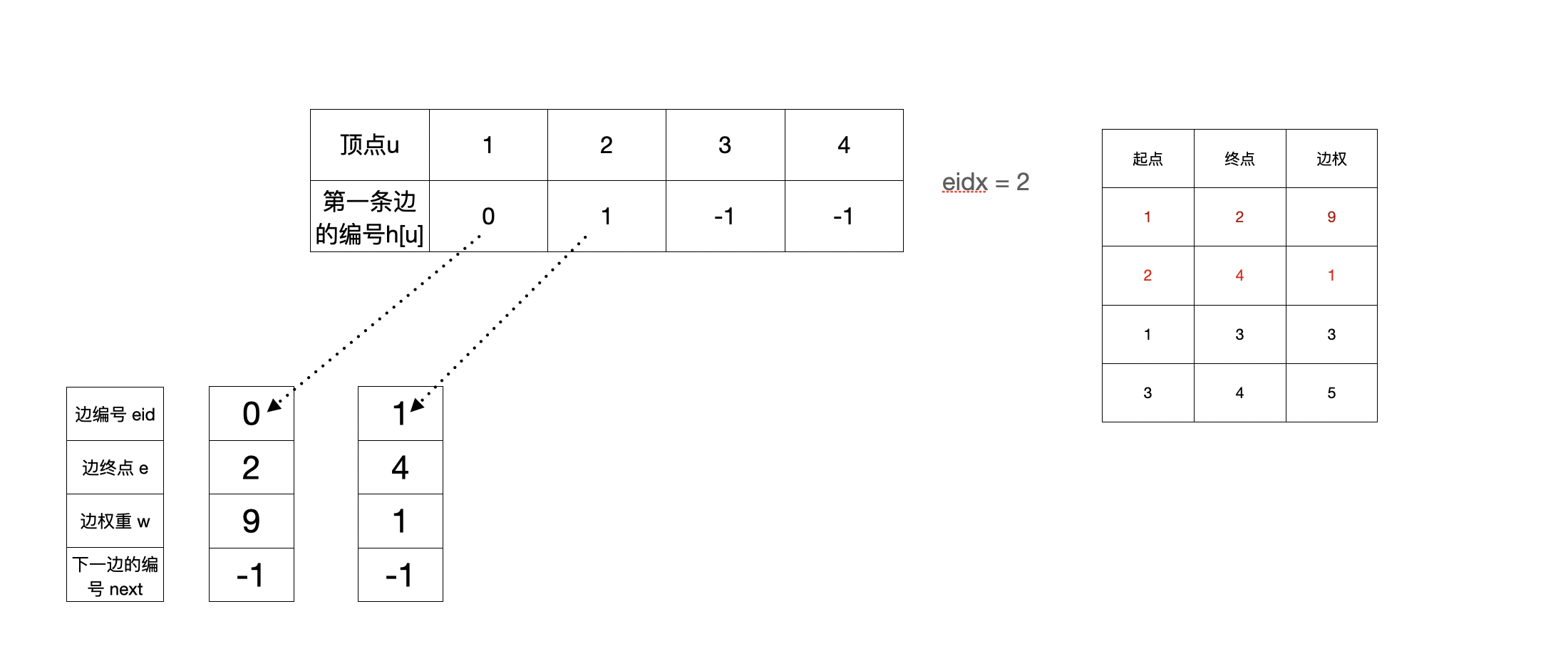
4. 加完第三条边(1,3,3)之后
   这里可以看到后加入的边，反而在邻接表的最前面

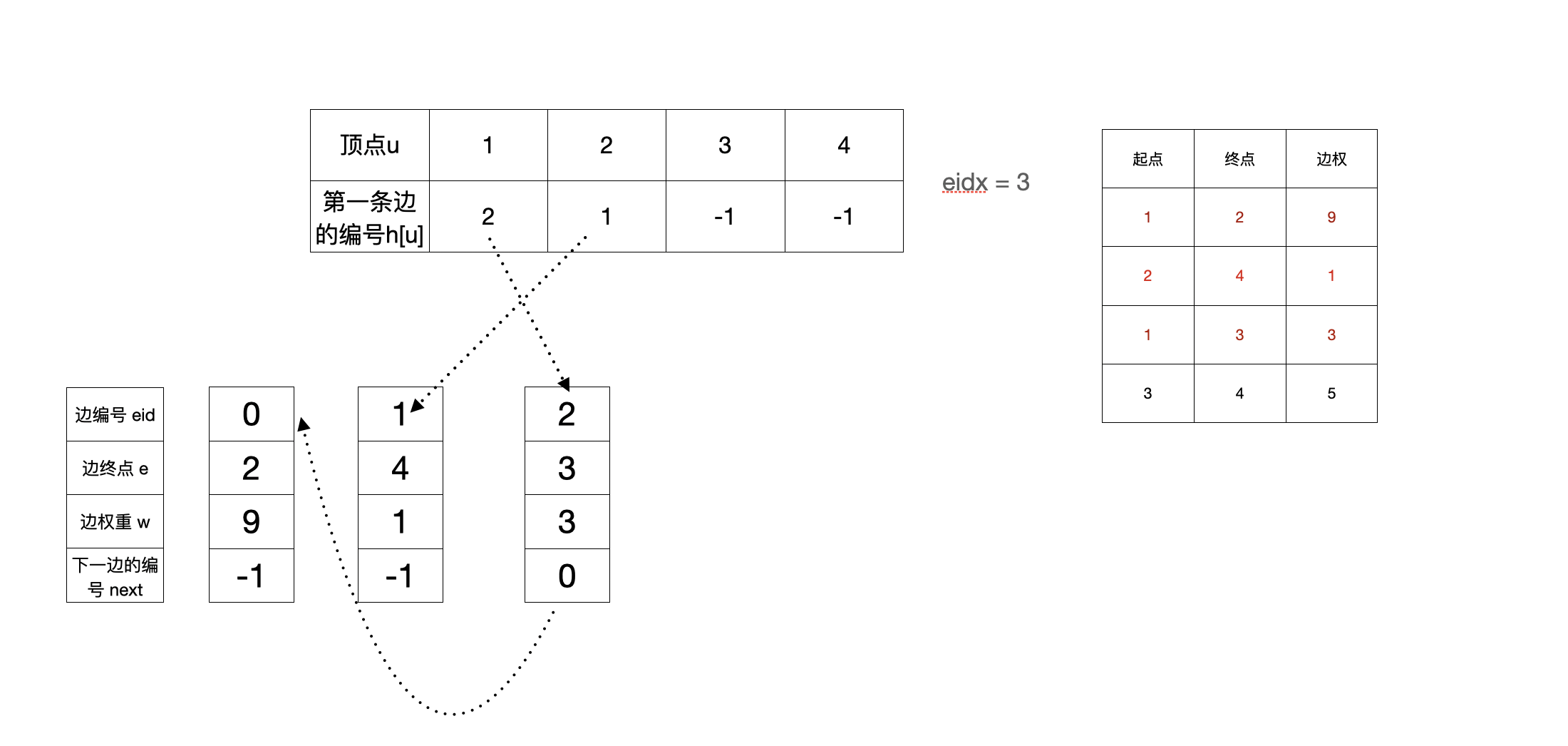
5. 加完第四条边(3,4,5)之后

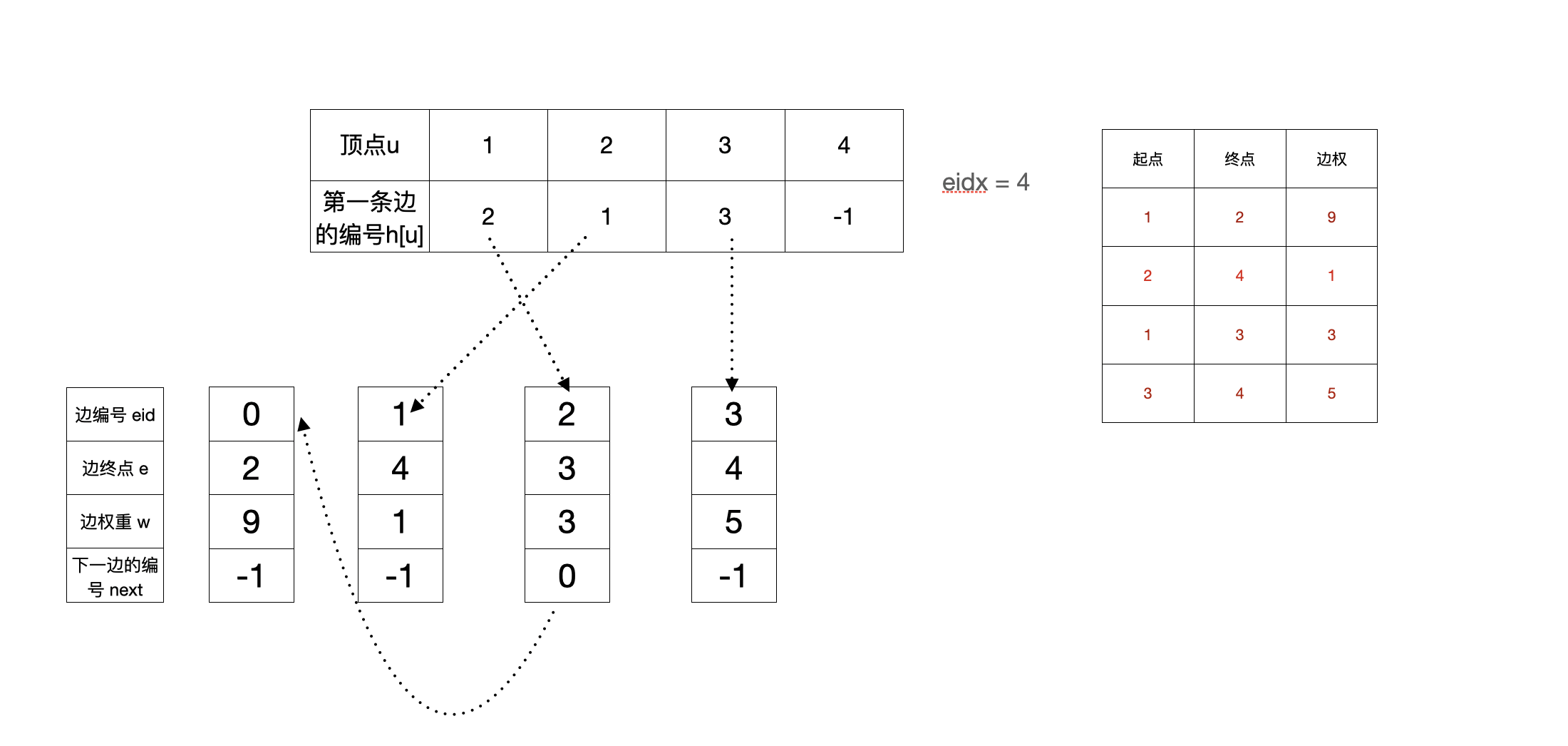
最后是代码及注释

const int N = 1010, M = 1010;

int h[N], e[M], w[M], nxt[M], eidx;

void add(int u, int v, int weight)   // 添加有向边 u->v, 权重为weight
{
    e[eidx] = v;        // 记录边的终点
    w[eidx] = weight;   // 记录边的权重
    nxt[eidx] = h[u];   // 将下一条边指向结点u此时的第一条边
    h[u] = eidx;        // 将结点u的第一条边的编号改为此时的eidx
    eidx++;             // 递增边的编号edix, 为将来使用
}

void iterate(int u)   // 遍历结点u的所有邻边
{
    // 从u的第一条边开始遍历，直到eid==-1为止
    for(int eid = h[u]; eid != -1; eid = nxt[eid])
    {
        int v = e[eid];
        int weight = w[eid];
        cout << u << "->" << v << ", weight: " << weight << endl;
    }
}

int main()
{
    int n, m;
    cin >> n >> m;

    memset(h, -1, sizeof h);  // 初始化h数组为-1
    eidx = 0;                 // 初始化边的编号为0

    while(m--)
    {
        int u, v, weight;
        cin >> u >> v >> weight;
        add(u, v, weight);
    }

    for(int u = 1; u <= n; ++u)
        iterate(u);

    return 0;
}