李超线段树一般用来解决线段交集凸包问题：

• 加入一个一次函数，定义域为 \([l,r]\)
• 给定 \(k\)，求定义域包含 \(k\) 的所有一次函数中，在 \(x=k\) 处取值最大的那个，如果有多个函数取值相同，选编号最小的

看到区间修改，我们按照线段树解决区间问题的常见方法，给每个节点一个懒标记，每个节点 \(i\) 的懒标记都是一条线段，记为 \(l_i\)，表示要用 \(l_i\) 更新该节点所表示的整个区间

考虑现在要插入一条新的线段 \(v\)

第一步要按照线段树的常规方法找到被 \(v\) 完整覆盖的区间

第二步是修改区间内的懒标记，具体如何如何修改？

考虑一个区间的懒标记原来的值为 \(u\)，若原来没有值，则直接为 \(v\)

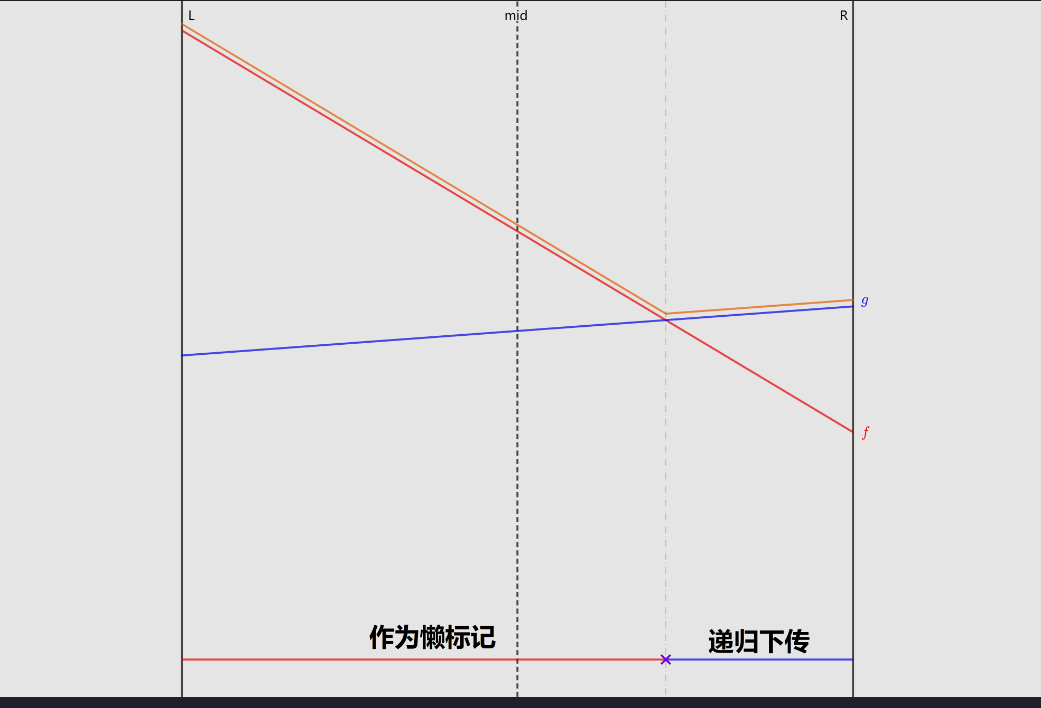
不妨假设 \(u\) 在区间中点处比 \(v\) 更大的情况（若比 \(v\) 小，交换 \(u,v\) 即可）

1. 若在左端点处 \(v\) 更优，那么 \(u\) 和 \(v\) 必然在左儿子内相交，递归更新左儿子
2. 若在右端点处 \(v\) 更优，那么 \(u\) 和 \(v\) 必然在右儿子内相交，递归更新右儿子
3. 若左右端点处 \(u\) 都更优，那么 \(v\) 不可能成为答案，则不需要下传

除了这两种情况之外，还有一种情况是 \(u\) 和 \(v\) 正好相较于中点，在程序实现时可以归入中点不如 \(u\) 的情况，依旧会更新一边

考虑时间复杂度，线段树最多把区间分成 \(\log{L}\) 个小区间，每个小区间更新的时间复杂度时 \(log{L}\) ，总时间复杂度为 \(\log^2{L}\)

代码实现

#include <bits/stdc++.h>
using namespace std;
const int mod1 = 39989, mod2 = 1e9;
const double eps = 1e-9;
typedef pair<double, int> pdi;

int cmp(double x, double y) {
    if (fabs(x - y) < eps) return 0;
    if (x < y) return -1;
    return 1;
}

struct Line {
    int id;
    double k, b;
    Line() {k = 0, b = 0; id = 0;}
    Line(int x_0, int y_0, int x_1, int y_1, int id) {
        this->id = id;
        if (x_0 == y_0) k = 0, b = max(y_0, y_1);
        else k = 1.0 * (y_1 - y_0) / (x_1 - x_0), b = y_0 - k * x_0;
    }
    double calc(int x) { return k * x + b;}
};

bool operator < (const pdi &a, const pdi &b) {
    if (cmp(a.first, b.first) == 0) return a.second > b.second;
    return a.first < b.first;
}

pdi max (const pdi &a, const pdi &b) {
    return a < b ? b : a;
}
int max_x = 0;
struct Segment_Tree {
    int n;
    vector<Line> t;
    Segment_Tree (int n) {
        this->n = n;
        t.resize(4 * n);
    }
    void upd_line (int x, int l, int r, Line v) {
        max_x = max(max_x, x);
        auto &u = t[x];
        int mid = (l + r) / 2;
        int op_mid = cmp(v.calc(mid), u.calc(mid));
        if (op_mid == 1 || (op_mid == 0 && v.id < u.id)) swap(u, v);
        if (l == r) return;
        int op_le = cmp(v.calc(l), u.calc(l)), op_ri = cmp(v.calc(r), u.calc(r));
        if (op_le == 1 || (op_le == 0 && v.id < u.id)) 
            upd_line (x << 1, l, mid, v);
        if (op_ri == 1 || (op_ri == 0 && v.id < u.id))
            upd_line (x << 1 | 1, mid + 1, r, v);
    }

    void upd_pos (int x, int l, int r, int ql, int qr, Line v) {
        max_x = max(max_x, x);
        if (ql <= l && r <= qr) {
            upd_line (x, l, r, v);
            return;
        }
        int mid = (l + r) / 2;
        if (ql <= mid) upd_pos (x << 1, l, mid, ql, qr, v);
        if (qr > mid) upd_pos (x << 1 | 1, mid + 1, r, ql, qr, v);
    }

    pdi query (int x, int l, int r, int pos) {
        max_x = max(max_x, x);
        if (l == r) return pdi(t[x].calc(pos), t[x].id);
        int mid = (l + r) / 2;
        pdi res = pdi(t[x].calc(pos), t[x].id);
        if (pos <= mid) res = max(res, query(x << 1, l, mid, pos));
        else res = max(res, query(x << 1 | 1, mid + 1, r, pos));
        return res;
    }
};

int main() {
    freopen ("P4097.in", "r", stdin);
    freopen ("P4097.out", "w", stdout);
    int n; cin >> n;
    int lastans = 0, cnt = 0;
    Segment_Tree T (mod1 + 1);
    for (int i = 1; i <= n; i++) {
        int op; cin >> op;
        if (op == 0) {
            int x; cin >> x;
            x = (x + lastans - 1) % mod1 + 1;
            // cout << x << endl;
            lastans = T.query(1, 1, mod1, x).second;
            cout << lastans << endl;
        }
        else {
            int x_0, x_1, y_0, y_1; cin >> x_0 >> y_0 >> x_1 >> y_1;
            x_0 = (x_0 + lastans - 1) % mod1 + 1, x_1 = (x_1 + lastans - 1) % mod1 + 1;
            y_0 = (y_0 + lastans - 1) % mod2 + 1, y_1 = (y_1 + lastans - 1) % mod2 + 1;
            // cout << x_0 << " " << y_0 << " " << x_1 << " " << y_1 << endl;
            if (x_0 > x_1) swap(x_0, x_1), swap(y_0, y_1);
            T.upd_pos(1, 1, mod1, x_0, x_1, Line(x_0, y_0, x_1, y_1, ++cnt));
        }
    }
    // cout << max_x << endl;
    return 0;
}