前言
思维训练 1,几乎没有什么算法,枚举 or 搜索 or 二分
- CF1681D Required Length
\(\mathtt{TAGS}\):暴搜 + 剪枝
前置函数
下文中称:\(len(x)\) 为 \(x\) 十进制下的位数。
First. 为什么是搜索
开始看到这道题想到了贪心:每次找出最大的一个数乘上去。
但是很显然:可以先乘一个小的数,使得其中某一位增大大,再乘上最大值是优于直接每次都乘最大值的。例如:\(42 \to 84 \to 672\)。
所以,贪心无法做。
再看一眼数据范围,发现 \(n \le 19\),那么极端一点,对于 \(2\)
每次都只 \(\times 2\),最多也只需要 \(\log_2 10^{19}\) 次。
所以可以尝试一下搜索和剪枝。
Second.如何剪枝
-
可行性剪枝:如果一个数中没有任何一个数字 \(\ge1\),且位数 \(<n\),那么该数一定不能再增加,所以可以剪掉。
-
最优化剪枝:如果当前到达 \(x\) 的次数再加上 \(n - len(x)\)(即要使 \(x\) 的长度到达 \(n\) 最少需要的步数), \(\ge ans\) 那么,一定不是最优解。
-
最优化剪枝2:如果当前到达 \(x\) 的步数 \(\ge\) 之前到达 \(x\) 的步数,那么此时也不可能是最优解。
Third. 无解
如果 \(len(x)\) 怎样都到不了 \(n\) 那么无解。
Code
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
#define int long long
bool check (int x) {
for (int p = x; p; p /= 10) {
if(p % 10 > 1) return 1;
}
return 0;
}
int getlen (int x) {
int len = 0;
for (int p = x; p; p /= 10) len ++;
return len;
}
int n, x;
int ans = 1e18;
map<int, int> res;
void dfs (int x, int cnt) {
int len = getlen(x);
if(!check(x) && len != n) return;
if(!res[x]) res[x] = 1e18;
if(cnt >= res[x] || cnt + (n - len) >= ans) return;
res[x] = cnt;
if(getlen(x) == n) {
ans = min(ans, cnt);
return;
}
for (int p = x; p; p /= 10) {
int num = p % 10;
if(num == 1 || num == 0) continue;
dfs(x * num, cnt + 1);
}
}
signed main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n >> x;
dfs(x, 0);
if(ans == 1e18) cout << -1;
else cout << ans << endl;
return 0;
}
- CF1469D Ceil Divisions
\(\mathtt{TAG}\): 构造
First. \(2\) 的位置
首先,题目要求操作次数在 \(n + 5\) 以内,那么我们的构造的次数肯定是越小越好。
由于序列是一个排列,为了减少次数,不妨让初始的 \(2\) 即为最终的 \(2\),将其余数全部归 \(1\)。
Second. 如何次数更小地形成 \(1\)
从最大数 \(n\) 开始考虑,我们希望尽可能地让这个数让越多数变成 \(1\),又得让剩余的数让它变成 \(1\) 的次数更小。
设 \(x\sim n - 1\) 为,\(n\) 的操作范围,那么操作次数即为:\(n - x + n \log_{x - 1}\)。
当 \(x = \sqrt{n} + 1\) 时,该式取得最小值。
所以,对于 \(\sqrt{n} + 1 \sim n\) 的这一段区间需要的次数即为:\(n - \sqrt{n} + 2\),比区间长度多 \(1\)。
我们只需要一直进行这个操作,使得 \(3 \sim n\) 这段区间全部归 \(1\)。
而每次操作,量级缩小至 \(\sqrt{n}\),而达到 \(3\),极限范围最多只需要 \(4\) 次操作,所以,每次最多多使用 \(4\) 次,所以不会超出 \(n + 5\) 次,所以这种构造方式是可行的。
Code
#include <bits/stdc++.h>
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n;
signed main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
while(t --) {
cin >> n;
vector< pair<int, int> > ans;
for (int i = n; i >= 3; i --) {
int div = ceil(sqrt(i));
for (int j = div + 1; j < i; j ++) ans.push_back({j, i});
ans.push_back({i, div}), ans.push_back({i, div});
i = div + 1;
}
cout << ans.size() << endl;
for (auto opt : ans) cout << opt.first << ' ' << opt.second << endl;
}
return 0;
}
- CF1620C BA-String
\(\mathtt{TAG}\):枚举
First. 缩点
对于一段长度为 \(len\) 连续的 *,它的生成方案数不是 \((k + 1)^{len}\)。为什么?对于该段,长度至多为 \(k \times len\),至少为 \(0\),所以长度一共有 \(len\times k + 1\) 种方案,而所有字符都是相同的,所以方案数仅与长度有关。
于是,不妨将所有连续的 * 所为一个可以生成 \(0 \sim len \times k\) 的特殊 *,后面成为 \(cnt\)。
Second. 定位
考虑字典序最小,肯定是优先展开靠后的 *。
对于后 \(i\) 个 *,他们可以生成的字符串的种类数为 \(fac_i = \prod_{j = i}^{n} cnt_j\)。
找到第一个 \(< x\) 的 \(fac_i\),记为 \(pos\)。
而对于 \(pos - 1\),它每增加一个 b,就会增加 \(fac_{pos}\) 种字符串,所以 \(pos - 1\) 需要展开的个数,即为 \(\frac{x}{fac_{pos}}\)。
对于剩下 \(pos\) 个数,它们应该是后 \(pos\) 个 * 所形成的字符串种第 \(x \bmod fac_{pos}\) 个,按照这种方法接着扫下去,就可以得到每个 * 需要展开的次数。随后,输出即可。
Tips
- \(fac_i\) 可能爆 long long 所以求到第一个 \(> x\) 的 \(fac_i\) 就可以停下了,而前面的
*肯定不能展开。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int , int> pi;
#define endl '\n'
#define int long long
const int N = 2000 + 10;
int n , k , x , tot , tmp;
string s;
int len[N] , cnt[N] , p[N] , fac[N] , to[N];
bool type[N];
int ans[N];
signed main() {
ios::sync_with_stdio(0) , cin.tie(0) , cout.tie(0);
int _;
cin >> _;
while (_--) {
cin >> n >> k >> x >> s;
x--;
s = '.' + s;
tot = tmp = 0;
memset(type, 0, sizeof type), memset(len, 0, sizeof len), memset(fac, 0, sizeof fac);
memset(cnt, 0, sizeof cnt), memset(ans, 0, sizeof ans);
for (int i = 1; i <= n; i++) {
if (s[i] != s[i - 1]) len[++tot] = 1 , type[tot] = (s[i] == '*');
else len[tot]++;
}
for (int i = 1; i <= tot; i++) {
if (type[i]) to[i] = ++tmp , cnt[tmp] = len[i] * k + 1;
}
fac[tmp + 1] = 1;
for (int i = tmp; i >= 1; i--) {
if(fac[i + 1] * 1.0 > (x * 1.0 / (cnt[i] * 1.0))) break; // 防止爆 Long long
fac[i] = fac[i + 1] * cnt[i];
}
for (int i = 2; i <= tmp + 1; i++) {
if(fac[i] == 0) continue;
ans[i - 1] = x / fac[i];
x %= fac[i];
}
for (int i = 1; i <= tot; i++) {
if (!type[i]) {
for (int j = 1; j <= len[i]; j++) cout << 'a'; // 对于连续段 a
} else {
for (int j = 1; j <= ans[to[i]]; j++) cout << 'b'; // 对于连续段 b
}
}
cout << endl;
}
return 0;
}
- CF1550C Manhattan Subarrays
\(\mathtt{TAG}\):暴力、BIT、组合数学
一开始震惊到我了,\(O(n^2 \log_2 n)\) 过了,然后一算发现是 \(O(n \log_2 n)\) 的。
First. 解析坏的三元组
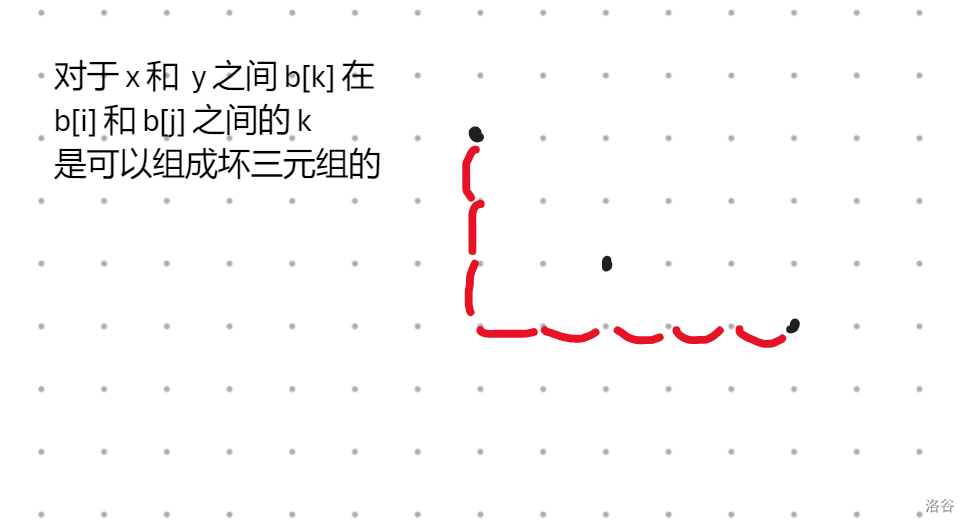
画个图发现,当且仅当 \(x_1 \le x_2 \le x_3\) 且 \(y_1 \ge y_2 \ge y_3\) 或 \(y_1 \le y_2 \le y_3\) 的时候构成坏三元组。
回到题目上,由于每个数的横坐标是下标,所以坏三元组就转化为了一个长度为 \(3\) 不下降或不上升的子序列。
Second. 没有坏三元组的区间
首先不妨进行最暴力的想法,枚举每个区间,看它存不存在坏三元组。
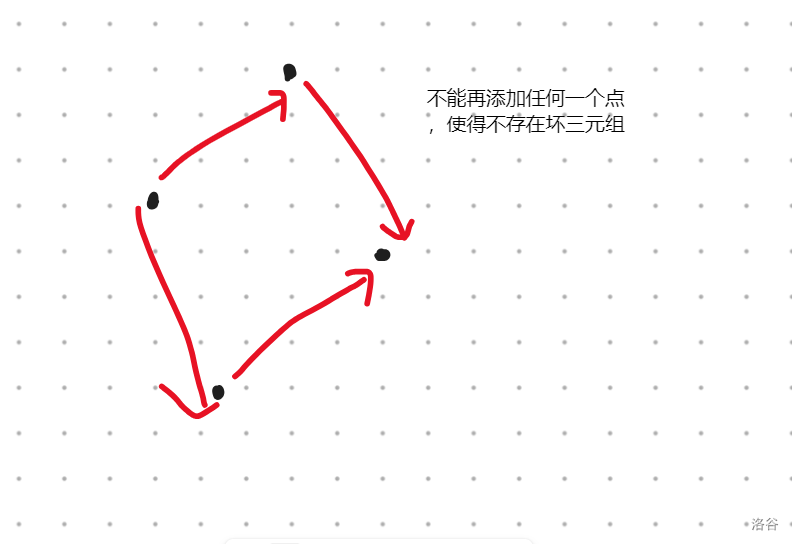
而没有坏三元组的子数组的最长长度为 \(4\)。
证明:
如图,当两个同幅度的子序列相错的时候不能再添加任何一个点。
补充:正确证明是代入 Erdős–Szekeres 定理
Erdős–Szekeres 定理:对于 \(|S| = n \times m + 1\) 的偏序集 \((S,\succ)\) ,一定存在一条长度为 \(m + 1\) 的链或长度为 \(n + 1\) 的反链。
然后代入 \(m + 1 = 3\),得 \(|S| = 5\)。
所以要是其不存在长度为 \(3\) 的链,那么 \(|S| < 5\),所以最大为 \(4\)。
所以对于每个左端点,我们至多会枚举 \(4\) 次。
时间复杂度只有 \(O(n)\)!
Third. 判三元组
蒟蒻太蒟了,看到这种偏序形式就用树状数组了。
先离散化,建 \(3\) 个树状数组,分别维护:权值 \(\le x\) 的点的数量,较大数权值 \(\le x\) 且 \(a_i \ge a_j\) 的二元组数量,较小数权值 \(\le x\) 且 \(a_i \le a_j\) 的二元组数量。
然后就判断点 \(i\) 能否接在之前的一个二元组上,能接上就是坏三元组。
其实暴力更快。
Code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int , int> pi;
#define endl '\n'
const int N = 2e5 + 10;
int n;
int a[N] , b[N];
struct bit {
#define lowbit(x) (x & -x)
int c[N];
void add(int x) {
for (int i = x; i <= n; i += lowbit(i)) c[i]++;
}
void erase(int x) {
for (int i = x; i <= n; i += lowbit(i)) c[i]--;
}
int sum(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += c[i];
return res;
}
};
bit t1 , t2 , t3;
signed main() {
ios::sync_with_stdio(0) , cin.tie(0) , cout.tie(0);
int t;
cin >> t;
while (t--) {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i] , b[i] = a[i];
sort(b + 1 , b + 1 + n);
ll tmp = 0 , ans = 0;
for (int i = 1; i <= n; i++) if (b[i] != b[i - 1]) b[++tmp] = b[i];
for (int i = 1; i <= n; i++) a[i] = lower_bound(b + 1 , b + 1 + tmp , a[i]) - b;//离散化
for (int i = 1; i <= n; i++) {
bool flag = 1;
for (int j = i; j <= n; j++) {
if (t2.sum(a[j]) || t3.sum(n) - t3.sum(a[j] - 1)) {
flag = 0; // 不能暴力清空,会 TLE
for (int k = i; k < j; k++) {
t1.erase(a[k]);
if (t2.sum(a[k]) - t2.sum(a[k] - 1)) t2.erase(a[k]);
if (t3.sum(a[k]) - t3.sum(a[k] - 1)) t3.erase(a[k]);
}
break;
}
ans++;
if (t1.sum(a[j])) t2.add(a[j]);
if (t1.sum(n) - t1.sum(a[j] - 1)) t3.add(a[j]);
t1.add(a[j]);
}
if (!flag) continue;
for (int k = i; k <= n; k++) {
t1.erase(a[k]);
if (t2.sum(a[k]) - t2.sum(a[k] - 1)) t2.erase(a[k]);
if (t3.sum(a[k]) - t3.sum(a[k] - 1)) t3.erase(a[k]);
}
}
cout << ans << endl;
}
return 0;
}