前言
学习差分前一定要先学习前缀和，因为差分就是前缀和的一个逆运算（有点像微分和积分），所以只有先搞清楚前缀和才能明白差分
这里同样也是从一维和二维两个角度去分析差分这个算法
正文
我们要先理清差分的含义：注意关系，这里跟前缀和里举的例子有差别，b的前缀和数组是a（为了便于理解）
-
我们已经知道如果
b数组的前缀和数组为a，那么a[n] = b[1] +b[2] +....+ b[n]。我们称a数组是b的前缀和 -
那么现在我们反过来，我们就称
b数组是a数组的差分
那么现在已知a数组，要求你构造一个b数组，使a数组是b数组的前缀和。
其实对于一维来说构造相当简单，我们让b[n] = a[n] - a[n-1]即可。
但是现在我们不使用这种思路。
我们只需要先明白一点：我们通过a的差分数组b，可以得到a数组本身。其实也可以理解为一种映射。
一维差分
例子引入
这里给出一个差分数组的实际使用案例
我们有a数组和他的差分数组b，现在我们需要给a数组的[l , r]区间内的数都加c。正常情况下我们需要进行一次遍历，给区间每一个数都加上c，时间复杂度为O(n)。
但是上面我们说过，我们可以通过差分数组得到原数组，所以如果我们改动了差分数组，就相当于对原数组做了处理：尽管实际上a数组中的元素都没有改变，但是以后我们都是通过差分数组来得到原数组，而不是通过a来得到原数组（相当于我们通过a创建完他的差分数组后，a就可以不要了，因为b可以映射出a）。
所以现在我们的操作就是：b[l] += c和b[r+1] -=c
-
我们映射
a数组是通过a[n] = b[1] +b[2] +....+ b[n] -
在映射
a数组[1, l-1]时，上面两个位置都没有用到，所以a数组在[1, l-1]区间的值都没有改变 -
在映射
a数组[l, r]时，我们的加法里包含b[l]而不包含b[r]，由于b[l]加了c，所以这一段中的a元素也会随着+c -
在映射
a数组[r+1, .....]时，我们两个位置都用到了，而+=c和-=c的影响会抵消掉，所以后面跟第一段区间一样，元素都没有受到影响 -
综上，只有
[l, r]区间中的a数组元素+c，这便达成了我们的目的。时间复杂度为O(1)
我们从上述的例子中得到了更新的方法，便是b[l] += c和b[r+1] -= c
以更新代构造
我们可以直接通过这种更新方式作为构造差分数组的方法
尽管我们知道a数组里有数据，但是我们现在就假定里面的数据全为0，那么显然，现在他的差分数组里面也全是0，然后假设我们现在开始从第1为更新a数组
由上面的例子我们知道，这种更新可以通过b来完成
- 第一次，我们让
a[1] = a1（放入第一个数据），其实就相当于上面例子中的让a数组[1, 1]区间内的所有数都+a1 - 那么与上个例子一样，我们要做的就是
b[1] += a1和b[2] -= a1 - 第二次让
a[2] = a2，即b[2] += a2和b[3] -= a3 - 推理下去，我们的构造方式就很明显了,遍历
a数组，进行b[n] += a[n]和b[n+1] -= a[n]的步骤。最终就能构造出差分数组b
代码
二维差分
这里的思路与上面的一样，都是通过更新方法代替构造方法。
所以做重要的就是要理清更新方法
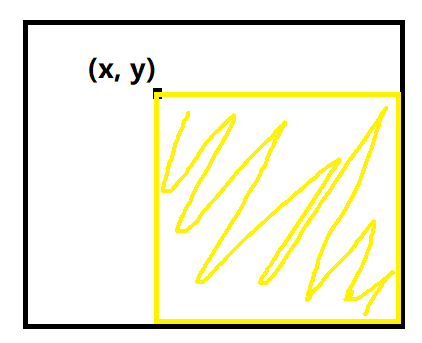
现在假如我们让(x , y) += c，与上面的分析同理，我们不难发现他的作用是将这个点与右下角形成的矩阵中的所有点的数值加c，如下图黄色区域所示
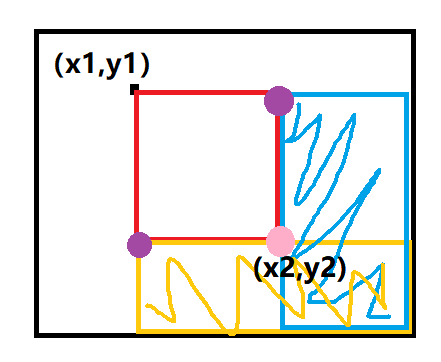
与上面考法相同，这里我们会给出两个坐标，我们需要让这两个坐标形成的矩阵中的所有点数值增加
那么根据更新的方法，我们就不难想到这种更新的策略
- 我们先用
(x1 , y1)更新，让他下面的所有都增加。 - 然后借助两个紫色的点更新减法，让他们下面的区域都减少。
- 由于两个区域重合，所以再更新
(x2+1 , y2+1)增加一份来补全多减的那部分（还是要注意，这是数组，不是连续的，而且我们要包含边界） - 总结为公式:
(x1 , y1) += c，(x1 , y2+1) -= c，(x2+1 , y1) -= c，(x2+1 , y2+1) += c
代码
