1.加减乘除幂运算
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import math
from matplotlib import cm
def visual_2D(array, vmax, vmin):
fig_width = math.ceil(array.shape[1] * 0.5)
fig_length = math.ceil(array.shape[0] * 0.5)
fig, ax = plt.subplots(figsize = (fig_width, fig_length))
sns.heatmap(array,
vmax = vmax,
vmin = vmin,
annot = True,
fmt = '.0f',
square = True,
cmap = 'RdYlBu_r',
linewidth = .5,
cbar = False,
xticklabels = False,
yticklabels = False,
ax = ax)
def visual_1D(array):
fix, ax = plt.subplots()
colors = cm.RdYlBu_r(np.linspace(0, 1, len(array)))
for idx,num in enumerate(array):
circle_idx = plt.Circle((idx, 0 ),
0.5,
facecolor = colors[idx],
edgecolor = 'w')
ax.add_patch(circle_idx)
ax.text(idx, 0, s = str(array[idx]),
horizontalalignment = 'center',
verticalalignment = 'center'
)
ax.set_xlim(-0.6, 0.6 + len(array))
ax.set_ylim(-0.6, 0.6)
ax.axis('off')
ax.set_aspect('equal', adjustable = 'box')
def visual_fx(x_array, y_array, step = False):
fig, ax = plt.subplots(figsize = (5, 5))
ax.plot([-5, 5], [-5, 5], c = 'r', ls = '--', lw = 0.5)
if step:
ax.step(x_array,y_array)
else:
ax.plot(x_array,y_array)
ax.set_xlim(-5, 5)
ax.set_ylim(-5, 5)
ax.axvline(0, c = 'b')
ax.axhline(0, c = 'b')
ax.set_xlabel('x')
ax.set_ylabel('f(x)')
plt.grid(True)
ax.set_aspect('equal', adjustable = 'box')
a = np.arange(-2,3)
b = np.full(5,2)
print('a + b =',a+b)
print('a - b =',a-b)
print('a * b =',a*b)
print('a / b =',a/b)
print('a **b =',a**b)
a + b = [0 1 2 3 4]
a - b = [-4 -3 -2 -1 0]
a * b = [-4 -2 0 2 4]
a / b = [-1. -0.5 0. 0.5 1. ]
a **b = [4 1 0 1 4]
注:二维数组和多维数组和一维数组的运算法则一致
2.广播原则
2.1一维数组和标量
a = np.arange(-2,3)
B = 2
print(f'a = {a} b = {B}')
print('a + 2 =',a+B)
print('a - 2 =',a-B)
print('a * 2 =',a*B)
print('a / 2 =',a/B)
print('a **2 =',a**B)
a = [-2 -1 0 1 2] b = 2
a + 2 = [0 1 2 3 4]
a - 2 = [-4 -3 -2 -1 0]
a * 2 = [-4 -2 0 2 4]
a / 2 = [-1. -0.5 0. 0.5 1. ]
a **2 = [4 1 0 1 4]
2.2一维数组和列向量
一维数组和列向量相加的过程:
a:
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| -2 | -1 | 0 | 1 | 2 |
| -2 | -1 | 0 | 1 | 2 |
| -2 | -1 | 0 | 1 | 2 |
b
| 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 2 | 2 |
| 3 | 3 | 3 | 3 | 3 |
把两个数组扩充到同一维度再相加
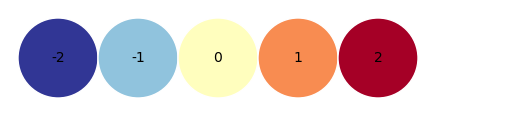
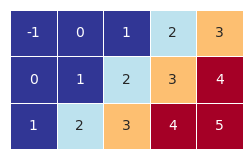
a = np.arange(-2,3)
b = np.arange(1,4)
b = b[:,np.newaxis]
visual_1D(a)
visual_2D(b,4,1)
visual_2D(a+b,4,1)

2.3二维数组和标量
# 二维数组和标量的乘法久相当于:
a = np.array([[j for j in range(-2,3)] for i in range(3)])
b = 2
c = np.full_like(a,b) # 构造一个全为 b 的数组 然后和 a 数组做运算
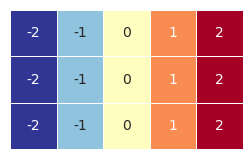
a = np.array([[j for j in range(-2,3)] for i in range(3)])
b = 2
visual_2D(a,2,-2)
visual_2D(a+b,2,-2)
visual_2D(a*b,2,-2)
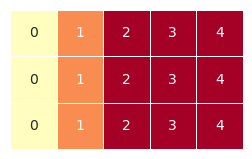
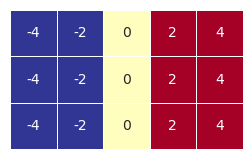
2.4二维数组和一维数组
a = np.array([[j for j in range(-2,3)] for i in range(3)])
b = np.arange(-2,3)
visual_1D(b)
visual_2D(a * b,2,-2)
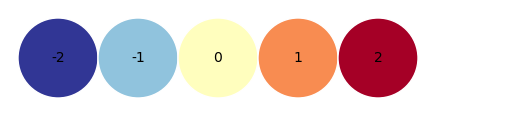
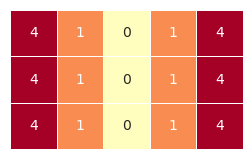
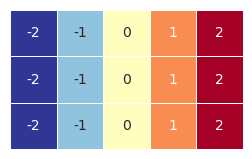
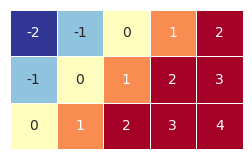
2.4二维数组和列向量
a = np.array([[j for j in range(-2,3)] for i in range(3)])
b = np.arange(0,3)
b = b[:,np.newaxis]
visual_2D(a, 2, -2)
visual_2D(b, 3, 0)
visual_2D(a + b,2,-2)

3.统计运算
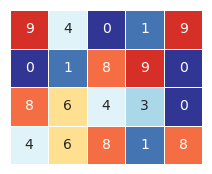
np.random.seed(10)
a = np.random.randint(10,size = (4,5))
visual_2D(a, 10, 0)
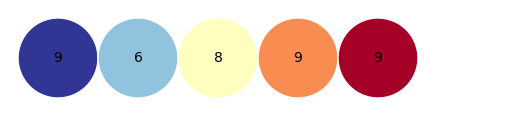
a.max()
visual_1D(a.max(axis = 0)) # axis 用来计算某一个维度最大值
visual_2D(a.max(axis = 1, keepdims = True), 10, 0) # keepdims 用来保持列向量

4.常见函数
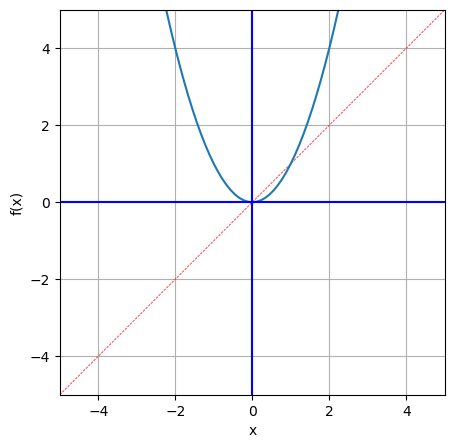
幂函数
x = np.linspace(-5,6,100)
y = np.power(x, 2)
visual_fx(x,y)
# y = np.power(x, 3)
# visual_fx(x,y)
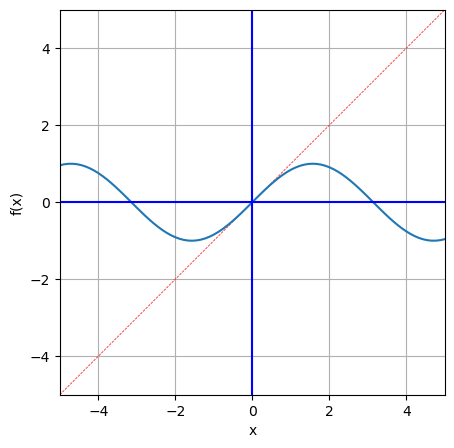
三角函数
x = np.linspace(-5,6,100)
y = np.sin(x)
# y = np.arcsin(x)
# y = np.cos(x)
# y = np.arccos(x)
# y = np.tan(x)
# y = np.arctan(x)
visual_fx(x,y)
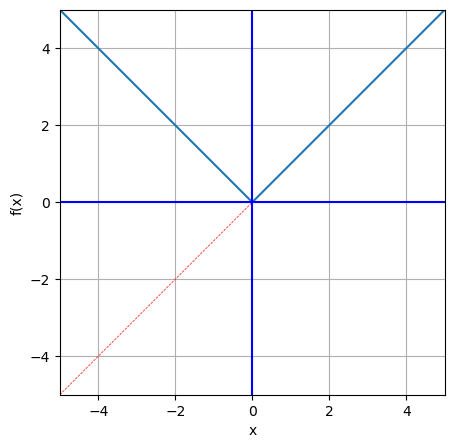
绝对值函数
x = np.linspace(-5,6,100)
y = np.abs(x)
visual_fx(x,y)
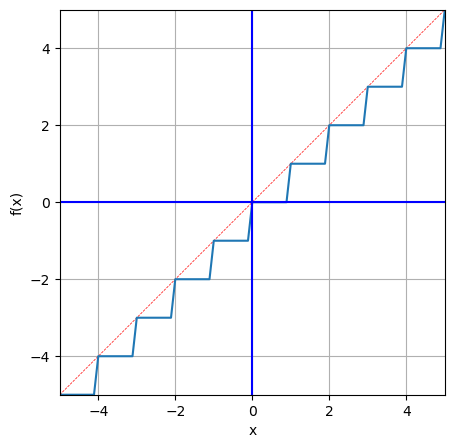
向下取整
x = np.linspace(-5,6,100)
y = np.floor(x)
visual_fx(x,y,step = False)
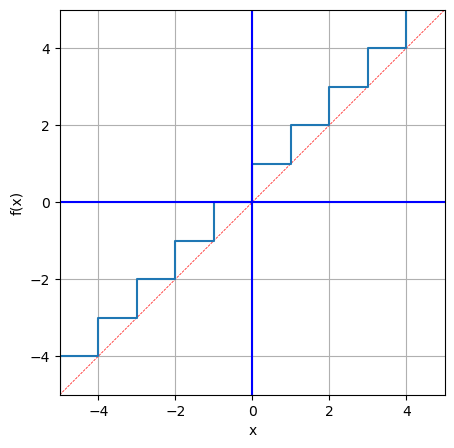
向上取整
x = np.linspace(-5,6,100)
y = np.ceil(x)
visual_fx(x,y,step = True) # 对比step取true和上一个cell step 取 false的区别
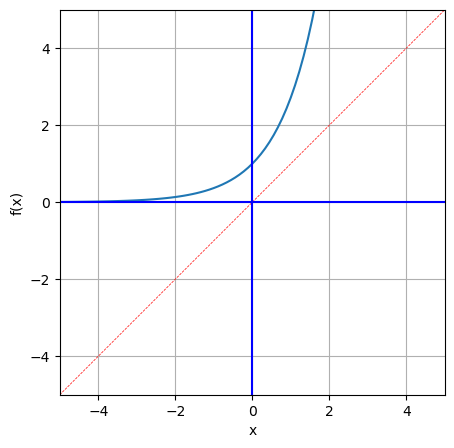
指数函数
x = np.linspace(-5,6,100)
y = np.exp(x)
visual_fx(x,y)
对数函数
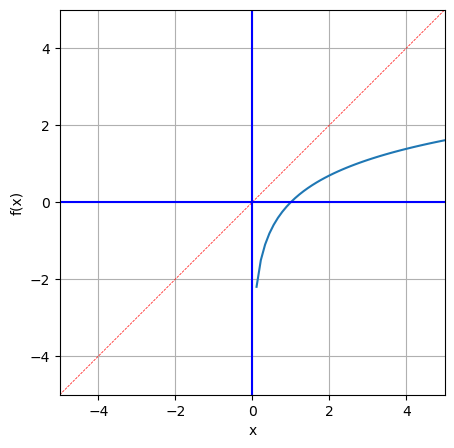
x = np.linspace(-5,6,100)
y = np.log(x)
visual_fx(x,y)
C:\Users\23991\AppData\Local\Temp\ipykernel_13416\2861088069.py:2: RuntimeWarning: divide by zero encountered in log
y = np.log(x)
C:\Users\23991\AppData\Local\Temp\ipykernel_13416\2861088069.py:2: RuntimeWarning: invalid value encountered in log
y = np.log(x)