ABC 223 复盘
[ABC223C] Doukasen
思路解析
根据题目可知,燃烧的总时长肯定不变,所以我们可以直接从头开始遍历找到第一根香使得烧完这根香后的时间会大于总时长的一半,然后加上剩余时间下会烧掉的长度即可。
时间复杂度:一次遍历,\(O(N)\)。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, a[N], b[N];
double t[N], st = 0;
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) {
scanf("%d%d", &a[i], &b[i]);
t[i] = 1.0 * a[i] / b[i];
st += t[i];
}
double ans = 0, s = 0;
for(int i = 1; i <= n; i++) {
if(s + t[i] > st / 2.0) {
ans += ((st / 2.0) - s) * b[i];
break;
}
else ans += a[i], s += t[i];
}
printf("%.15lf", ans);
return 0;
}
[ABC223D] Restricted Permutation
思路解析
题目说的很明白,给定 \(m\) 个约束条件,求排列,很版的一道拓扑。可见这是一道拓扑排序板子,唯一不同的地方就在于一定要字典序最小,我们只需要讲普通拓扑用的普通队列改成优先队列即可。
时间复杂度:由于有优先队列自带 \(\log\) 复杂度,同时每个点最多入队一次,复杂度为 \(O(N \log N)\)。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m, ind[N], d[N], ans[N];
vector<int> g[N];
map<int, int> mp[N];
bool cmp(int x, int y) {
if(d[x] != d[y]) return d[x] < d[y];
else return x < y;
}
int main() {
cin >> n >> m;
for(int i = 1, u, v; i <= m; i++) {
cin >> u >> v;
g[u].push_back(v);
mp[u][v] = 1;
ind[v]++;
}
priority_queue<int, vector<int>, greater<int>> q;
for(int i = 1; i <= n; i++) {
if(ind[i] == 0) d[i] = 1, q.push(i);
}
vector<int> v;
while(!q.empty()) {
int u = q.top(); q.pop();
v.push_back(u);
for(auto it : g[u]) {
ind[it]--;
if(ind[it] == 0) {
d[it] = d[u] + 1;
q.push(it);
}
}
}
for(int i = 1; i <= n; i++) {
ans[i] = i;
if(d[i] == 0) {puts("-1"); return 0;}
}
for(auto it : v) cout << it << ' ';
return 0;
}
[ABC223E] Placing Rectangles
思路解析
根据题目可知,其实三个长方形无非只有以下两种摆放方式。
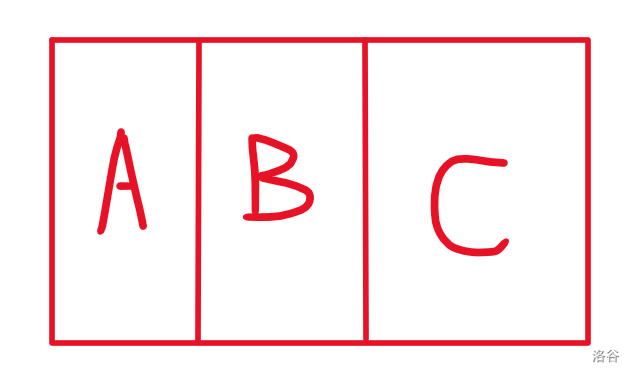
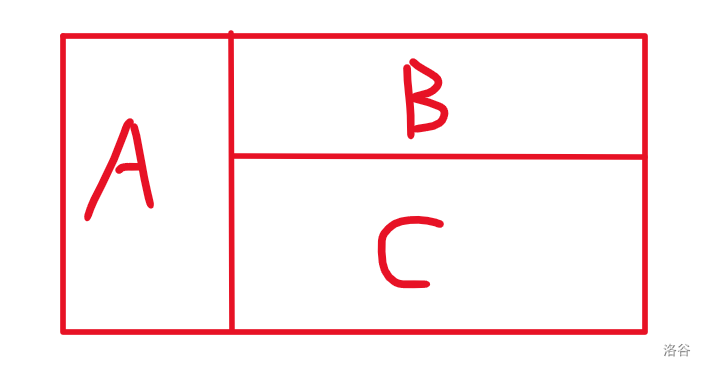
若大长方形长为 \(y\),宽为 \(x\),则我们对于第一种情况就固定住宽,判断能否使长度小于等于长;对于第二种情况同样固定住宽,此时 A 长方形右边空间的长就确定了,就只需要判断 B,C 的宽之和能否小于大长方形的宽即可。
注意大长方形的长宽可以互换,小长方形的顺序可以互换。
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define double long double
ll x, y, a, b, c;
bool check() {
ll ax = ceil((double)a / x), bx = ceil((double)b / x), cx = ceil((double)c / x);
if(ax + bx + cx <= y) return true;
ll yy = y - ax;
if(yy <= 0) return false;
ll by = ceil((double)b / yy), cy = ceil((double)c / yy);
if(by + cy <= x) return true;
return false;
}
int main() {
cin >> x >> y >> a >> b >> c;
bool ans = check();
swap(a, b); ans |= check();
swap(a, c); ans |= check();
swap(x, y); ans |= check();
swap(a, b); ans |= check();
swap(a, c); ans |= check();
if(ans) puts("Yes");
else puts("No");
return 0;
}
[ABC223F] Parenthesis Checking
思路解析
在开始之前,首先我们需要知道合法括号序列的判断方法。我们可以给每个括号打上权值,设左括号权值为 \(1\),右括号权值为 \(-1\),这样一个 \(\texttt{(()())}\) 括号串用数字存下就是 \(1,1,-1,1,-1,-1\),这时我们再给序列计算一下前缀和就成了 \(1,2,1,2,1,0\)。此时我们发现序列有一个性质就是元素全部大于等于 \(0\),同时结尾的元素一定为 \(0\)。而例如我们找一个括号序列 \(\texttt{)()(}\),它的前缀和数组为 \(-1,0,-1,0\),可见虽然结尾是 \(0\),但中间有元素小于 \(0\),因此该括号序列并不合法。
现在我们已经知道了如何通过序列的前缀和数组判断该序列是否合法,接下来我们就考虑如何修改。我们可以先把前缀和数组存下来,然后考虑每一次交换会对这个数组产生怎样的影响。首先,若交换 \(l,r\) 两个位置上的括号,我们可以发现区间 \([1,l-1]\) 和 \([r,n]\) 是没有影响的,真正有影响的只有 \([l,r-1]\) 这个区间。接下来我们分两种情况考虑:
- 若 \(l\) 位上的括号交换前是左括号时,可见由于第 \(l\) 位从 \(1\) 改成了 \(-1\),所以就会对该区间加上 \(-2\) 的权值。
- 若 \(l\) 位上的括号交换前是右括号时,可见由于第 \(l\) 位从 \(-1\) 改成了 \(1\),所以就会对该区间加上 \(2\) 的权值。
最后考虑如何实现,我们需要做到区间求最小值,单点查询,区间加三种操作,可以想到使用线段树维护。注意由于我们存的值是前缀和,所以需要减去 \(l-1\) 位置上的值才能得到正确的值。记得特判 \(l-1=0\) 时的情况。
code
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10, M = 8e5 + 10;
string str;
int n, q, a[N], s[M], t[M];
void push_up(int p) {
int ls = (p << 1), rs = (p << 1) + 1;
s[p] = min(s[ls], s[rs]);
}
void build(int p, int l, int r) {
if(l == r) {
s[p] = a[l];
return;
}
int m = l + ((r - l) >> 1), ls = (p << 1), rs = (p << 1) + 1;
build(ls, l, m);
build(rs, m + 1, r);
push_up(p);
}
void addt(int p, int l, int r, int k) {
s[p] += k;
t[p] += k;
}
void push_down(int p, int l, int r) {
if(!t[p]) return;
int m = l + ((r - l) >> 1), ls = (p << 1), rs = (p << 1) + 1;
addt(ls, l, m, t[p]);
addt(rs, m + 1, r, t[p]);
t[p] = 0;
}
void add(int p, int l, int r, int x, int y, int k) {
if(r < x || l > y) return;
if(l >= x && r <= y) {
addt(p, l, r, k);
return;
}
push_down(p, l, r);
int m = l + ((r - l) >> 1), ls = (p << 1), rs = (p << 1) + 1;
add(ls, l, m, x, y, k);
add(rs, m + 1, r, x, y, k);
push_up(p);
}
int ask(int p, int l, int r, int x, int y) {
if(r < x || l > y) return 2e9;
if(l >= x && r <= y) return s[p];
push_down(p, l, r);
int m = l + ((r - l) >> 1), ls = (p << 1), rs = (p << 1) + 1;
return min(ask(ls, l, m, x, y), ask(rs, m + 1, r, x, y));
}
int main() {
cin >> n >> q;
cin >> str;
str = ' ' + str;
for(int i = 1; i <= n; i++) {
a[i] = a[i - 1];
if(str[i] == '(') a[i]++;
else a[i]--;
}
build(1, 1, n);
while(q--) {
int op, l, r;
cin >> op >> l >> r;
if(op == 1) {
if(str[l] != str[r]) {
if(str[l] == '(') add(1, 1, n, l, r - 1, -2);
else add(1, 1, n, l, r - 1, 2);
swap(str[l], str[r]);
}
}
else {
int tmp = ask(1, 1, n, l - 1, l - 1);
if(l == 1) tmp = 0;
int t1 = ask(1, 1, n, l, r - 1) - tmp, t2 = ask(1, 1, n, r, r) - tmp;
if(t1 >= 0 && t2 == 0) cout << "Yes\n";
else cout << "No\n";
}
}
return 0;
}