[NOI2002] 荒岛野人
题目描述
克里特岛以野人群居而著称。岛上有排列成环行的 \(m\) 个山洞。这些山洞顺时针编号为 \(1,2,\dots ,m\) 。岛上住着 \(n\) 个野人,一开始依次住在山洞 \(C_1,C_2,\dots ,C_n\)中,以后每年,第 \(i\) 个野人会沿顺时针向前走 \(P_i\) 个洞住下来。
每个野人 \(i\) 有一个寿命值 \(L_i\),即生存的年数。
下面四幅图描述了一个有 \(6\) 个山洞,住有三个野人的岛上前四年的情况。三个野人初始的洞穴编号依次为 \(1,2,3\);每年要走过的洞穴数依次为 \(3,7,2\);寿命值依次为 \(4,3,1\)。
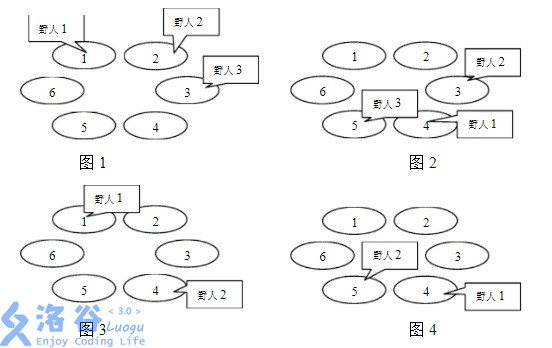
奇怪的是,虽然野人有很多,但没有任何两个野人在有生之年处在同一个山洞中,使得小岛一直保持和平与宁静,这让科学家们很是惊奇。他们想知道,至少有多少个山洞,才能维持岛上的和平呢?
输入格式
第 \(1\) 行为一个整数 \(n(1\leq n\leq 15)\),即野人的数目。
第 \(2\) 行到第 \(N+1\) 每行为三个整数 \(C_i, P_i, L_i (1\leq C_i,P_i \leq 100, 0\leq L_i\leq 10^6 )\),表示每个野人所住的初始洞穴编号,每年走过的洞穴数及寿命值。
输出格式
仅包含一个数 \(M\),即最少可能的山洞数。输入数据保证有解,且 \(M\) 不大于 \(10^6\)。
样例 #1
样例输入
3
1 3 4
2 7 3
3 2 1
样例输出
6
提示
\(1\leq N\leq 15\),\(1\leq C_i,P_i\leq 100\),\(0\leq L_i\leq 10^6\)
保证 \(M\leq 10^6\)
分析
读题
设\(i\)表示第\(i\)个野人 \(x\)表示第\(x\)年
显然
这个野人的位置为
\[(c[i]+p[i]*x) \% m \]那么为了保持小岛的和平安定 对于\(i,j\)两个野人,他们在第\(x\)年 有不等式
\[(c[i]+p[i]*x) \% m \neq(c[j]+p[j]*x) \% m \]嘶~ 他很神奇
我们稍微导亿导
\[(c[i]+p[i]*x)\%m \neq (c[j]+p[j]*x)\%m \]\[c[i]+p[i]*x+m*k_1 \neq c[j]+p[j]*x+m*k_2 \]\[p[i]*x-p[j]*x+m*k_1-m*k_2 \neq c[j]-c[i] \]\[(p[i]-p[j])*x+(k_1-k_2)*m \neq c[j]-c[i] \]他很厉害!他不是一个有形的!
所以你读心经,观自在菩萨,行深般若波罗蜜多时,照见五蕴皆空。
注意,不死不灭,不垢不净,不增不减。
如如不动。
所以万物生于有,有生于无。
他不是一个实体!
你看他像什么
是不是这个↘
这是什么?
裴蜀定理哇
扩展欧几里得求解就完事了...........................吗?
咱这是不等号啊 人家裴蜀定理是等号
那咋办呢
不等式不就是相当于等式取反嘛
我们把导出来的式子换成等号求无解(野人压根遇不到)或求出来的\(最小非负整数解 \geq min(l_i,l_j)\)(其中一个已经死翘翘了)的情况不就完事了嘛~
私货:多导有益于身心健康
code
Elaina's code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define inf 0x3f
#define INF 1e9+100
#define mst(a,b) memset(a,b,sizeof(a))
#define re register
#define Elaina 0
const int N = 10000100;
inline int read(){
int x=0,f=1;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
return x*f;
}
int t,n,m,mod,ans;
int s[N],p[N],l[N];
bool vis[N];
int exgcd(int a,int b,int &x,int &y){
if(!b){
x=1;
y=0;
return a;
}
int res=exgcd(b,a%b,x,y);
int t=x;
x=y;
y=t-a/b*y;
return res;
}
bool check(int m) {
for(int i=1;i<=n;++i){
for(int j=i+1;j<=n;++j){
int a=p[i]-p[j],b=m,c=s[j]-s[i],xx,yy;
int d=exgcd(a,b,xx,yy);
if(c%d){
continue;
}
a/=d,b/=d,c/=d;
if(b<0){
b=-b;
}
xx=(xx*c%b+b)%b;
if(xx<=l[i]&&xx<=l[j]){
return 0;
}
}
}
return 1;
}
main(){
scanf("%lld",&n);
int maxx=0;
for(re int i=1;i<=n;i++){
scanf("%lld%lld%lld",&s[i],&p[i],&l[i]);
maxx=max(maxx,s[i]);
}
for(re int i=maxx;;i++){
if(check(i)){
printf("%lld\n",i);
return Elaina;
}
}
return Elaina;
}
都看到这了,真的不点个赞吗(>ω<*)