学术内容专区,记录一些大悟的东西。
一些待更:分子平均动能
2024.3.26
可逆过程体积功
考虑让压强为 \(p\) 的气体在外界压强为 \(p_外(p_外<p)\) 的情况下膨胀。显然气体会对外界做体积功。假设体积从 \(V_1\) 变为了 \(V_2\),那么对外界做的体积功即为 \(p_外(V_2-V_1)\),于是我们在等压膨胀的情况下对外做的体积功即为对 \(p_外-V\) 这个图像做积分。
又由于 \(pV=nRT\),可得 \(p=\frac{nRT}{V}\),由于 \(p_外<p\),那么我们就让 \(p_外\) 每次减少一个无穷小量,相应的体积也会增加一个无穷小量。这样的一个过程也可以相当于为一个等压膨胀,可以参考下图:
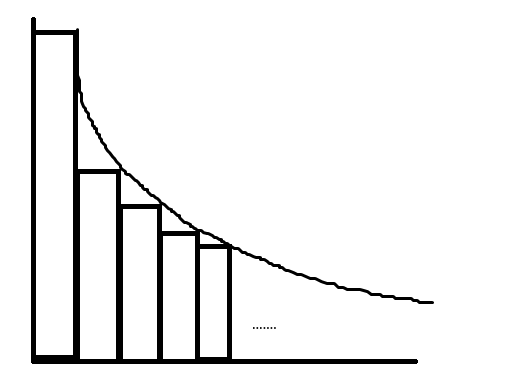
由于减小的是一个无穷小量,因此就相当于对这个图像积分。
写出式子:
\[W_{体积}=\int_{V_1}^{V_2}\delta W=\int_{V_1}^{V_2}p_外\ \mathrm{d}V \]将 \(p_外=\frac{nRT}{V}\) 带入可得:
\[W_{体积}=\int_{V_1}^{V_2}nRT\ \frac{\mathrm{d}V}{V}=nRT\ln\frac{V_2}{V_1} \]于是得到了可逆过程的体积功。
2024.3.23
扭曲烷空间结构
首先显然的中间有一个扭船式的环己烷,然后以这个环己烷为基底,可以发现剩下的键是连接了环己烷的对位碳原子的。
因此将其俯视图画出来。形如这个样子