(1) CF1945D Seraphim the Owl
有 \(n + 1\) 个人站成一排,最开始第 \(i\) 个人在位置 \(i\) 上。
你是第 \(n + 1\) 个人。除你之外,每个人都有两个属性 \(a_i, b_i\)。
每次操作时,假如你在位置 \(i\) 上,那么你需要选择一个位置 \(1 \le j < i\) 并和位置 \(j\) 的人交换位置。代价为 \(a_j + \sum_{k = j + 1}^{i - 1}b_k\)。
求若你最终移动到的位置小于等于 \(m\),总代价最小是多少。
假如我们可以求出 \(f_i\) 表示你从 \(n + 1\) 到达 \(i\) 的最小代价,那么答案即 \(\min_{i = 1}^m f_i\)。
我们可以画图模拟一下跟前面人交换位置的过程:
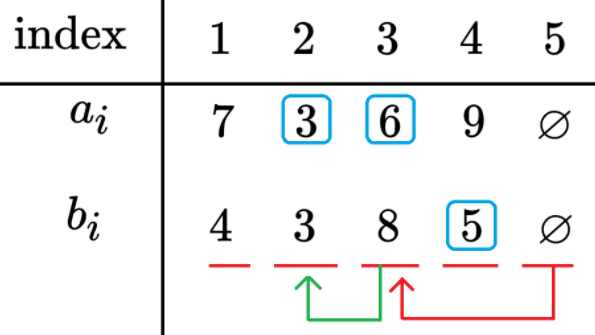
那么答案为蓝色框起的数之和 \(3 + 6 + 5 = 14\)。
可以发现,若某个人 \(j\) 是和你交换过位置的,那么 ta 的贡献为 \(a_i\)。否则若是被你跨过的,ta 的贡献为 \(b_i\)。
每个人是否选择和你交换是你可以选择的,所以对于每个人,我们看两种方式的代价 \(a_i\) 和 \(b_i\) 的大小,并取代价较小的方案即可。
回到我们求解 \(f_i\) 的任务。由于我们最终到了位置 \(i\) 上,所以我们必定会和第 \(i\) 个人交换位置。那么实际上我们一定会消耗代价 \(a_i\)。但是对于后面的人,就可以用上面的策略进行了。所以 \(f_i = a_i + \sum_{j=i+1}^n \min(a_j, b_j)\)。