本题解中不区别长度和宽度的区别,它们在本题解中指的是同一个东西。
本题解做法用到单调栈。
看这个特殊性质好像是让我们在高度上进行研究一下。
子任务 \(4\) 的特殊性质是想让你搞明白在一个矩形中如何计算其内部的矩形个数。
下面是一个 \(4\times 5\) 大小的矩形。

先来不考虑高度的影响,我们观察任一行的单位矩形,来统计该行的矩形。
这样的问题可以看成是一条线段让你截出若干个不同的线段,每个格子相当于一个点,我们统计合法的左右端点对数即可。
第 \(1\) 个格子作为左端点可以有第 \(1\),\(2\),\(\dots\),\(5\) 个格子作为右端点与其匹配。
第 \(2\) 个格子则有 \(2\),\(\dots\),\(5\)。
以此类推,设该行的长度为 \(w\),我们可以在该行中找出 \(\sum\limits_{i=1}^wi=\frac{w\times(w+1)}{2}\) 个矩形。
接着我们来考虑高度的影响,高度上与长度是独立的,设这个矩形的高为 \(h\),长度为 \(w\),容易发现这个矩形内有 \(\sum\limits_{i=1}^{w}i \times \sum\limits_{i=1}^{h}i=\frac{w\times(w+1)\times h\times (h+1)}{4}\)。
我们可以将这些矩形先看作一个整体,按照高度划分成若干的矩形进行统计。类似于下图。
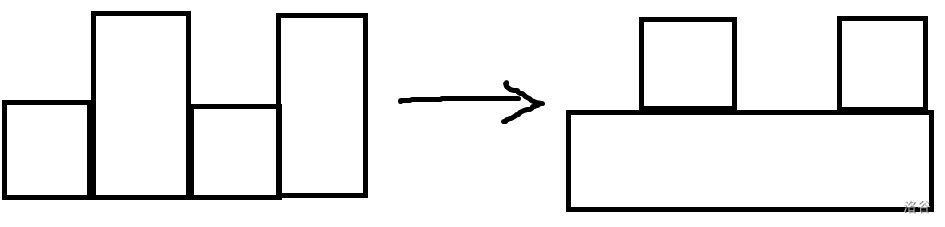
这样我们维护一个单调栈,栈里面存放的是一个若干递增的矩形的整体,当遇到一个比栈中最高的矩形要矮的矩形时或最后的时候进行出栈统计。
这里的划分是指在维护过程中切掉突出的那一块,并将答案更新,使得最后的结果正确。
不可以只计算突出的部分内部的矩形个数,会少一些突出部分与下面一些部分结合的矩形。
可以采用容斥的方法计算,我这里把容斥剩余的部分给推了一下放代码里面,与直接容斥写法不同。
注意 long long 和取模的问题。
代码如下。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
constexpr int MAXN=1e5+10,MOD=1e9+7,inv2=500000004;
int n,h[MAXN],w[MAXN];
ll sum[MAXN],ans;
int s[MAXN],p;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d",&h[i]);//高度
}
for(int i=1;i<=n;++i){
scanf("%d",&w[i]);//宽度
sum[i]=sum[i-1]+w[i];
}
for(int i=1;i<=n;++i){
while(p&&h[i]<h[s[p]]){
if(h[s[p-1]]>=h[i]){
ans=(ans+
((((((sum[i-1]-sum[s[p]-1])%MOD)*
((sum[i-1]-sum[s[p]-1]+1)%MOD))%MOD)*inv2)%MOD)*
(((((((ll)h[s[p]]-h[s[p-1]])%MOD)*
(((ll)h[s[p]]+h[s[p-1]]+1)%MOD))%MOD)*inv2)%MOD)%MOD
)%MOD;
--p;
}
else{
ans=(ans+
((((((sum[i-1]-sum[s[p]-1])%MOD)*
((sum[i-1]-sum[s[p]-1]+1)%MOD))%MOD)*inv2)%MOD)*
(((((((ll)h[s[p]]-h[i])%MOD)*
(((ll)h[s[p]]+h[i]+1)%MOD))%MOD)*inv2)%MOD)%MOD
)%MOD;
h[s[p]]=h[i];
}
}
if(!p||h[i]>h[s[p]]){s[++p]=i;}
}
while(p){
ans=(ans+
((((((sum[n]-sum[s[p]-1])%MOD)*
((sum[n]-sum[s[p]-1]+1)%MOD))%MOD)*inv2)%MOD)*
(((((((ll)h[s[p]]-h[s[p-1]])%MOD)*
(((ll)h[s[p]]+h[s[p-1]]+1)%MOD))%MOD)*inv2)%MOD)%MOD
)%MOD;
--p;
}
printf("%lld\n",ans);
return 0;
}