前话
貌似别人都是使用并查集维护的方法,然而由于排序、最短路等算法瓶颈,以下令 \(n\) 和 \(m\) 同阶,总的时间复杂度依然是 \(\Theta(n \log n)\) 的,那么并查集是否有点大材小用了。事实上,在建完最短路径树后,我给出了两种带 \(\log\) 的数据结构完成此题。
题目分析
翻译里已经把问题抽象出来了,这里不过多赘述。考虑到从 \(1\) 到任意结点的最短路是唯一的,说明将所有最短路径保留,删去其它边,一定能形成一棵树,这棵树就是最短路径树。我们称保留下来的边为树边,删去的边为非树边。
题目要求不经过原来最短路上最后一条边的最短路,也就是删去 \(u\) 和 \(fa[u]\) 之间的树边后,通过剩余的树边非树边到达 \(u\) 的最短路。很容易想到,必然要经过一条非树边,而且最多只经过一条非树边。前者考虑连通性证明显然,后者有如下证明:
证明:
假设删去 \(u\) 和 \(fa[u]\) 之间的树边后,经过了两条非树边得到最短路径是 \(1 \stackrel{\color{blue}{\texttt{树边}}}{\color{blue}{\longrightarrow}} xym \stackrel{\color{red}{\texttt{非树边}}}{\color{red}{\longrightarrow}} xym' \stackrel{\color{blue}{\texttt{树边}}}{\color{blue}{\longrightarrow}} yzh \stackrel{\color{red}{\texttt{非树边}}}{\color{red}{\longrightarrow}} yzh' \stackrel{\color{blue}{\texttt{树边}}}{\color{blue}{\longrightarrow}} u\),那么根据最短路径树的相关性质,有路径 \(1 \stackrel{\color{blue}{\texttt{树边}}}{\color{blue}{\longrightarrow}} yzh \stackrel{\color{red}{\texttt{非树边}}}{\color{red}{\longrightarrow}} yzh' \stackrel{\color{blue}{\texttt{树边}}}{\color{blue}{\longrightarrow}} u\) 比以上路径更短,原假设不成立,经过多条非树边情况同理。证毕。
考虑走的过程,容易知道 \(yzh\) 不能是 \(u\) 子树里的节点,因为如果是的话,走到 \(yzh\) 的时候就经过了 \(fa[u] \rightarrow u\) 这条边,与题意不符。另外,\(yzh'\) 是 \(u\) 子树里的结点(当然 \(u\) 也属于 \(u\) 的子树里),这样才能一路向上走走到 \(u\)。放张图吧。
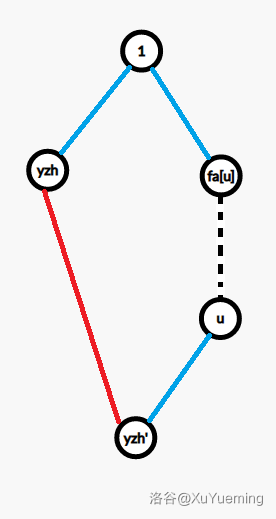
记 \(d_u\) 为 \(u\) 的最短路长度,即 \(1 \rightarrow u\) 这条路径的距离,记 \(\operatorname{dist}(u, v)\) 为 \(u\) 经过一条非树边走到 \(v\) 的长度。
所以先跑一遍最短路建出最短路径树。考虑第一遍深搜,枚举 \(yzh\) 连出的所有非树边 \(yzh \rightarrow yzh'\),在 \(yzh'\) 上打上一个标记 \(d_{yzh} + \operatorname{dist}(yzh, yzh')\),这样在第二遍深搜的时候,就可以把子树的标记不断向上传递、合并,把子树的所有标记加上到父节点的距离,再和父节点合并,就是模拟 \(yzh'\) 到 \(u\) 的过程。然后得到答案的时候就是取出标记里最小的那个就行了。但是发现这样存在一个问题,就是不能保证不会出现上文提到的 \(yzh\) 不能是 \(u\) 子树里的节点这个要求,也就是在不断向上传递的时候,有可能传递到了 \(yzh\) 甚至 \(yzh\) 的祖先,这显然会造成问题。解决方法就是将标记增加一个信息变为 \((d_{yzh} + \operatorname{dist}(yzh, yzh'), yzh)\),这样每次取出当前最小值时,发现 \(yzh\) 不满足要求,就将这个标记删除。判断合法可以在第一遍深搜时处理出 dfs 序判断。这个过程套路化地有以下两种方法解决。
1. 左偏树 + 懒惰标记
合并、整体加、删除最小值、获取最小值,明显是可合并堆的范畴啊,这里使用左偏树解决。顺带一提,由于有整体加这个操作,不好使用启发式合并,所以老老实实写左偏树吧。
2. 线段树
什么?你竟然不会使用左偏树,那就快乐地打线段树吧!
为什么要合并?我们只用知道整个子树的信息啊,所以可以在另外记一个信息的 dfs 序,然后树上问题有变成序列上的问题了,区间加、求最小值,使用线段树维护,删除的时候将其赋成 \(\infty\) 就能不会对之后产生影响。注意区分两个 dfs 序的区别。
代码(已略去快读快写,码风清新,注释详尽)
1. 左偏树 + 懒惰标记
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast", "inline", "-ffast-math")
//#pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
#define debug(a) cerr << "Line: " << __LINE__ << " " << #a << endl
#define print(a) cerr << #a << "=" << (a) << endl
#define file(a) freopen(#a".in", "r", stdin), freopen(#a".out", "w", stdout)
#define main Main(); signed main(){ return ios::sync_with_stdio(0), cin.tie(0), Main(); } signed Main
using namespace std;
#include <cstring>
#include <queue>
int n, m;
int ans[100010];
struct Graph{
struct node{
int to, len, nxt;
} edge[200010 << 1];
int eid, head[100010];
inline void add(int u, int v, int w){
edge[++eid] = {v, w, head[u]};
head[u] = eid;
}
node & operator [] (const int x){
return edge[x];
}
} xym, yzh;
// 一个是原图,一个是最短路径树
// 最短路,父亲,和父亲的距离
int dist[100010], fr[100010], lenfa[100010];
template <class T> using MinHeap = priority_queue<T, vector<T>, greater<T> >;
// dfs 序判断子树
int L[100010], R[100010], timer;
int root[100010]; // u 在左偏树里的结点
int fa[400010], dis[400010], lson[400010], rson[400010]; // 左偏树
int lazy[400010]; // 左偏树懒惰标记
pair<int, int> val[400010]; // 信息
int pcnt;
int NewNode(pair<int, int> v){
return val[++pcnt] = v, fa[pcnt] = pcnt;
}
void pushtag(int u, int tag){
val[u].first += tag;
lazy[u] += tag;
}
void pushdown(int u){
if (lazy[u] == 0) return;
if (lson[u]) pushtag(lson[u], lazy[u]);
if (rson[u]) pushtag(rson[u], lazy[u]);
lazy[u] = 0;
}
int combine(int a, int b){
if (!a || !b) return a | b;
if (val[a] > val[b]) swap(a, b);
pushdown(a), rson[a] = combine(rson[a], b);
if (dis[lson[a]] < dis[rson[a]]) swap(lson[a], rson[a]);
dis[a] = dis[rson[a]] + 1;
return a;
}
// 第一遍 dfs
void dfs(int now){
L[now] = ++timer; // 记录 dfs 序
for (int i = xym.head[now]; i; i = xym[i].nxt){ // 枚举 yzh -> yzh' 这条非树边
int to = xym[i].to, len = xym[i].len;
if (fr[to] == now && len == lenfa[to]) continue; // 这里要很小心地判断树边
int node = NewNode({dist[now] + len, now});
if (!root[to]) root[to] = node;
else root[to] = combine(root[to], node);
}
for (int i = yzh.head[now]; i; i = yzh[i].nxt) dfs(yzh[i].to);
R[now] = timer;
}
// 第二遍 dfs
void redfs(int now){
for (int i = yzh.head[now]; i; i = yzh[i].nxt){ // 把子树标记合并过来
int to = yzh[i].to, len = yzh[i].len;
redfs(to);
if (!root[to]) continue;
pushtag(root[to], len);
if (!root[now]) root[now] = root[to];
else root[now] = combine(root[now], root[to]);
}
// 弹出不符合的标记
while (root[now] && L[now] <= L[val[root[now]].second] && L[val[root[now]].second] <= R[now]){
if (lson[root[now]] == 0 && rson[root[now]] == 0){
root[now] = 0;
} else {
root[now] = combine(lson[root[now]], rson[root[now]]);
}
}
// 统计答案
if (root[now]) ans[now] = val[root[now]].first;
else ans[now] = -1;
}
// 迪迦哥斯拉算法(逃
// 迪杰斯特拉求最短路,并建出最短路径树
void build(){
memset(dist, 0x3f, sizeof dist);
MinHeap<pair<int, int> > Q; Q.push({dist[1] = 0, 1});
while (!Q.empty()){
auto [ndis, now] = Q.top(); Q.pop();
if (dist[now] < ndis) continue;
for (int i = xym.head[now]; i; i = xym[i].nxt){
int to = xym[i].to, len = xym[i].len;
if (dist[to] > dist[now] + len){
Q.push({dist[to] = dist[now] + len, to});
fr[to] = now, lenfa[to] = len;
}
}
}
for (int i = 2; i <= n; ++i) yzh.add(fr[i], i, lenfa[i]);
}
signed main(){
read(n, m);
for (int i = 1, u, v, w; i <= m; ++i) read(u, v, w), xym.add(u, v, w), xym.add(v, u, w);
build(), dfs(1), redfs(1);
for (int i = 2; i <= n; ++i) write(ans[i], '\n');
return 0;
}
2. 线段树
//#pragma GCC optimize(3)
//#pragma GCC optimize("Ofast", "inline", "-ffast-math")
//#pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
#define debug(a) cerr << "Line: " << __LINE__ << " " << #a << endl
#define print(a) cerr << #a << "=" << (a) << endl
#define file(a) freopen(#a".in", "r", stdin), freopen(#a".out", "w", stdout)
#define main Main(); signed main(){ return ios::sync_with_stdio(0), cin.tie(0), Main(); } signed Main
using namespace std;
#include <cstring>
#include <queue>
#include <vector>
const int inf = 0x3f3f3f3f;
int n, m;
int ans[100010];
struct Graph{
struct node{
int to, len, nxt;
} edge[200010 << 1];
int eid, head[100010];
inline void add(int u, int v, int w){
edge[++eid] = {v, w, head[u]};
head[u] = eid;
}
node & operator [] (const int x){
return edge[x];
}
} xym, yzh;
// 一个是原图,一个是最短路径树
// 最短路,父亲,和父亲的距离
int dist[100010], fr[100010], lenfa[100010];
template <class T> using MinHeap = priority_queue<T, vector<T>, greater<T> >;
// dfs 序判断子树
int L[100010], R[100010], timer;
// 信息的 dfs 序
int infoL[100010], infoR[100010], infot;
vector<pair<int, int> > info[100010];
pair<int, int> val[400010]; // 注意这里要开大一些
struct Segment_Tree{
#define lson (idx << 1 )
#define rson (idx << 1 | 1)
struct Info{
pair<int, int> val;
int pos;
Info operator + (const Info & o) const {
if (val.first == inf) return o;
if (o.val.first == inf) return *this;
if (val.first < o.val.first) return *this;
return o;
}
Info operator + (const int o) const {
if (val.first == inf) return *this;
return {{val.first + o, val.second}, pos};
}
};
// 信息
struct node{
int l, r;
Info info;
int tag;
} tree[400010 << 2];
void pushup(int idx){
tree[idx].info = tree[lson].info + tree[rson].info;
}
void build(int idx, int l, int r){
tree[idx] = {l, r, {{inf, -1}, -1}, 0};
if (l == r) return tree[idx].info = {val[l], l}, void();
int mid = (l + r) >> 1;
build(lson, l, mid), build(rson, mid + 1, r), pushup(idx);
}
void pushtag(int idx, const int t){
tree[idx].info = tree[idx].info + t;
tree[idx].tag = tree[idx].tag + t;
}
void pushdown(int idx){
if (!tree[idx].tag) return;
pushtag(lson, tree[idx].tag), pushtag(rson, tree[idx].tag);
tree[idx].tag = 0;
}
Info query(int idx, int l, int r){
if (tree[idx].l > r || tree[idx].r < l) return {{inf, -1}, -1};
if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].info;
return pushdown(idx), query(lson, l, r) + query(rson, l, r);
}
void modify(int idx, int l, int r, const int t){
if (tree[idx].l > r || tree[idx].r < l) return;
if (l <= tree[idx].l && tree[idx].r <= r) return pushtag(idx, t);
pushdown(idx), modify(lson, l, r, t), modify(rson, l, r, t), pushup(idx);
}
void erase(int idx, int p){
if (tree[idx].l > p || tree[idx].r < p) return;
if (tree[idx].l == tree[idx].r) return tree[idx].info = {{inf, -1}, -1}, void();
pushdown(idx), erase(lson, p), erase(rson, p), pushup(idx);
}
#undef lson
#undef rson
} tree;
// 第一遍 dfs
void dfs(int now){
L[now] = ++timer; // 记录 dfs 序
for (int i = xym.head[now]; i; i = xym[i].nxt){ // 枚举 yzh -> yzh' 这条非树边
int to = xym[i].to, len = xym[i].len;
if (fr[to] == now && len == lenfa[to]) continue; // 这里要很小心地判断树边
info[to].push_back({dist[now] + len, now});
}
for (int i = yzh.head[now]; i; i = yzh[i].nxt) dfs(yzh[i].to);
R[now] = timer;
}
// 其实也算一次深搜,记录标记的 dfs 序
void prework(int now){
infoL[now] = infot + 1;
for (auto x: info[now]) val[++infot] = x;
for (int i = yzh.head[now]; i; i = yzh[i].nxt) prework(yzh[i].to);
infoR[now] = infot;
}
// 第二遍 dfs
void redfs(int now){
if (infoL[now] > infoR[now]) return;
for (int i = yzh.head[now]; i; i = yzh[i].nxt){ // 把子树标记合并过来
int to = yzh[i].to, len = yzh[i].len;
redfs(to), tree.modify(1, infoL[to], infoR[to], len);
}
// 弹出不符合的标记
while (true){
Segment_Tree::Info res = tree.query(1, infoL[now], infoR[now]);
if (res.val.first == inf || res.pos == -1) break;
if (L[now] <= L[res.val.second] && L[res.val.second] <= R[now]){
tree.erase(1, res.pos);
continue;
}
// 统计答案
ans[now] = res.val.first;
break;
}
}
// 迪迦哥斯拉算法(逃
// 迪杰斯特拉求最短路,并建出最短路径树
void build(){
memset(dist, 0x3f, sizeof dist);
MinHeap<pair<int, int> > Q; Q.push({dist[1] = 0, 1});
while (!Q.empty()){
auto [ndis, now] = Q.top(); Q.pop();
if (dist[now] < ndis) continue;
for (int i = xym.head[now]; i; i = xym[i].nxt){
int to = xym[i].to, len = xym[i].len;
if (dist[to] > dist[now] + len){
Q.push({dist[to] = dist[now] + len, to});
fr[to] = now, lenfa[to] = len;
}
}
}
for (int i = 2; i <= n; ++i) yzh.add(fr[i], i, lenfa[i]);
}
signed main(){
read(n, m);
for (int i = 1, u, v, w; i <= m; ++i) read(u, v, w), xym.add(u, v, w), xym.add(v, u, w);
for (int i = 2; i <= n; ++i) ans[i] = -1;
build(), dfs(1), prework(1), tree.build(1, 1, infot), redfs(1);
for (int i = 2; i <= n; ++i) write(ans[i], '\n');
return 0;
}
总结 & 后话
考场上没想到可以将长度拆开来算,也就是计算答案的时候不用一步一步加与父亲的长度加上去,而是用 \(d_{yzh'} - d_u\) 计算,这样对于 \(u\) 来说,\(d_u\) 是确定的,要求的就是 \(\min \lbrace d_{yzh} + \operatorname{dist}(yzh, yzh') + d_{yzh'} \rbrace\),这样可以愉快地用启发式合并秒了啊!但是练习一道左偏树懒惰标记的题目,感觉也颇有收获呢。但是但是,线段树无敌爱敲。