标签：int 查集合并 fa maxn find

并查集

并查集是一种可以动态维护若干个不重叠集合，并且支持合并与查询的数据结构，主要用于处理不相交集合的的合并关系。

为了具体实现并查集这种数据结构，首先我们需要定义集合的表示方法。在并查集中，我们采用"代表元"法,即为每一个集合选择一个固定的元素，作为整个集合的代表。

其次，我们需要定义归属关系的表示方法。

第一种思路：维护一个数组 \(f\) 用 \(f[x]\) 来表示元素 \(x\) 所在集合的“代表”。这可以快速的查询元素 \(x\) 的所属集合，但在修改时需修改大量的 \(f\) 值，效率极低。

第二种思路：使用一个树形结构存储存储每个集合，树上的每个点都是一个元素，树根是集合的代表元素。 整个并查集实际上是一个森林。我们仍可维护一个数组 \(fa[]\) 来模拟这个森林，用 \(fa[x]\) 表示 \(x\) 的父节点。特别的，令树根的 \(fa\) 值为它本身。

如此一来，在合并两个集合时，只需令其中一个数根成为另一个树的子节点。不过在查询时，需从该元素开始不断递归的寻找集合的代表元素。为了提高查询的效率，并查集引入了路径压缩与按秩合并两种思想，下文中将会提到。

本文将包括：

并查集

1.1 并查集的基础操作

主要包括1.初始化 2.查找 3.合并 4.统计

(1.初始化

定义一个数组 \(fa[]\) , \(fa[i]\) 是 \(i\) 元素所指向的父节点，开始时每个元素都是一个集合（即都指向自己）

int N                               //N为元素个数
int init_set(int N){
    for（int i=1;i<=N;i++）
        fa[i]=i;                    //初始化指向自己 
}

（2.查找

查找元素的集合的“代表”，是一个递归的过程，直到元素的值与自己相同时（即当 \(fa[i]==i\) 时），这里给出初级的查找函数，后将用路径压缩优化。

int x;                         //将要查找的元素x
int find(int x){
    if(fa[x]==x) 
        return x;              //递归出口，即元素与其父节点相等
    return find(fa[x]);        //否则递归向上寻找根节点
}

（3.合并

合并两元素的集合，即将一棵树变为另一棵树的子树，这里给出初级的合并函数，后将用按秩合并优化。

int x,y;                         //将要合并的元素x,y
void join(int x,int y){          
    int f1=find(x),f2=find(y);   //取出两棵树的根节点
    if(f1!=f2)                   //若不在同一集合
        fa[f1]=f2;               //则将x所在的树变为y所在的树的子树
}

(4.统计

由于根节点的 \(fa\) 数组指向自己，故当有 \(n\) 个 \(i\) 满足 \(fa[i]==i\) 时，并查集便有 \(i\) 个。

int N;                       //共有N个元素
int sum(){
    int num;                 //共有num个集合
    for(int i=1;i<=N;i++)
         if(fa[i]==i)        //满足条件
             num++;
    return num;
}

1.2合并的优化（按秩合并）

首先，我们要了解秩的定义。

秩有两种定义方式，一种为树的高度，可用来优化合并（在未进行路径压缩时），另一种定义在路径压缩后给出。

为何以树的高度为秩进行合并优化，下面给出正确性证明：

在下图的两棵树中，选择将⑥树（即矮树）合并到①树（高树上）上，对于查询操作的优化是显然的（在查找⑥的根节点时，省去了递归长长的子树）

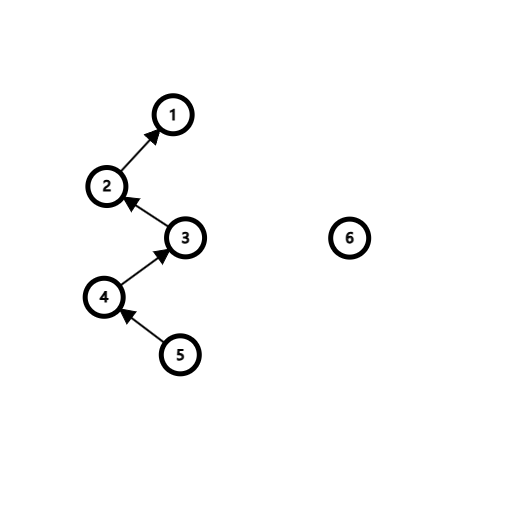
下面给出优化后的合并代码：

int h[N];                        //树的度数组
void init_set(){
    for(int i=1;i<=N;i++){
        fa[i]=i;
        h[i]=0;                  //初始化高度为零
    }
}
void join(int x,int y){
    int f1=find(x),f2=find(y);
    if(h[f1]==h[f2]){
        h[f1]++;                 //合并，树的高度加一
        fa[f2]=f1;
    }
    else{
        if(h[f1]<h[f2]){
            fa[f1]=f2;           //矮树合并到高树上，高树高度不变
        }
        else
            fa[f2]=f1;
    }
}

1.3 查询的优化（路径压缩）

实际上，在并查集的一棵树中，我们只关心其对应的根节点是什么，并不关心其具体形态，这意味着下图中两树是等价的。

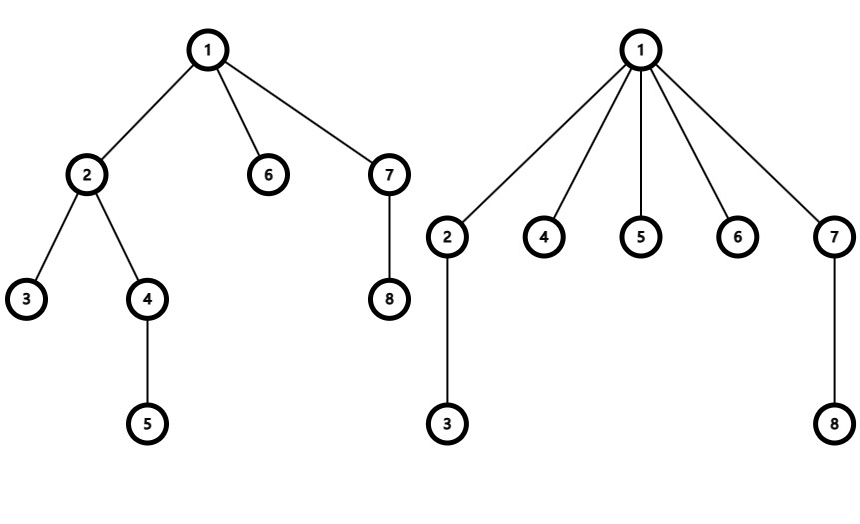
因此，我们可以在每次执行 \(find\) 操作时把访问过的节点（即查询过的祖先元素）都直接指向树根，即把上图中左树变为右树，即为路径压缩优化，以下给出使用路径压缩的查询操作代码：

int x;
int find(int x){
    if(fa[x]==x) return x;
    return fa[x]=find(fa[x]);    //直接指向根节点
}

可以看出，路径压缩优化对并查集的速度优化是巨大的（因为合并操作也需要用到查询操作）其省去了巨量的重复递归，使得均摊复杂度来到了 \(O(\log n)\) 。

在一般题目中，只使用路径压缩优化的并查集就已经可以。

1.4 并查集的极限优化（个人认为）

在使用了路径压缩优化后，树的高度都应为2，那么使用以树的高度为秩的按秩合并便不在可行，于是在此给出秩的第二种定义，即为集合的大小，同时，当秩被定义为集合大小时，“按秩合并”也并被称作“启发式合并”。

此时按秩合并的可行性证明：

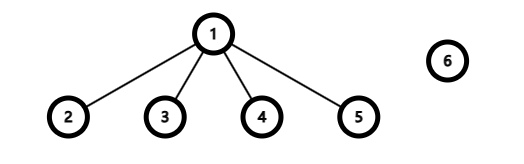
对于上图中的两棵树，我们可以明显看出当把右树（即小树）合并为左树（即大树）的子树时，复杂度更低（因为避免了 \(fa[]\) 的大量修改）。

下面给出模版：

int N,x,m,n;
int fa[maxn],sum[maxn];
void init_set(){
    for(int i=1;i<=maxn){
        fa[i]=i;
        sum[i]=1;
    }
}
int find(int x){
    if(fa[x]==x) return x;
    return fa[x]=find(fa[x]);
}
void join(int x,int y){
    x=find(x),y=find(y);
    if(sum[x]>=sum[y]){
        sum[x]+=sum[y];
        fa[y]=x;
    }
    else{
        fa[x]=y;
        sum[y]+=sum[x];
    }
}

由于前面已经解释过，同理可得，本处不再打注释。

对于此模版来说，复杂度可进一步降低到 \(O(a(N))\) ，其中 \(a(N)\) 可近似为常数。

1.5 “边带权”的并查集

普通的并查集应用中，元素之间只有归属关系，而没有权值。如果在元素之间加上权值，应用将会更广泛。

（1. 带权值的路径压缩优化

只需累加权值 \(d[]\) 即可（具体情况具体分析）。

int d[maxn];
int find(int x){
    if(x!=fa[x]){
        int f1=fa[x];          //记录父节点
        fa[x]=find(fa[x]);     //路径压缩，递归至根节点
        d[x]+=d[f1];           //权值更新为x至根节点的权值
    } 
    return fa[x];
}

（2. 带权值的合并

把 \(x\) 与 \(y\) 进行合并，即在 \(x\) 的根 \(fx\) 与 \(y\) 的根 \(fy\) 之间增加权值即可。

int num;
void join(int x,int y,int num){
    x=find(x),y=find(y);
    if(x!=y){
        fa[x]=y;                  //将x的树作为y的子树
        d[x]=num;                 //在fx与fy之间添加权值
    }
}

为什么不写按秩合并的优化版？因为要留给大家思考的空间 \(OwO\) 。~~好吧，我懒得写， \(QAQ\) 。~~

1.6 拓展域的并查集

对于复杂的并查集问题，单个的并查集无法解决，对于这样的问题，我们一般需要多个并查集互相推出，即将一个子节点拆为多个子节点，运用子节点之间的关系相互推出。

对于其具体实现方法，以下面这个题为例：

P2024 [NOI2001] 食物链

分析，对与本题，我们可以将动物 \(i\) 分为 \(i_{self}\) , \(i_{eat}\) 与 \(i_{enemy}\) 三个子节点，我们定义 \([1,maxn]\) 为 \(self\) 域， \((maxn,2*maxn]\) 为 \(eat\) 域， \((2*maxn,3*maxn]\) 为 \(enemy\) 域，即同时维护三个分别为 \(self\) ， \(eat\) ， \(enemy\) 的并查集，利用并查集之间的关系推出是否是假话。

在处理每句话之前，都要检查其真假性：

有两种信息与“ \(x\) 与 \(y\) 是同类”矛盾：

\(x_{eat}\) 与 \(y_{self}\) 在同一集合（即 \(x\) 吃 \(y\) ）
\(x_{self}\) 与 \(y_{eat}\) 在同一集合（即 \(y\) 吃 \(x\) ）

若与上述任何一条都不矛盾，则：

join(x,y);
join(maxn+x,maxn+y);
join(2*maxn+x,2*maxn+y);   //注意域的范围 !!!

有两种信息与“ \(x\) 吃 \(y\) ”矛盾：

\(x_{self}\) 与 \(y_{self}\) 在同一集合（即 \(x\) 与 \(y\) 是同类）
\(x_{self}\) 与 \(y_{eat}\) 在同一集合（即 \(y\) 吃 \(x\) ）