并查集

• 并查集
  • （1.概念：
  • （2.详解
    • Q1：如何表示不同的家族
    • ans1：
    • Q2：如何将两个人归到同一个家族中
    • ans2：
    • CODE：
    • PS:

（1.概念：

处理 不相交 可合并 的集合关系的数据结构叫做并查集；

（2.详解

例题：P1551 亲戚

一道并查集的板子题

我们来详细解一下：

Q1：如何表示不同的家族

ans1：

即如何表示不同的集合；

再此采用的是选择集合的代表元素；

代表元素不同则所属集合不同；

Q2：如何将两个人归到同一个家族中

ans2：

即如何合并两个集合；

合并两个集合也就简化成了改集合变代表元素的指针的指向；

解释完这两个问题后，我们回到题目：

CODE：

1. 寻找家族族长（集合代表元素）：

   int find(int x)
   {
       if(x==qin[x])                  //qin数组为指针数组，
           return x;
       return qin[x] = find(qin[x]);  //递归找族长，同时更新指针数组指向，后面再说
   }
   

2. 合并家族（合并集合）：

   void join(int c1,int c2)
   {
       int f1=find(c1),f2=find(c2);
       if(f1!=f2)                      //若不在一个家族
           qin[f1] = f2;               //更改c1家族的代表元素即可
   }
   

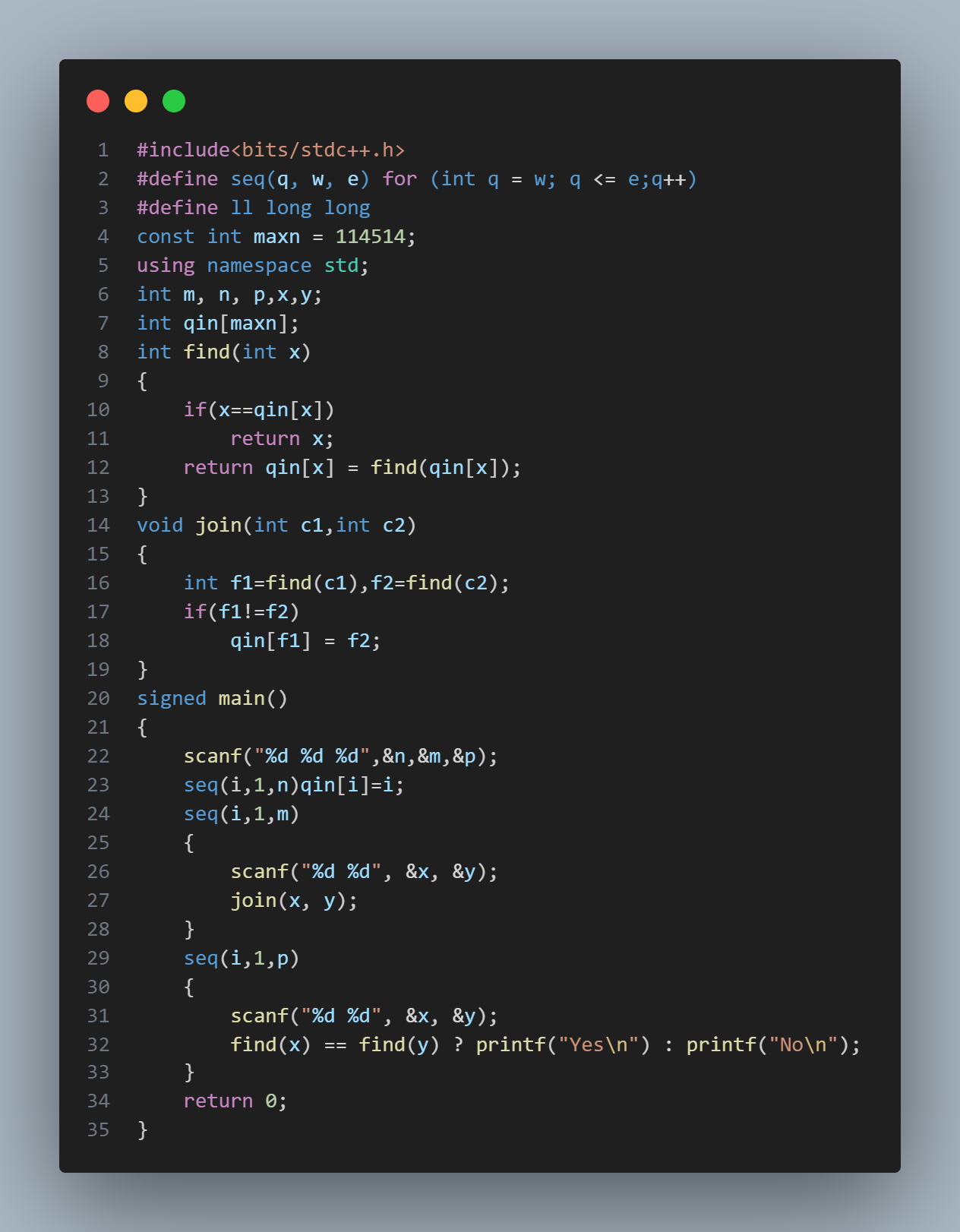
3. 全代码如下：

   

PS:

​ 还有一个问题：在寻找函数中 return qin[x] = find(qin[x]); 的作用

其实也很好理解，这是一种优化，叫做路径压缩优化；

在本题的解答树中，我们可以明显的看出，这种做法可以将每个新加入的成员的指针都指向家族的族长；

而避免了每次查询时都需重复递归，大大降低了时间复杂度；