原文链接:https://blog.csdn.net/dl962454/article/details/102999067 分类专栏: 深度学习 文章标签: LSTM 神经网络
文章目录
1、普通RNN和LSTM
在实际应用中普通的 RNN 是非常难以训练的:
假设有一段关键文字“xxxx[key]xxx…xxxx”要求 RNN 分析出与 key 相关的 结果,即文字中的 key 是 RNN 进行分析所需要的关键数据。但此时 key 出现在 句子开头(t1),此信息源的记忆要经过非常一段长的时间才可以达到最终状态点, 如图
前向传播得到误差,反向传递误差时,每次都会乘一个系数 w,当这个 w 小 于 1 时,每次反向传递都会让 RNN 的误差缩小,经过若干次误差反向传递, 到 key 状态时,误差很近似等于 0 的情况,这就叫梯度消失或者梯度弥散,反 之,如果 w 大于 1,每次反向传递都会让 RNN 的误差变大,经过若干次误差的 反向传递,到 key 的状态时,误差将会是一个非常大的数(无穷大),这种情况 叫做梯度爆炸。这样导致很难确定一个初始值让 RNN 收敛。
假设X0的输入为”我住在深圳”,后面插入了很多其他的句子,然后在X t X_tXt输入了“我在市政府上班”。由于X 0 X_0X0与X t X_tXt相差很远,当RNN输入到Xt时,t时刻的记忆h t h_tht已经丧失了X 0 X_0X0时保存的信息了。因此在X t X_tXt时刻神经网络无法理解到我是在哪一个城市的市政府上班了。
为了解决这个问题 ,提出了 Long short-term memory (简称 LSTM,下 同),比起普通的 RNN,LSTM 引入了三个门的概念:遗忘控制门,输入控制门,输出控制门。遗忘控制门用来确定上一个隐藏层状态的信息哪些是重要的,输入控制门用来确定当前状态的哪些信息是重要的,输出控制门用来确定 下一个隐藏层状态。
LSTM 的 cell 结构图如图:
2、LSTM 原理讲解
在理论上,RNN绝对可以处理这样的长期依赖问题。人们可以仔细挑选参数来解决这类问题中的最初级形式,但在实践中,RNN却不能够成功学习到这些知识。因此,LSTM就是为了解决长期依赖问题而生的,LSTM通过刻意的设计来避免长期依赖问题。记住长期的信息在实践中是 LSTM的默认行为,而非需要付出很大代价才能获得的能力!
LSTM的核心思想就是cell的状态,如图所示,最上方平行的一条线可称为“主线”,贯穿整个链,只进行少量的信息交互,信息流保持不变会很容易。
所有RNN都具有一种重复神经网络模块的链式的形式。在标准的RNN 中,这个重复的模块只有一个非常简单的结构,例如一个tanh层。
先介绍上图中的符号意义:
在上面的图例中,每一条黑线传输着一整个向量,从一个节点的输出到其他节点的输入。粉色的圈代表 pointwise 的操作,诸如向量的和,而黄色的矩阵就是学习到的神经网络层。合在一起的线表示向量的连接,分开的线表示内容被复制,然后分发到不同的位置。如下:
Neural network layer:神经网络层,可以看作一个个的非线性处理模块。
Pointwise operation:逐点运算,逐点运算举个逐点乘法的例子就是:0.5×[1., 2., 3.] = [0.5, 1.0, 1.5]。
Vector transfer:信息传递方向。
Concatenate:这个很好理解,信息的汇合。
Copy:与上面对应,信息的复制。
接下来将对LSTM进行逐步理解。在每个记忆单元(图中A)中包括细胞状态(C t C_tCt),遗忘门,输入门和输出门。这些门结构能让信息选择性通过,用来去除或者增加信息到细胞状态。
3、细胞状态及LSTM的三个控制门
3.1 细胞状态(LSTM关键)
t时刻的记忆信息,用来保存重要信息。就好像我们的笔记本一样,保存了我们以前学过的知识点。如下图的水平线从图上方贯穿运行,直接在整个链上运行,使得信息在上面流传保持不变会很容易。
运作:它记忆的信息就在这条传送带上从后往前传,传送的时候会发生一些信息的交互,信息就在这上面一直保存。我可以在这条传送带上取值,也可以在上面输入值。 C t C_tCt是memory,也就是记忆。
控制:如何控制cell state?我们会通过一个叫‘门’gate的东西来处理它,会给信息进行一个选择性的放行,来去除或者增加信息。先放结论:它包含着什么?包含一个sigmoid+一个pointwise。先看sigmoid,它的输出结果会得出一个概率p,是0-1的一个值。我要做的就是一个信息的变更,到底让不让这部分信息,(前提:我的脑容量就这么大,只能记忆这么多东西,再多我记不住了)让他们接着往下存下去,还是说这部分记忆就没用了就更新了?(这里补充一下,忘记信息之后要更新)肯定要有个东西来控制它,这里我们控制的就是一个sigmoid,描述每个部分有多少量可以通过。这个概率可以和任何一个东西相乘,表示我允许你多大的量可以通过。0表示不需任何量通过,1表示允许任何量通过。
3.2遗忘控制门
遗忘控制门是LSTM工作的第一步,它用来决定我们从上一个细胞状态中丢弃哪些内容。遗忘控制门通过读取h t − 1 h_{t−1}ht−1和x t x_txt,再通过S函数层,得出一个0-1之间的数值(这里不能用阶跃函数作为激活函数,因为它在所有位置的梯度都为0,无法作为激活函数),得出f t f_tft,对应于每个C t − 1 C_{t−1}Ct−1的数字(图中表示为上方主线的输入).其中,1表示“完全保留”,0表示“完全舍弃”,即对向量中的每个值是完全忘记或者完全记住。
在语言模型中,细胞的状态用来预测当前主语的性别,因此,可能选出正确的代词。这时候我们将希望忘记旧的主语.以一个例子来说明遗忘门的作用:在语言模型中,细胞状态可能保存着这样的重要信息:当前主语为单数或者复数等。如当前的主语为“小明”,当输入为“同学们”,此时遗传门就要开始“干活”了,将“小明”遗忘,主语为单数形式遗忘。
遗忘门工作过程: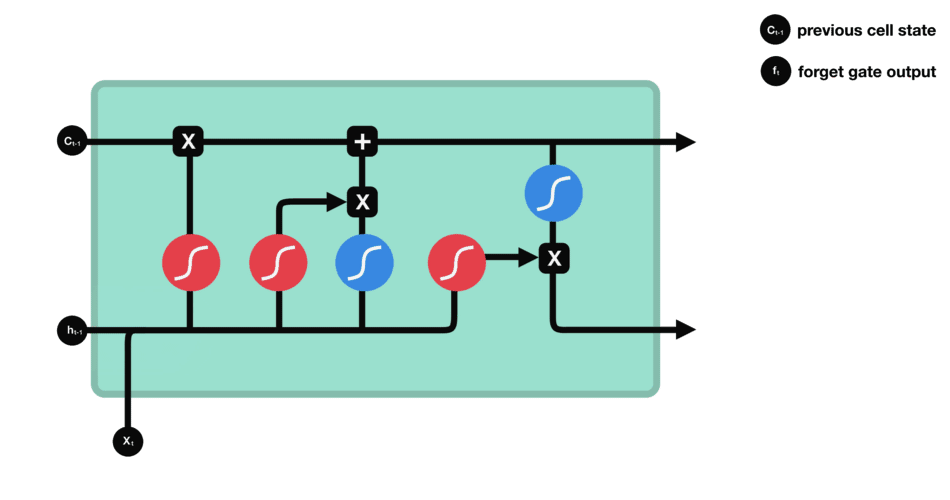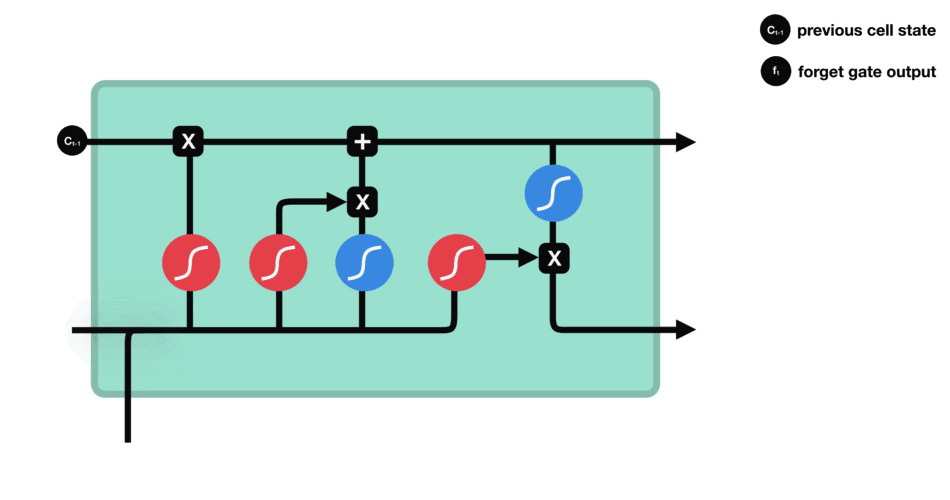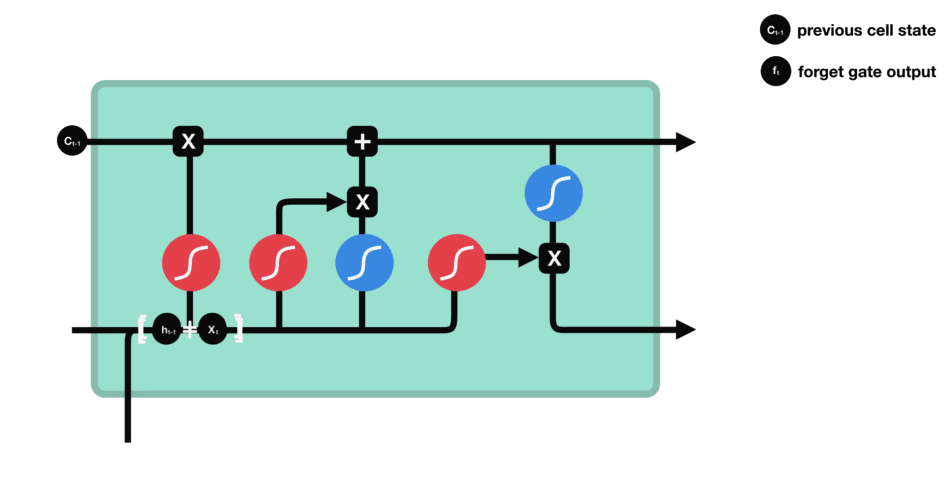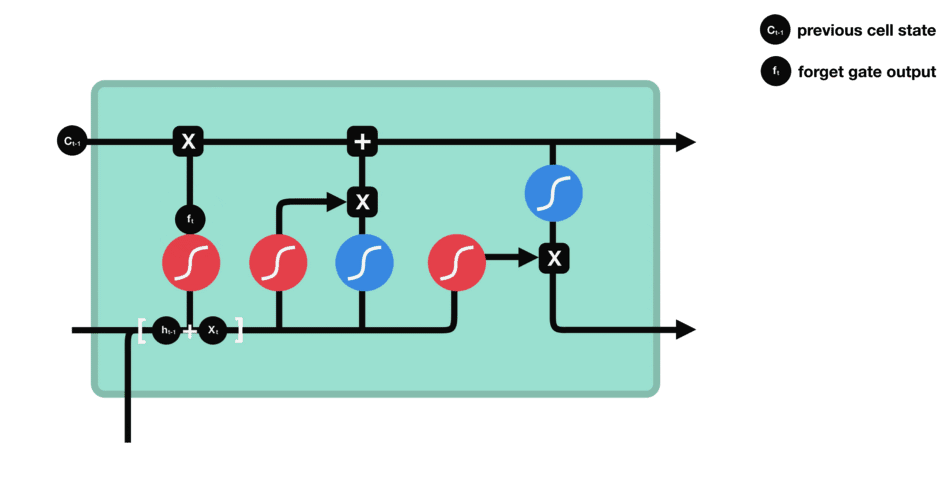
3.3 输入控制门
输入控制门用来更新重要信息,即就是用来确定什么样的新信息需要保留在cell的状态中。
输入控制门分两部分
1、h t − 1 h_{t−1}ht−1和x t x_txt先经过S函数层得到i t i_tit来确定什么样的值是重要的,在通过一个tanh层得到C t ~ \tilde{C_t}Ct~,i t i_tit也是范围0-1的一个概率值p,i t i_tit做的事就是对目前为止学到的所有信息做一个过滤,它的概率值表明,现在学到的哪部分新知识可以更新我之前的记忆的,也就是拿它过滤本次记忆。而本次学到的所有知识就是C t ~ \tilde{C_t}Ct~。要把本次学到的信息,放到之前学到的所有信息中。所以用i t i_tit这个概率,对C t ~ \tilde{C_t}Ct~做一个过滤,补充到之前学习到的信息中。
比如,在语言模型中,我们希望增加新的主语的性别到细胞状态中,来代替需要忘记的主语。
输入门工作过程: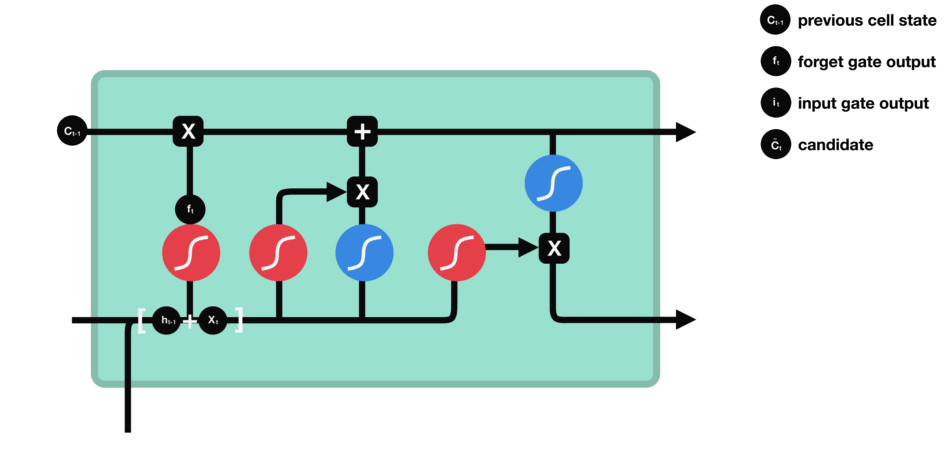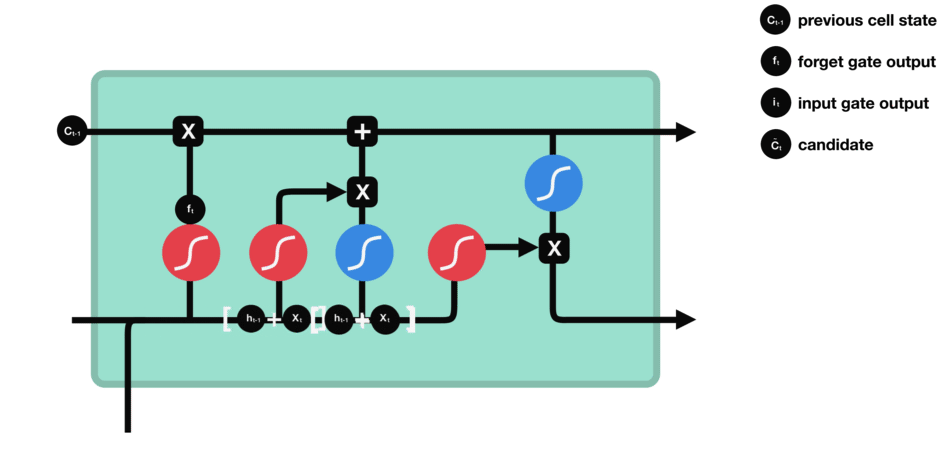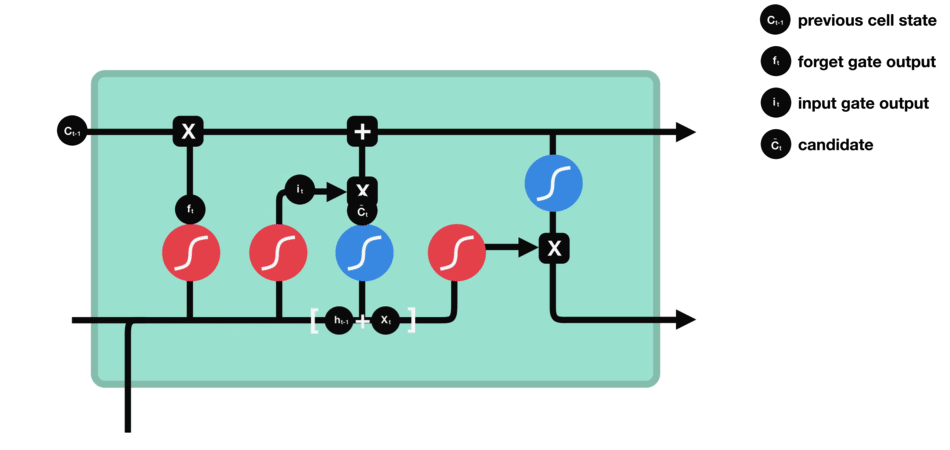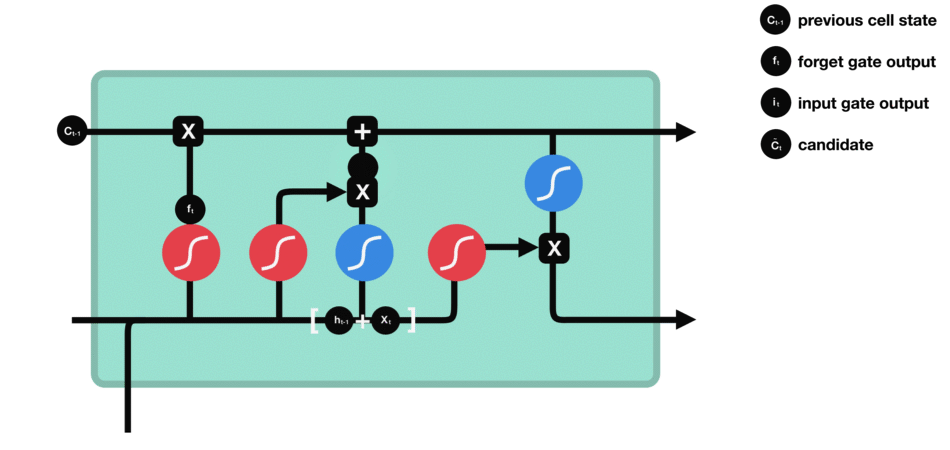
2、更新cell状态C t − 1 C_{t−1}Ct−1 更新为C t C_tCt,更新过程如下
f t ∗ C t − 1 f_t*C_{t-1}ft∗Ct−1就是忘记旧的值,i t ∗ C t ~ i_t *\tilde{C_t}it∗Ct~用来添加新的值。f t f_tft就是旧的记忆的通过率,也就是我们的gate门,i t i_tit是本次信息的过滤器,C t ~ \tilde{C_t}Ct~是本次学习到的知识。
细胞状态更新过程: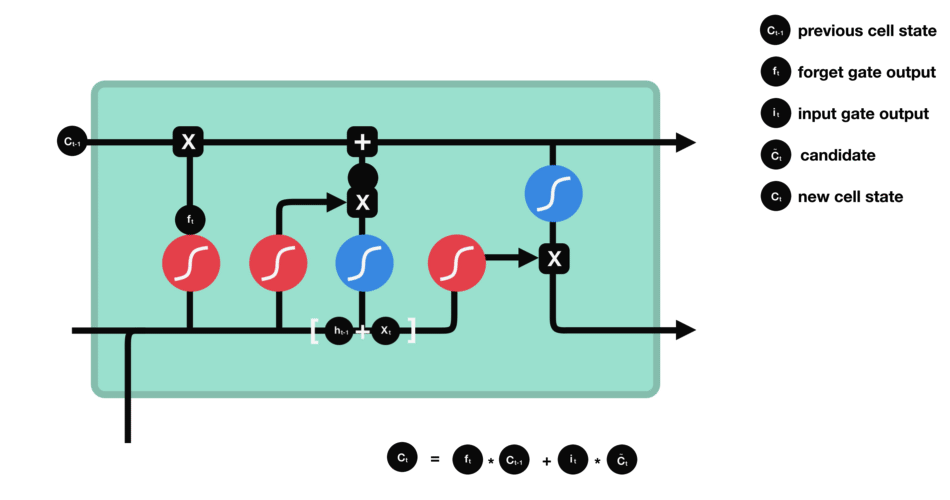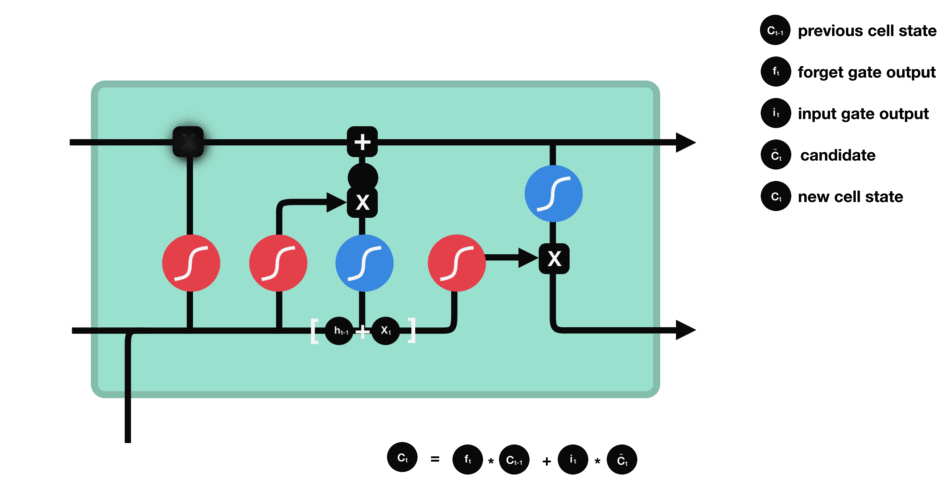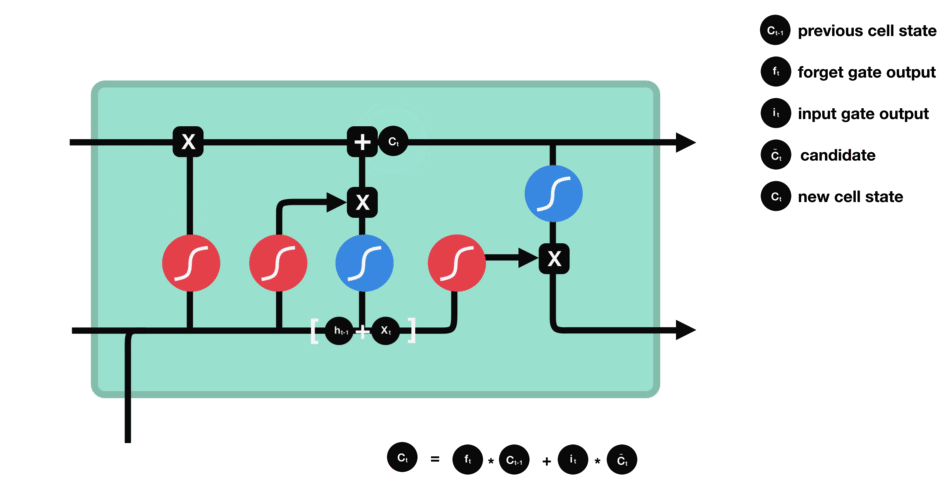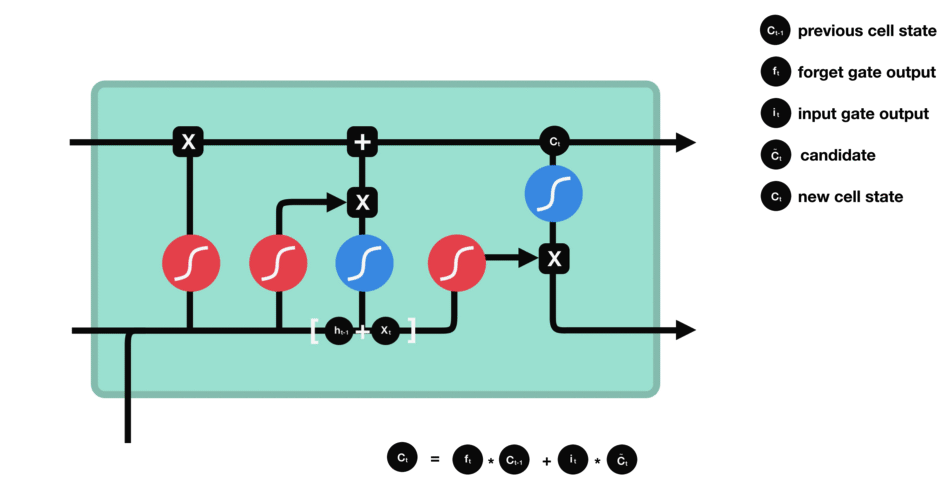
3.4 输出控制门
输出控制们用来确定我们需要输出什么值,输出值基于细胞状态。
我们先将h t − 1 h_{t-1}ht−1和x t x_txt的组合经过Sigmoid函数层,再与C t C_tCt经过tanh层的结果相乘,确定输出部分:
C t C_tCt是我更新以后之前所学到的全部知识,而当我解决当前需解决的问题的时候,只需要某些知识,因此,用一个o t o_tot去筛选,他依然是一个0-1之间的概率,他会从C t C_tCt所有知识中去筛选出来解决当前问题的信息,然后的出结果。
举个例子,同样在语言模型中,细胞状态中此时包含很多重要信息,比如:主语为单数形式,时态为过去时态,主语的性别为男性等,此时输入为一个主语,可能需要输出与动词相关的信息,这个时候只需要输出是单数形式和时态为过程,而不需要输出主语性别就可确定动词词性的变化。
输出门工作过程: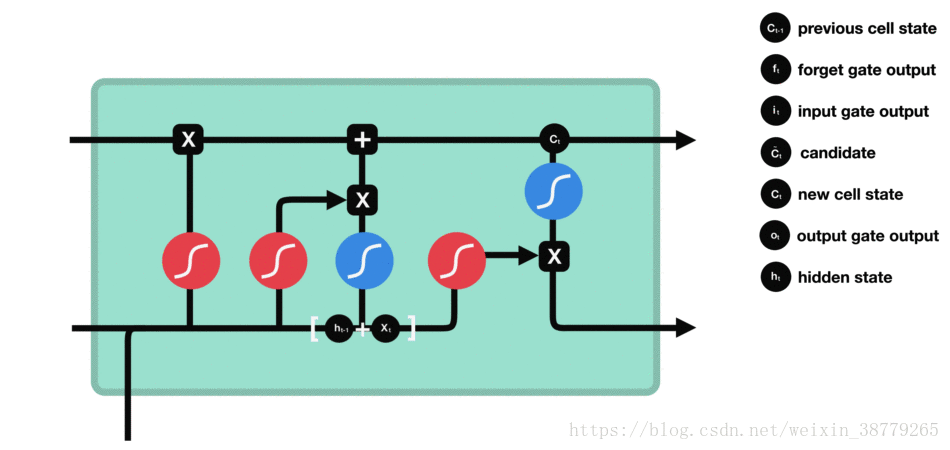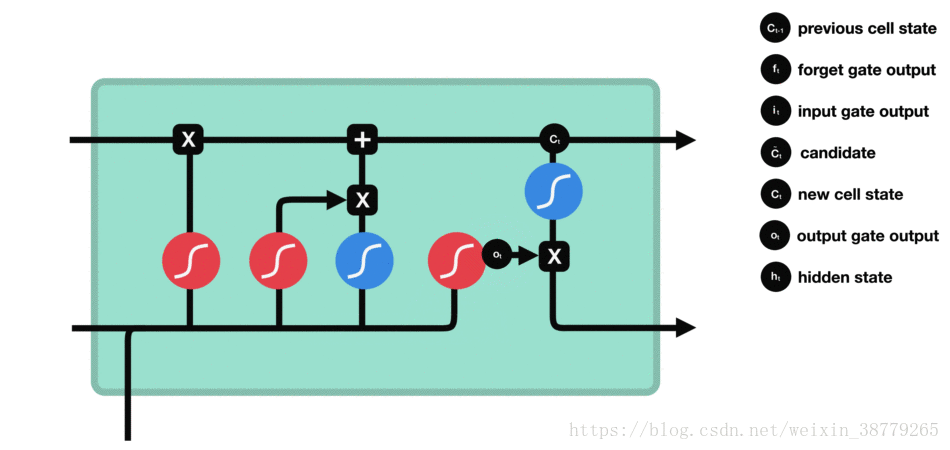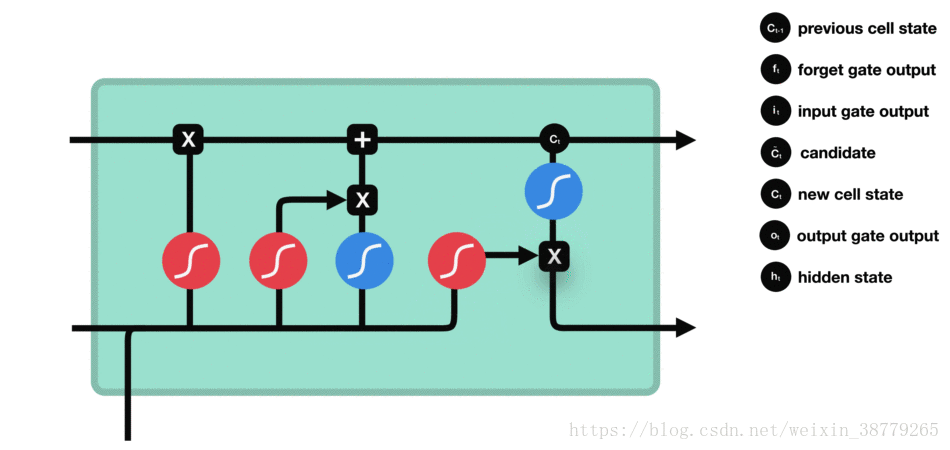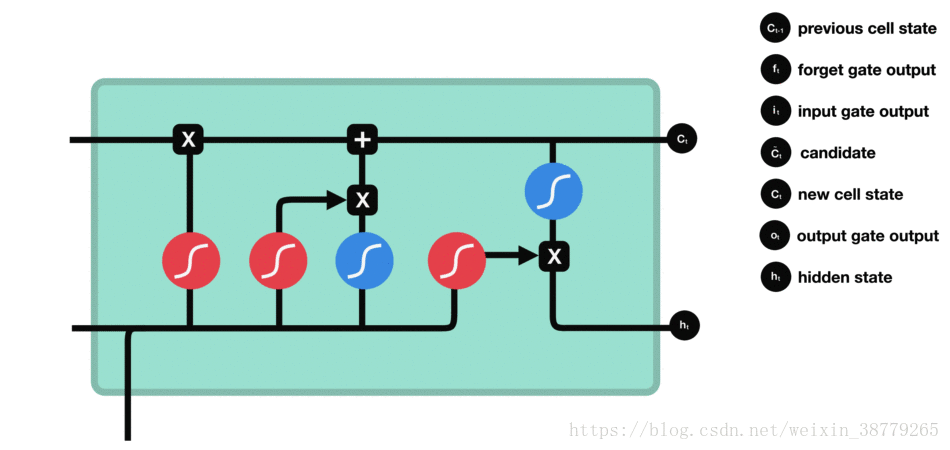
所以整个LSTM的更新和RNN是非常像的。唯一的区别是:我先确定我丢掉什么,我再确定我要添加什么,再把它加上,我再根据最后的记忆来产出结果。总的来说,LSTM用两个门来控制单元状态C的内容,一个是遗忘门(forget gate),它决定了上一时刻的单元状态C t − 1 C_{t-1}Ct−1有多少保留到当前时刻C t C_tCt;另一个是输入门(input gate),它决定了当前时刻网络的输入x t x_txt有多少保存到单元状态C t C_tCt。LSTM用输出门(output gate)来控制单元状态C t C_tCt有多少输出到LSTM的当前输出值h t h_tht。
4、双向LSTM(Bi-directional LSTM)
如上篇文章BRNN所述同理,有些时候预测可能需要由前面若干输入和后面若干输入共同决定,这样会更加准确。因此提出了双向循环神经网络,网络结构如下图。可以看到Forward层和Backward层共同连接着输出层,其中包含了6个共享权值w 1 − w 6 w_1-w_6w1−w6。
在Forward层从1时刻到t时刻正向计算一遍,得到并保存每个时刻向前隐含层的输出。在Backward层沿着时刻t到时刻1反向计算一遍,得到并保存每个时刻向后隐含层的输出。最后在每个时刻结合Forward层和Backward层的相应时刻输出的结果得到最终的输出,用数学表达式如下: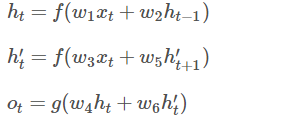
5、GRU(Gated Recurrent Unit)门控循环单元
5.1 GRU概述
GRU是LSTM网络的一种效果很好的变体,它较LSTM网络的结构更加简单,而且效果也很好,因此也是当前非常流形的一种网络。GRU既然是LSTM的变体,因此也是可以解决RNN网络中的长依赖问题。
在LSTM中引入了三个门函数:输入门、遗忘门和输出门来控制输入值、记忆值和输出值。而在GRU模型中只有两个门:分别是更新门和重置门。GRU使用同一个门控z t z_tzt就同时进行遗忘和选择记忆,具体结构如下图所示:
图中的z t z_tzt和r t r_trt分别表示更新门和重置门。更新门用于控制前一时刻的状态信息被带入到当前状态中的程度,更新门的值越大说明前一时刻的状态信息带入越多。重置门控制前一状态有多少信息被写入到当前的候选集 h ~ t \tilde h{_t}h~t 上,重置门越小,前一状态的信息被写入的越少。
5.2 GRU前向传播
根据上面的GRU的模型图,我们来看看网络的前向传播公式:

其中[]表示两个向量相连,*表示矩阵的乘积。
( 1 − z t ) ∗ h t − 1 (1-z_t)*h_{t-1}(1−zt)∗ht−1: 表示对原本的隐藏状态进行选择性的忘记。
z t ∗ h t ~ z_t*\tilde{h_t}zt∗ht~: 表示对包含当前节点信息的h t ~ \tilde{h_t}ht~进行选择性的记忆,这里z t z_tzt也会忘记上一维度h t − 1 h_{t-1}ht−1中的一些不重要的信息。或者,这里我们更应当看作是对h t − 1 h_{t-1}ht−1维度中的某些信息进行选择。
h t = ( 1 − z t ) ∗ h t − 1 + z t ∗ h t ~ h_t=(1-z_t)*h_{t-1}+z_t*\tilde{h_t}ht=(1−zt)∗ht−1+zt∗ht~: 这一步操作就是忘记传递下来的h t − 1 h_{t-1}ht−1中的某些维度信息,并加入当前节点输入的某些维度信息。
可以看到,这里的遗忘( 1 − z t ) (1-z_t)(1−zt)和选择z t z_tzt是联动的。也就是说,对于传递进来的维度信息,我们会进行选择性遗忘,则遗忘了多少权重( 1 − z t ) (1-z_t)(1−zt),我们就会使用包含当前输入的h t ~ \tilde{h_t}ht~中所对应的权重进行弥补z t z_tzt。以保持一种“恒定”状态。
5.3 GRU的训练过程
从前向传播过程中的公式可以看出要学习的参数有W r 、 W z 、 W h 、 W o W_r、W_z、W_h、W_oWr、Wz、Wh、Wo。其中前三个参数都是拼接的(因为后先的向量也是拼接的),所以在训练的过程中需要将他们分割出来:


在算出了对各参数的偏导之后,就可以更新参数,依次迭代直到损失收敛。
概括来说,LSTM和GRU都是通过各种门函数来将重要特征保留下来,这样就保证了在long-term传播的时候也不会丢失。此外GRU相对于LSTM少了一个门函数,因此在参数的数量上也是要少于LSTM的,所以整体上GRU的训练速度要快于LSTM的。不过对于两个网络的好坏还是得看具体的应用场景。
关于GRU更好的文章参考:人人都能看懂的GRU
6、Keras实现LSTM和双向LSTM




7、LSTM里面比较重要的几个问题:
7.1 为什么要使用激活函数?
如果不用激励函数(其实相当于激励函数是f(x) = x),在这种情况下你每一层输出都是上层输入的线性函数,很容易验证,无论你神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果相当,这种情况就是最原始的感知机(Perceptron)了。
正因为上面的原因,我们决定引入非线性函数作为激励函数,这样深层神经网络就有意义了(不再是输入的线性组合,可以逼近任意函数)。最早的想法是sigmoid函数或者tanh函数,输出有界,很容易充当下一层输入(以及一些人的生物解释balabala)。激活函数的作用是为了增加神经网络模型的非线性。否则你想想,没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。所以你没有非线性结构的话,根本就算不上什么神经网络。
关于激活函数可以参见这篇文章,讲解的非常详细神经网络激活函数的作用是什么?
7.2 为什么用sigmoid,为什么不用relu?为什么不用tanh?
Sigmoid会饱和,确实,可能会带来问题。注意看公式,0-1才可以起到筛选的作用,如果用relu信息就会全过去了,信息它可能会爆炸,每层都会变大,下一层更大,就做不到把每层的信息都压缩到一个共同的范围了。

Relu是做不到的,它大于0的就全过去了,信息会越来越多。
用tanh的话,它双曲正切你想一下图像,它可能会出现一个负值,如-0.2,或者-0.5之类的,就会否定掉之前的全部的。
总结来说:激活函数求导,大于1或小于1,累乘的过程数值会不断变大或变小,出现梯度爆炸或梯度消失的问题。而relu求导梯度永远等于1,所以不会给信息造成影响。
7.3 为什么LSTM比RNN更能解决长时依赖?
RNN怎么修改S t S_tSt的? S t = t a n h ( W X t + U S t − 1 ) S_t=tanh(WX_t+US_{t-1})St=tanh(WXt+USt−1)这是个复合函数,复合函数求偏导是连乘的形式,我用的是双曲正切,双曲正切在x偏大和偏小的时候斜率是接近于0的,所以接近于0会让反向传播的时候,S t S_tSt约等于0,RNN什么都学不到了,因为没有梯度传回来了,也就是没有梯度来校正参数W WW了。
而什么时候会出现 ≈ 0 \approx{0}≈0呢,就是链路非常长的时候,就可能带来梯度消失,也就是梯度弥散。这个时候求导的链式法则是让无数东西的梯度相乘,当有一个 ≈ 0 \approx{0}≈0 时,整个式子的结果就会 ≈ 0 \approx{0}≈0,当我的链路越长时,越有可能出现 ≈ 0 \approx{0}≈0 的情况。
看LSTM,LSTM不是复合函数,是两个函数求和,f(x)+g(x)求偏导的话,得到的是两个偏导的和,即使有一个 ≈ 0 \approx{0}≈0,它不会导致整体约等于0。所以我的梯度往回传的时候是沿着两条轴往回传的。梯度不是顺着一条轴往回传的,LSTM最大的变化就是把RNN的连乘变成了求和,因此,不再会严重地出现梯度消失问题,这意味着即使时间再远,我应该也是学得到的。
以上的公式都不是必须只能这样,有很多变种(基本上没差异),但这篇总结写的是标准的那一种。
LSTM有很多很多的变种,举一个例子,有人会想,我去推断我要以多大程度去计算我要忘记什么东西,为什么只用上一次的输出,为什么不用之前的记忆C t − 1 C_{t-1}Ct−1?其实就有这样的变种,可以把记忆的信息也拿进来和权重相乘。这是已经存在的一个变种了。(这里注意一个地方,向量拼接了以后,如果已存在一个1×100的向量,如果拼了3个这样的向量,它就是一个3×100的向量了,所以在运算的时候W的维度是需要改的)。RNN做损失函数的时候不用每个时间轴的损失都加起来,只求最后一个位置的损失就可以了。Google的大佬大概尝试了上万种RNN架构,发现并非所有任务上LSTM都表现得最好,所以它的变种不是拿一个就能随便用的。
这篇文章可能有些书面了,下面这篇文章比较通俗易懂,奉上地址:
易于理解的一些时序相关的操作(LSTM)和注意力机制(Attention Model)
原文地址:
1、https://colah.github.io/posts/2015-08-Understanding-LSTMs/
2、https://blog.csdn.net/fendouaini/article/details/80198994
3、https://www.cnblogs.com/jiangxinyang/p/9376021.html
下篇文章:注意力机制的基本思想和实现原理(很详细)
最后给出三个学习链接:
1、Softmax 函数的特点和作用是什么?
2、word2vec原理(二) 基于Hierarchical Softmax的模型
3、人人都能看懂的LSTM