标签：状态 chapter9 int visit next 搜索 myQueue

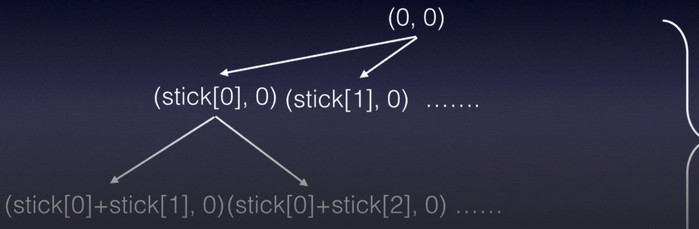
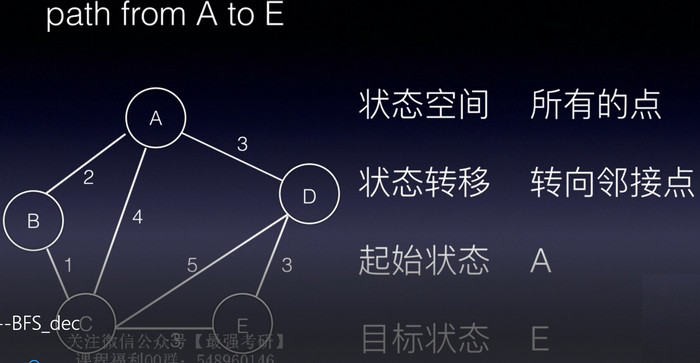
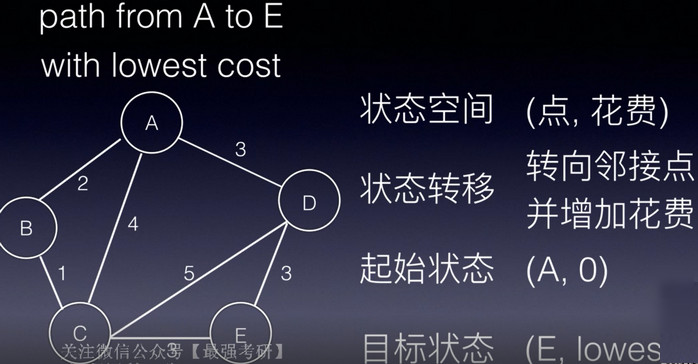
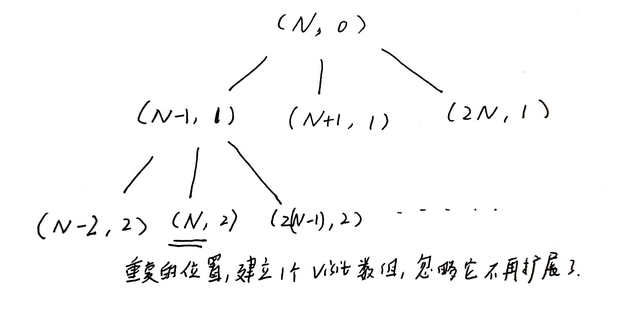
搜索是一种有目的地枚举问题的解空间中部分或全部情况，进而找到解的方法。它的定义是：

起始状态经过一系列的状态转移抵达目标状态，我们一般用搜索树(Search Tree)来表示状态转移

搜索一般包括4个部分：

1、状态空间，也叫解空间；
2、状态转移；
3、起始状态；
4、目标状态。

如何构思上面的四个部分呢，比如状态空间是什么，举个例子：
搜索举例1.jpg

搜索举例2.jpg

1.Search Trees

以寻找从点A到点E的路径问题为例，建立一颗搜索树，建好搜索树之后，还需要确定搜索策略，即先扩展树中的哪个结点，搜索策略有宽度优先搜索、深度优先搜索两种。

搜索树.jpg

2.BFS

策略：每次优先处理当前所有未处理状态中深度最浅的一个状态，即处理最浅的结点。

采用这样的搜索策略，可以发现是一层一层从左到右的扩展，也就是先扩展的先处理，符合队列先进先出特性。

2.1 Catch That Cow

题目描述：
Farmer John has been. informed of the location of a fugitive cow and wants to catch her immediately.He starts at a point N(0≤N≤100000) on a number line and the cow is at a point K (0≤K≤100000)on the same number line. Farmer John has two modes of transportation: walking and teleporting.

Walking:Farmer John can move from any point X to the pointsX- 1 orX+ 1 in a single minute.Teleporting: Farmer John can move from any point xto the point 2X in a single minute.

输入：
Line 1: Two space-separated integers: N and K.

输出：
Line 1: The least amount of time, in minutes, it takes for Farmer John to catch the fugitive cow.

搜索类题目，首先写出搜索问题的4个部分：

1、状态空间 (位置n, 时间t)
2、状态转移 (n-1, t+1), (n+1, t+1), (2n, t+1)，共3种移动方式
3、起始状态 (N, 0)
4、目标状态 (K, lowestTime)

然后建立一颗搜索树：
搜索树抓牛.jpg

确定搜索策略：抓到牛并且花费时间最少，BFS逐层搜索符合题目要求。同时注意到，对重复位置的状态，为了提高搜索的效率，设置visit数组，不再对它进行扩展。

抓住那只牛

//2024-03-08 搜索 Catch that cow
#include <iostream>
#include <cstdio>
#include <queue>

using namespace std;

const int MAXN = 1e5 + 10;
bool visit[MAXN];

struct Status {
    int position;
    int time;
    Status(){}
    Status(int p, int t): position(p), time(t) {}
};

int BFS(int n, int k) {
    queue<Status> myQueue;
    myQueue.push(Status(n, 0));//把搜索树的根结点压入队列
    visit[n] = true;
    while(!myQueue.empty()) { //逐层扩展状态
        Status current = myQueue.front();
        if(current.position == k) {
            return current.time;
        }
        myQueue.pop();
        for(int i = 0; i < 3; ++i) {
            Status next = current;
            if(0 == i) {
                next.position -= 1;
            } else if(1 == i) {
                next.position += 1;
            } else {
                next.position *= 2;
            }
            next.time += 1;
            if(next.position < 0 || next.position > MAXN || visit[next.position]) {
                continue;
            }
            myQueue.push(next);
            visit[next.position] = true;
        }
    }
    return -1;
}

int main()
{
    int n, k;
    while(cin >> n >> k) {
        fill(visit, visit + MAXN, false);
        printf("%d\n",BFS(n, k));
        
    }
    return 0;
}

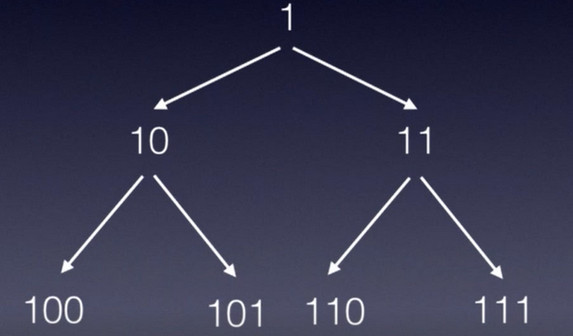
2.2 Find The Multiple

为了缩小状态空间，提高搜索效率，我们转换思路，搜索由0、1组成的数字中，能否被给定的数n整除
首先，写出搜索的4个部分

1、状态空间 0，1构成的数字number
2、状体转移 (number * 10)，(number * 10 + 1)
3、初始状态 1
4、目标状态 number % n == 0

然后建立一颗搜索树：
倍数搜索树.jpg

Find the Multiple

//2024-03-12 Find the Mutiple 自写
#include <iostream>
#include <cstdio>
#include <queue>

using namespace std;

void BFS(int n) {
    queue<long long> myQueue;
    myQueue.push(1);
    while(!myQueue.empty()) {
        long long current = myQueue.front();
        myQueue.pop();
        if(current % n == 0) {
            cout << current << endl;
            return;
        }
        myQueue.push(current * 10);
        myQueue.push(current * 10 + 1);
    }
}

int main()
{
    int n;
    while(cin >> n) {
        if(n == 0)
            break;
        BFS(n);
    }
    return 0;
}

宽度优先搜索常被用来求解最优值问题，因为其搜索到的状态总是按照其某个关键字递增。因此，一旦问题中出现最少、最短、、最优等关键字，就要考虑是否是宽度优先搜索问题。

由于深度优先搜索并没有先入先出的特点，所以搜索到需要的状态时，该状态不再像是宽度优先搜索中的状态一样，具有某种最优的特性。因此，使用深度优先搜索策略时，常常是为了知道问题是否有解。

3.DFS

策略：优先处理最深的结点，可以发现先扩展的状态可能较后才处理，与栈的后入先出特性相符，但在实际操作中，往往使用递归的方式来实现DFS。

3.1 A Knight's Journey

像象棋一样，马这个棋字的行走规则是“日”字。
马走日.jpg

同样首先分析搜索问题的4个组成部分：

1、状态空间：当前游历到的点的坐标，以及总共走了多少格 (x, y, step)
2、状态转移：一共8种 (x-1, y-2, step+1)、(x+1, y-2, step+1)...
3、起始状态： (0, 0, 1) 如果存在解，一定是从A1开始搜索，使得游历的字典序最小
4、目标状态： (x, y, sizeof board) 在哪点终止不确定，但格子数确定

画出搜索树：
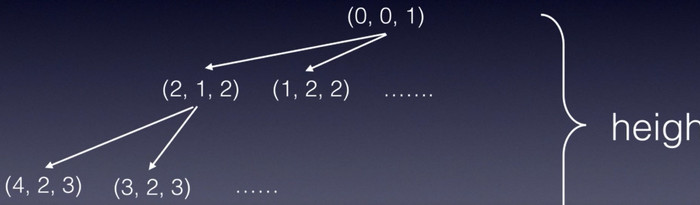
骑士搜索树.jpg

题目要求是找到一条路径能够遍历到棋盘的每一格，相当于要求搜索树的深度height与格子数量相同，并且注意要设置visit数组，之前已经访问过的格子不能再进行扩展或计入树高。

骑士的环球旅行

//2024-03-13 骑士的旅行
#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

int direction[8][2] = {
    {-1, -2}, {1, -2}, {-2, -1}, {2, -1}, {-2, 1}, {2, 1}, {-1, 2}, {1, 2}
};

const int MAXN = 30; //棋盘格数+5安全冗余

bool visit[MAXN][MAXN];

bool DFS(int x, int y, int step, string answer, int p, int q) {
    if(step == p * q) {
        cout << answer << endl << endl;
        return true;
    }
    //步数没到棋盘尺寸，就要进行扩展，有8种扩展方式
    for(int i = 0; i < 8; ++i) {
        int nx = x + direction[i][0];
        int ny = y + direction[i][1];
        if(nx < 0 || nx >= p || ny < 0 || ny >= q || visit[nx][ny]) {
            continue;
        }
        visit[nx][ny] = true;
        char col = ny + 'A';
        char row = nx + '1';
        if(DFS(nx, ny, step + 1, answer + col + row, p, q)) {
            return true;
        }
        visit[nx][ny] = false; //不再访问这个状态，这个状态下的所有扩展状态均无解
    }
    return false;
}

int main()
{
    int n;
    scanf("%d", &n);
    int caseNumber = 0;
    while(n--) {
        int p, q;
        cin >> p >> q;
        memset(visit, false, sizeof(visit));
        cout << "Scenario #" << ++caseNumber << ":" << endl;
        visit[0][0] = true;
        if(DFS(0, 0, 1, "A1", p, q)) {//压入初始状态进行处理
            continue;
        } else {
            cout << "impossible" << endl << endl;
        }
    }
    return 0;
}

3.2 Square

给出若干根长度不一的木棍，问它们能否拼成一个正方形，涉及搜索树减枝，这个例子先留个坑。

首先看搜索问题的4个部分：

1、状态空间： (sum, number) sum指当前已拼凑木棍的长度，第二个number，指已经拼凑成为正方形边长的个数
2、状态转移： (sum + stick[i], number)，有可能发现状态变异-> (0, number + 1)
3、初始状态： (0, 0)
4、目标状态： (0, 4)

画出搜索树，由于扩展的状态数目由木棍数目决定，所以不定：

每往下搜索一层，就多用掉一根木根，所以可以判定木棍是否用完，以及最终拼凑出的边长个数是否等于4，所以应该用DFS搜索策略。
拼成正方形.jpg

因为每个木棍只能使用一次，故要一个visit数组记录是否使用过这根木棍。

留个坑，DFS啊~

标签：状态,chapter9,int,visit,next,搜索,myQueue
From： https://www.cnblogs.com/paopaotangzu/p/18064111

chapter9-搜索