线性规划模型

某机床厂生产甲、乙两种机床，每台销售后的利润分别为4千元与3千元。

生产甲机床需用A、B机器加工，加工时间分别为每台2 小时和1 小时；生产乙机床需用A、B、C三种机器加工，加工时间为每台各一小时。若每天可用于加工的机器时数分别为A 机器10 小时、B 机器8 小时和C 机器7 小时，问该厂应生产甲、乙机床各几台，才能使总利润最大？

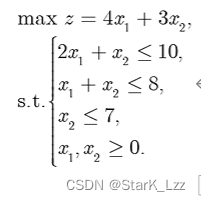
\(s.t.\)为约束条件，$max $ $ z $为目标函数 , \(x_1\) , \(x_2\)为决策变量。

（经典例题）

2. 求解线性规划的MATLAB解法

2.1 基于MATLAB求解器的解法

先将问题化成标准化模型

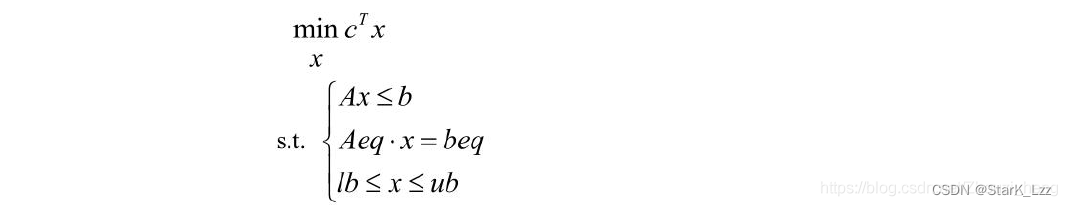
其中c和x为n维列向量!!!，A、Aeq为适当维数的矩阵，b、beq 为适当维数的列向量。【注意：MATLAB 是求的是最小值，不等式的不等号是 ≤ 】

用 linprog 命令( line program)求解线性规划问题 x返回值是决策向量取值，fval 返回值是目标函数最优值 【命令中的空项目用[ ]代替即可】

（不一定存在等式约束和的上下界，如下三种命令，若只有一个边界，另一个可以直接空着）

PS : 命令是求最小值，可以把c矩阵的元素直接加个负号，即求最大值；

[x,fval] = linprog(c,A,b)
[x,fval] = linprog(c,A,b,Aeq,beq)
[x,fval] = linprog(c,A,b,Aeq,beq,lb,ub)

2.2 基于问题的解法

开头例题的程序示例

clear;clc;
c = [-4,-3];
a = [2,1;1,1;0,1];b = [10,8,7];
[x,y]=linprog(c,a,b,[0,0],0,zeros(2,1));
x,y = -y

应用

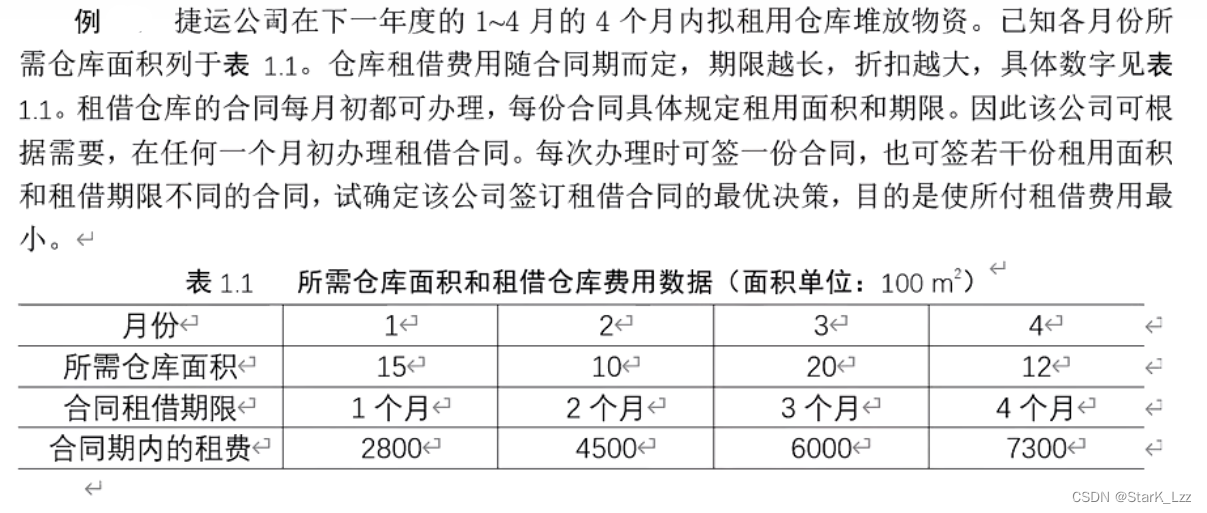
设\(x_{ij}\)为第i个月份租借期限为j的仓库面积，因为5月份不租仓库，所以$ x_{24},x_{33},x_{34},x_{42},x_{43},x_{44}=0 $,可建立如下模型：

解得最优解为：\(x_{11}=3,x_{14}=12,x_{31}=8\)

目标函数最优值是 \(118400\)

3.运输问题（产销平衡）

应用举例

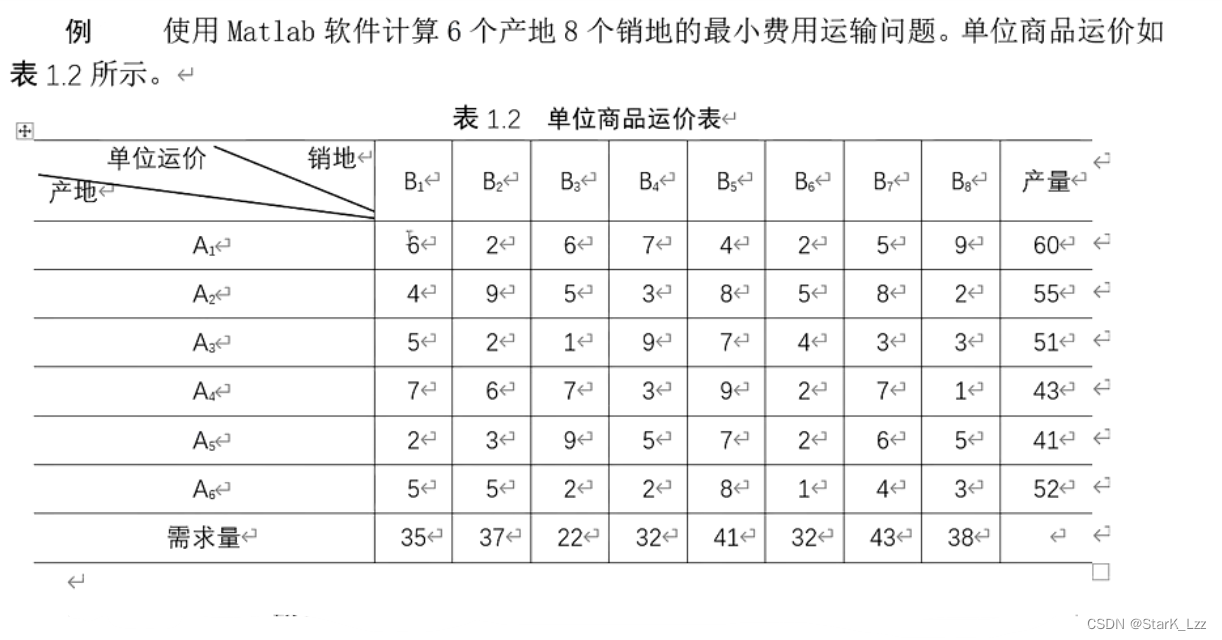
设\(x_{ij}\)表示从产地\(A_i\)运到到销售地\(B_j\)的量，\(c_{ij}\)表示产地\(A_i\)运到到销售地\(B_j\)的运价，\(d_{ij}\)表示销售地\(B_{j}\)的需求量，\(c_{i}\)表示产地的产量。

则目标函数就是使总的运费最小，约束条件有，销售地需求量等于运送量；运送量小于等于产地产量。

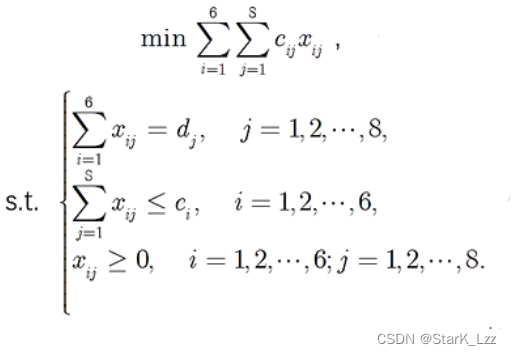
我们用基于问题的方法求解这个线性规划，得\(x_{12}=19,x_{15}=41,x_{21}=1,x_{24}=40,x_{32}=11,x_{37}=40,x_{46}=5,x_{48}=38,x_{51}=34,x_{52}=7,x_{63}=22,x_{66}=27\)

4.问题记录

模型建立方面：
1.模型要注意灵敏度分析，即分析哪个变量的轻微波动对结果的影响更大（现实生活中难免决策变量会发生变化）
2.投资偏好系数：投资者在权衡资产风险和预期收益两方面时，希望选择一个令自己满意的投资组合，因此对风险和收益分别赋予权重，s称为投资偏好系数
记风险为\(P\)，收益为\(Q\)，则需要寻找一个\(s\)，使得\(minP−Q\) ,或 \(max Q−P\)。