分块思想

介绍

分块是一种思想，而不是一种数据结构。

思想就是，将一块大的区间，转换成小的区间来处理。例如，在一个 \(n\) 长度上的数轴，我们可以将其分成 \(\sqrt n\) 个长度为 \(\sqrt n\) 的块来解决。

典型问题

对于一类很典型的问题，可以用分块来做。

• 单点修改，区间查询

这玩意咋做？

线段树来搞 \(O(q \log n)\)，没错，分块他也可以！但是 \(O(q \sqrt n)\)。

我们先与处理一下，把每一个点分到一个他所属的块编号 \(id_i\)。

我们实时维护着两个数组，\(a\) 和 \(b\)，\(a\) 代表的是每一个单独的点它的数值，\(b\) 代表块 \(i\) 它的值（总和）。

• 对于单点修改
  这个操作，我们先把单独点的值修改，\(a_i + x\)。它对应的块也要加对应的值。\(O(1)\)。

• 对于区间查询操作
  我们要找查询中每一个完整的块，然后将其累加起来，然后再暴力找完整块之外的散块 ，加起来，那么时间复杂度也是 \(O(\sqrt n)\)。因为块的长度最多是 $ \sqrt n$，最多只有 $ \sqrt n$ 个块，散块最多 \(2 \times \sqrt n\)。

单点查询也不用说，区间修改的话，也是类似区间查，直接处理一下整块的信息，然后再处理散块的信息，最后，就是一个 $ \sqrt n$ 的时间复杂度。

具体散块和整块的一些细节就不多说，大概就是那样。主要是这种思想。

例题

洛谷P3203

对于这玩意我们可以分块。很容易发现，如果只修改这个点，那么受影响的最多也就是他的这个块，那么我们就直接模拟这个块内，重新跳，如果已经跳到了其他块，那么我们就不用管了，我们直接接着其他块的值，往前即可。然后暴力的把他求出来。所以时间复杂度是 \(O(q \sqrt n)\)。比较抽象（巧妙）的一题，就是运用了分块的思想。巧妙地将暴力转换成了根号级别。与根号分治有异曲同工之妙。

int id[N];//块编号
int l[N],r[N];//块的左端点右端点
int n,q,a[N];
int p[N],s[N];
void sol(int x,int y){
    for(int i = y;i >= x;i--){
        if(a[i] + i > r[id[i]]) p[i]=i+a[i],s[i]=1;//跳到了块外
        else p[i]=p[i+a[i]],s[i]=s[i+a[i]] + 1;
    }
}
void init(){
    int klen = sqrt(n);//块长
    for(int i=1;i <=n;i++) id[i] = (i-1)/klen + 1;
    for(int i=1;i <= id[n];i++) l[i] = (i-1)*klen + 1,r[i] = i*klen;
    r[id[n]] = n;//最右边特判，防止越界了
    sol(1,n);//处理一下 1-n （可以理解为更新
}
int query(int x){
    int ans=0;while(x <= n) ans += s[x],x=p[x];
    return ans;
}
void solve(){
    cin>>n;for(int i = 1;i <= n;i++)cin>>a[i];
    init();cin>>q;
    while(q--){
        int op;cin>>op;
        if(op==1){int x;cin >>x;x++;cout<<query(x)<<endl;}
        else{int x,y;cin>>x>>y;x++;a[x]=y;sol(l[id[x]],r[id[x]]);}
    }
}

莫队介绍

莫队是一个离线算法 + 暴力 + 分块，他可以处理区间内的一些操作。然后他会将每一个查询离线下来，保证，这些查询中都只有查询，没有修改。如果有修改，那么就得要上带修莫队。

普通莫队

我们认为的板子题 ：洛谷 P2709

接下来，我们就要讲的是莫队算法的过程，要点。

对于每一个区间 \([l,r]\)，他都可以在 \(O(1)\) 时间复杂度内从 \([l,r+1]\)，\([l,r-1]\)，\([l-1,r]\)，\([l+1,r]\)。我们可以将 \(l\) 和 \(r\) 看作 xy 轴，画在一个平面图上，例如，看下图：

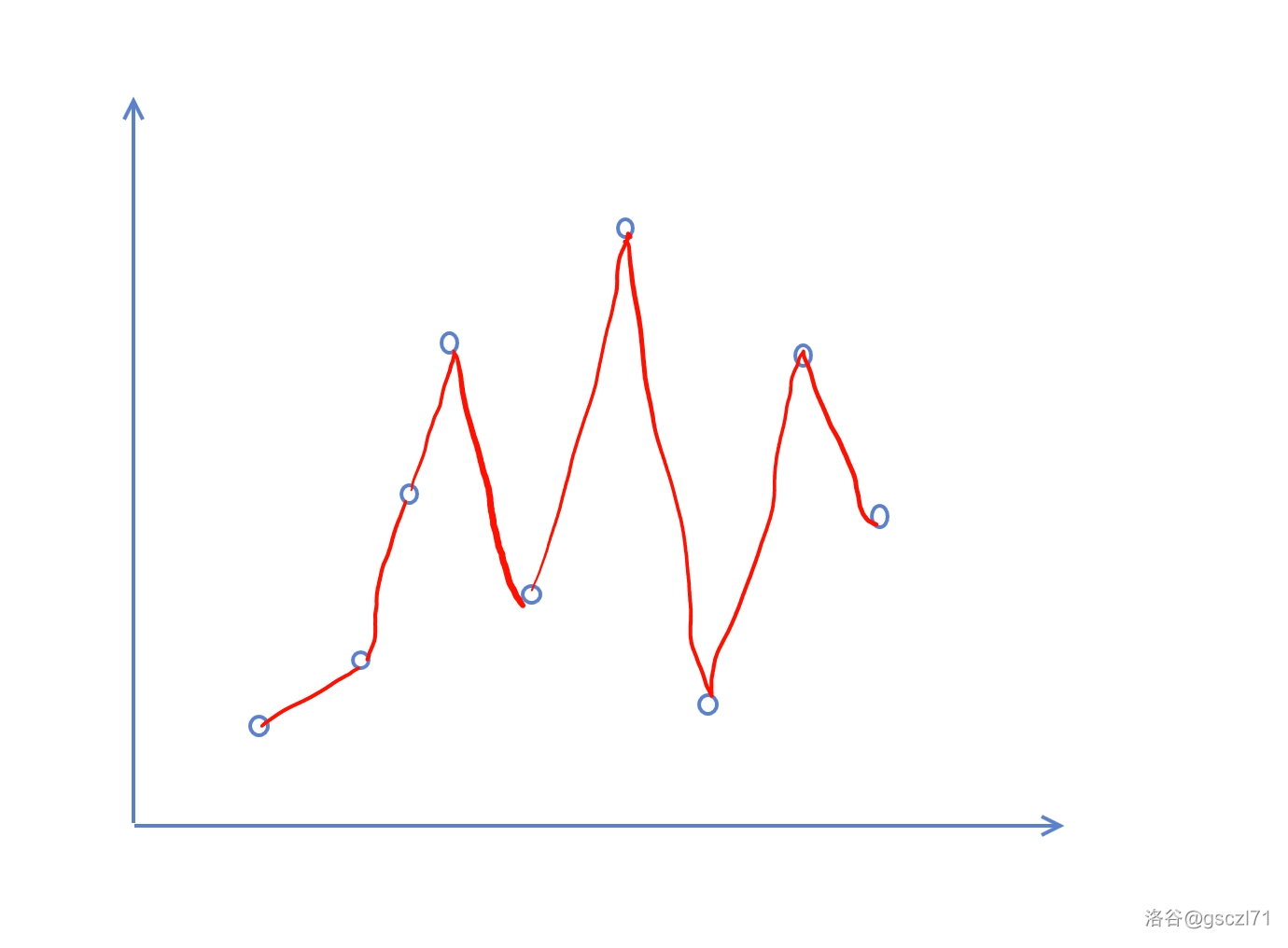
图中每一个圆的点都是一个询问，而这些询问所代表的就是 \(l\) 和 \(r\) 映射在图上的点。那么，红色的线条，就是每两个询问之间所要花的步数，你可以理解为时间复杂度。

对于这上面的点，是询问初始的顺序。我们可以考虑将他最小化吗？可以是可以，但是，这是旅行商问题，自行百度，这玩意只能用状压去搞，你要遍历所有的点，然后最短路，显然还是一个非常困难的问题。

那么，既然我们没办法保证x y轴完全最小化，我们是不是可以保证一个轴最小化，就是一个轴有序递增，这时候用分块，在一个块内，y轴是递增的，x轴随便。这样，我们就会得到下图：

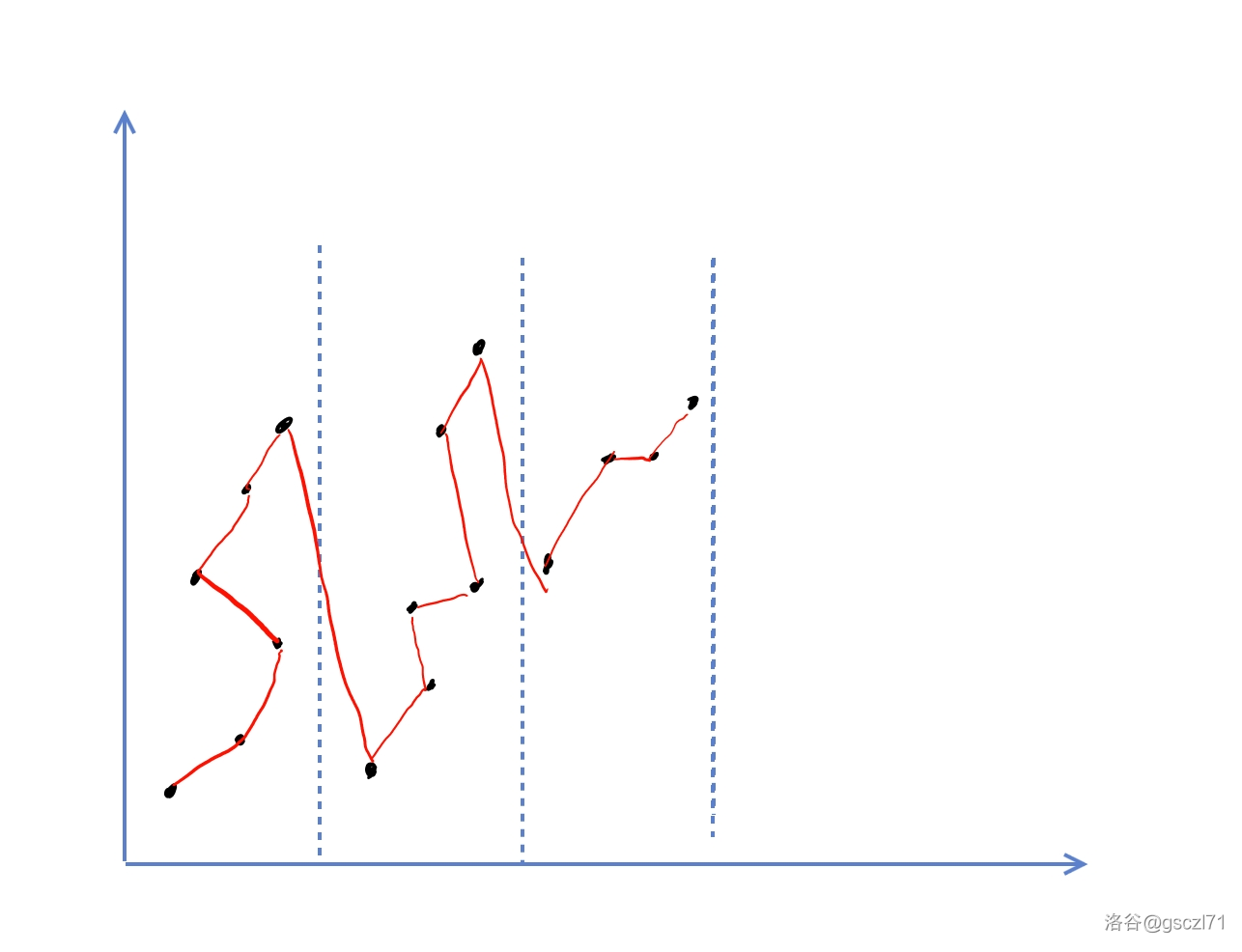
这样，我们在一个块内，就会代价很小，但是，块与块之间的代价却有点大，最多可以卡到 \(n\)。

于是，推出了 奇偶优化，如何奇偶优化呢？就是，分奇偶，就搞出来这个是递增，下一个是递减，这样，就有效程度上减少了这些代价，图变成了这样：

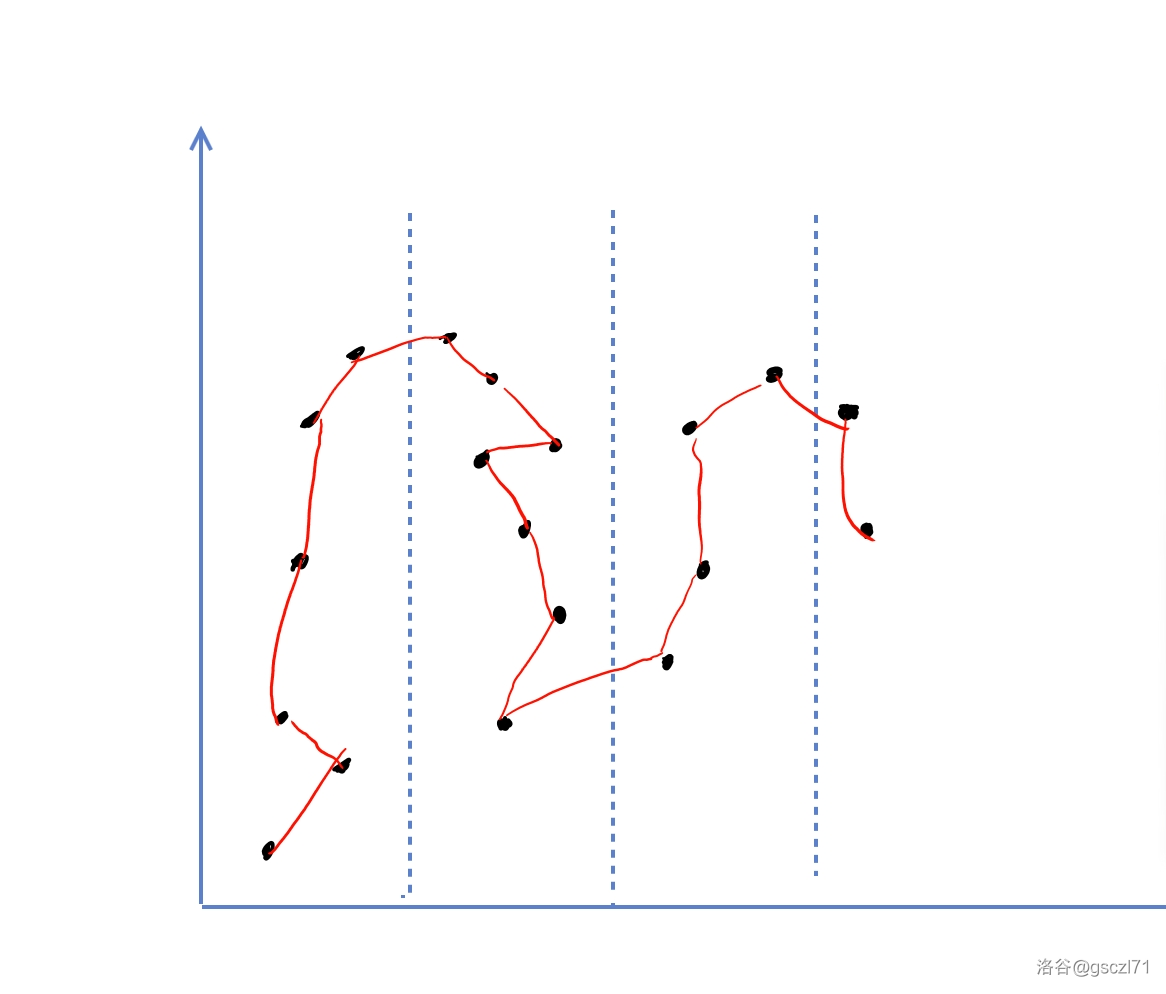
现在，来分析一下时间复杂度。

我们为什么要分块？因为我们学了分块。如果不分块，只对一个维度排序，会怎样？可以想象，这样，我们就会有可能另一个维度一下 -inf，一下inf ，这样，直接卡飞。如果说 \(l\)，\(r\) 都是在 \(n\) 范围内，那么显然，这样的时间复杂度卡成 \(O(n^2)\)。那如果分块了呢？（先不考虑奇偶优化）。一个块内，排序坐标最多 \(O(n)\)，非排序坐标 \(O(\sqrt n)\) 个，每一个 \(O(\sqrt n)\)，然后单个块 \(O(n)\) ，因此最慢也只是被卡到 \(O(n \sqrt n)\)。奇偶优化主要还是卡卡常数，最多就是把块之间的 \(O(n)\) 优化，最多最多优化 \(O(n \sqrt n)\)，实际上肯定没那么多，毕竟，只要理论时间复杂度没问题，不卡常的话一般也是能过得。（卡常就是奇偶优化）

P2709 的代码：

int n,m,k,a[N],id[N],res[N],ans,ot[N];
struct node{int x,y,id;}s[N];
void init(){
	int s=sqrt(n);
	for(int i = 1;i <= n;i++){id[i] = (i-1)/s+1;}
}bool cmp(node a,node b){
	if(id[a.x] == id[b.x]){
		if(id[a.x]&1) return a.y>b.y;
		return a.y<b.y;
	}return id[a.x] < id[b.x];
}void add(int x){ans += 2*res[a[x]]+1;/*完全平方公式*/res[a[x]]++;}
void del(int x){ans -= 2*res[a[x]]-1;res[a[x]]--;}
void solve(){
	cin>>n>>m>>k;
	for(int i = 1;i <= n;i++) cin >> a[i];
	init();
	for(int i = 1;i <= m;i++){
		cin >> s[i].x >> s[i].y;s[i].id=i;
	}sort(s+1,s+1+m,cmp);
	int x=1,y=0;
	for(int i = 1;i <= m;i++){
		while(s[i].x < x) add(--x);
		while(x < s[i].x) del(x++);
		while(s[i].y < y) del(y--);
		while(y < s[i].y) add(++y);
		ot[s[i].id]=ans;
	}for(int i = 1;i <= m;i++) {
		cout<<ot[i]<<endl;
	}
}