四十六（C）

link

考虑第一问。将地图黑白染色，那么每个骨牌占了一黑一白。

删去一个骨牌会得到两个空格。由题目知道，这两个空格位置一一对应一个状态。

我们只需计数有多少种可能的空格出现的方案。考虑一个骨牌移动，等价于将一个空格从头部前一格移到尾部。

那么建图，每个骨牌的头部前一格连向尾部一格，单向边。

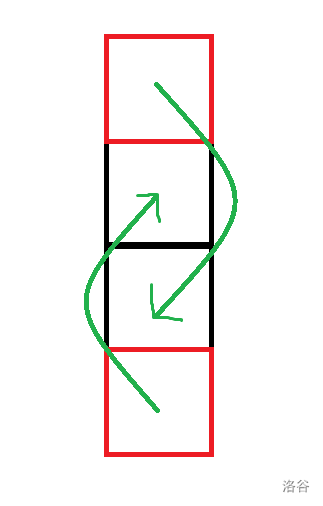
如上图，黑色格子是骨牌，两个方向各一条单向边。

现在空格可以沿着这些单向边移动。注意到边连的两个点是同色的，那么我们就得到了黑白两片森林。

为什么是森林？首先发现这个图每个点入度 \(\le1\)，因此至少是一个外向基环树森林。

考虑如果存在一个环，在网格图中画出这个环围成的封闭图形。会发现，除去边界围住的网格数量是奇数个。

原因考虑扫描线从上往下扫，由于从左边界到右边界只能每次 \(+2\)，每一层的内部格子数一定都是奇数。

同理层数只有奇数层，那么内部格子数就是奇数个。由于第一问没有障碍，在这个环内部不能铺满骨牌，矛盾。

所以就得到了两片森林 \(F_1,F_2\)，问题变成，每次给两个分别在 \(F_1,F_2\) 中的点 \(u,v\)，

则满足 \(u'\in \text{subtree}^{(F_1)}_u,v'\in \text{subtree}^{(F_2)}_v\) 的 \((u',v')\) 都是合法点对，求一共有多少合法点对。

显然直接扫描线求矩形并面积即可。

考虑第二问，现在变成了基环树森林。考虑竖着连的边令其边权为 \(y\)，横着的为 \(x\)，则一个局面的权值为初始局面到它的距离。

题目即要求，\(u\) 到所有能到的点的距离之和。直接预处理即可，有点难写:(

复杂度 \(\Theta(nm\log(nm))\)。