差错控制(检错)
差错从何而来?
概括来说,传输中的差错都是由于噪声引起的。
全局性
由于线路本身电气特性所产生的随机噪声(热噪声),是信道固有的,随机存在的。
解决办法:提高信噪比来减少或避免干扰。(对传感器下手)
局部性
外界特定的短暂原因所造成的冲击噪声,是产生差错的主要原因。
解决办法:通常利用编码技术来解决。
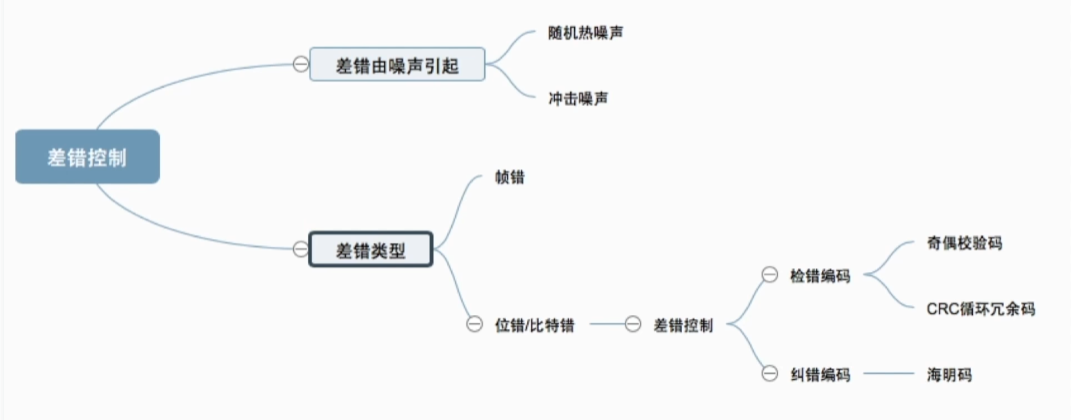
差错种类


差错控制使用的方法
数据链路层编码和物理层的数据编码与调制不同。
物理层编码针对的是单个比特,解决传输过程中比特的同步等问题,如曼彻斯特编码。
而数据链路层的编码针对的是一组比特,它通过冗余码的技术实现一组二进制比特串在传输过程是否出现了差错。
冗余编码
在数据发送之前,先按某种关系附加上一定的冗余位,构成一个符合某一规则的码字后再发送。
当要发送的有效数据变化时,相应的冗余位也随之变化,使码字遵从不变的规则。
接收端根据收到码字是否仍符合原规则,从而判断是否出错。
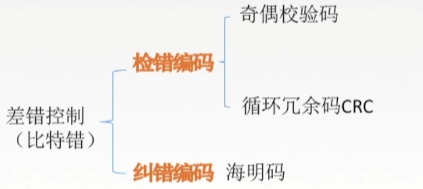
奇偶校验码
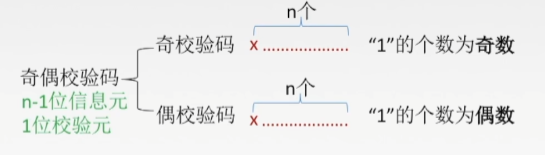
采用奇校验,就是在原先的编码后面(或者前面)加一个1或者0,使得1的个数是奇数
采用偶校验,就是在原先的编码后面(或者前面)加一个1或者0,使得1的个数是偶数
不能保证完全检测,因为有可能
例
如果一个字符s的ASC11编码从低到高依次为1100101,采用奇校验,在下述收到的传输后字符中,哪种错误不能检测?
A. 11000011 B . 11001010 C. 11001100 D.11010011
在原码1100101 后面 加1 得 11001011,这下是奇数了
然后发现ABC,都是4个1,是偶数,肯定不对。
但是D,也是奇数!其实是错了,但是!!!!!检测不到!!!
奇偶校验码特点:只能检查出奇数个比特错误,检错能力为50%。
CRC循环冗余编码
一图流:

1、准备待传有效数据,然后将数据分为等长的组。
2、每个组都加上冗余码(r位FCS)构成帧再发送
- 如何得到r位FCS
先在一组数据后面加上r位的0,假设生成多项式G(x)的阶为r,则加r个0。
以生成多项式(模二AKA异或)
得到一个商和余数,这个余数就是r位FCS

3、接收方检验:d+r位数据,除以生成多项式
4、余数为0则为正确接受,余数不为0则舍弃
例
要发送的数据是1101 0110 11,采用CRC校验,生成多项式是10011,那么最终发送的数据应该是?
首先
计算冗余码
- 加0 。生成多项式是四阶的,加四个零,得到11010110110000
- 模二除法。

就是先写个1,然后异或下来,同0异1。结果首位0不写,向后补位。直到所有的都除出来
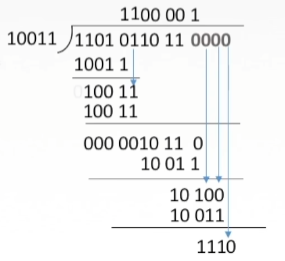
除到这个时候,只剩4位了,就不用除了
1110就叫做4位FCS
然后把FCS冗余码加到后面
于是最终要发送的序列就是1101 0110 11 1110
接收端检错过程
把收到的每一个帧都除以同样的除数(生成多项式,这里是10011),然后检查得到的余数R。
1.余数为0,判定这个帧没有差错,接受。
2.余数为不为0,判定这个帧有差错(无法确定到位),丢弃。
FCS的生成以及接收端CRC检验都是由硬件实现,处理很迅速,因此不会延误数据的传输。
无差错&可靠传输的区别
在数据链路层仅仅使用循环冗余检验CRC差错检测技术,只能做到对帧的无差错接收,即“凡是接收端数据链路层接受的帧,我们都能以非常接近于1的概率认为这些帧在传输过程中没有产生差错”。
接收端丢弃的帧虽然曾收到了,但是最终还是因为有差错被丢弃。“凡是接收端数据链路层接收的帧均无差错”。
“可靠传输” :数据链路层发送端发送什么,接收端就收到什么。
链路层使用CRC检验,能够实现无比特差错的传输,但这还不是可靠传输。
纠错编码——海明码
之前只是知道有错,但是不知道在哪
需要找到位置并且纠正错误。(可以发现双比特错,但是只能纠正单比特错。)

海明距离 (海明距、码距)
两个合法编码(码字)的对应比特取值不同的比特数称为这两个码字的海明距离(码距),
一个有效编码集中,任意两个合法编码(码字)的海明距离的最小值称为该编码集的海明距离(码距)。

在上图中,编码集的码距为1,因为所有的编码的海明距离都是1(001和010,100和101)
码距为1的情况下,无法检查差错?
求得码距的方法:可以肉眼观察,也可以做异或,。例如0000和1001做异或结果1001,有几个1,码距就是多少

在这套编码集中,如果出现了差错,那么是可以检测到的,因为码距出现了减小
码距设置依据:
码距为n,可以检测出n-1位的比特错。
-
想要检查n位比特错,就要设置码距为n+1
-
想要纠正n为比特错,就要设置码距为2n+1
纠错过程
1、确定校验码位数r(海明不等式)

使用穷举法来求得r。m+r便得到海明码。
例
要发送的数据是1100
数据的位数m=4,满足不等式的最小r穷举为3。因为不可能是2!
然后推得D=1100的海明码应该有m+r = 4+3 = 7位
其中原数据4位,校验码3位。
2、确定校验码的位置
校验码放在序号为2^n的位置,数据按序填上。

其中2^0位置是校验码x1, 2^1位置是校验码x2, 2^2位置是校验码x3,
3、求出校验码的值(分组偶校验求值)
- 在刚才的表格上面把序号的二进制写出来:

此时校验码4,2,1所在的位置是100,010,001
发现特点: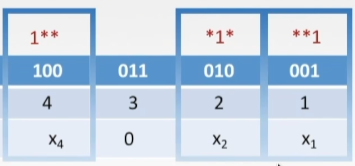
满足1xx的数有:111,110,101,100;
于是就说x4负责4,5,6,7的校验。如此类推,
2号校验码负责2, 3, 6, 7的校验
1号校验码负责1, 3,5, 7的校验
-
刚才就相当于完成了一次分组。
-
对这些分组依次采用偶校验。
x4分组:4567,所在的值是110x。偶校验要求1出现偶数次,那么x就是0。于是x4 = 0
x2分组:2367,所在的值是x011。偶校验要求1出现偶数次,那么x就是0。于是x3 = 0
x1分组:1357,所在的值是x001。偶校验要求1出现偶数次,那么x就是1,。于是x1 = 1
至此得到完整的海明码

4、检错和纠错
例
若接收方收到的数据是:1 1 1 0 0 0 1,检错类似奇偶校验。
4号校验码负责4567的校验,0111,奇,不行
2号校验码负责2367的校验,0011,偶
1号校验码负责1357的校验。1011,奇,不行
检查出错的位置:
- 法一:用维恩图
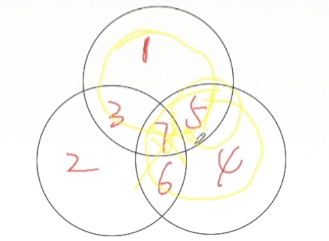
4567错,1357错。错的一定是5或者7
但是2367又没错,所以7不是错的。错的是5!!!!
- 法二:矩阵
首先将

提取成增广矩阵的形式:

然后用偶校验方法,让每一行满足1出现偶数次。
解得
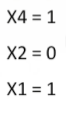
然后将其转置

读取第二行的二进制,101,是5。所以是第五位出错。
总结