首页 > 其他分享 >状压DP

状压DP

时间：2024-02-29 17:24:33浏览次数：22  
标签：状态 DP int 状压 dp leqslant define

状压 $ DP $ 学习笔记

状压，状态压缩，好像很nb的样子

实际上，它就是利用二进制将只有 $ 0 $ 和 $ 1 $ 两种状态的一个序列压缩成一个数来存储。还是不好理解？举个例子，如果在一行棋盘上摆棋子，棋子只有摆与不摆两种状态，则 \((1011)_2\) 即 \((11)_{10}\) 就表示，棋盘的第 $ 1，3，4 $ 个位置摆了棋子，这就是这一行棋子的状压。

做状压 $ DP $ ，首要的是明确状压什么。如果二进制状态有 $ n $ 位，那么实际存状态的十进制数大小就是 $ 2^n-1 $ ,显然， $ n $ 不能很大，所以可以根据数据范围来初步判断要状压谁

对于 $ DP $ 来说，还是要具体题目具体分析，进行状态转移

另外，由于状压用的是二进制，位运算就很重要了……

题单 (学校 $ OJ $ )

$ T_A $ 特殊方格棋盘

题意

在 $ n \times n (n \leqslant 20) $ 的方格棋盘上放置 $ n $ 个车，某些格子不能放，求使它们不能互相攻击的方案总数。

输入

输入文件第一行，有两个数 $ n $ 、 $ m $ ， $ n $ 表示方格棋盘大小, $ m $ 表示不能放的格子数量
下面有 $ m $ 行,每行两个整数,为不能放的格子的位置。

2 1
1 1

输出 $ \ \ \ \ \ \ $ 方案总数

1

思路分析

在棋盘上放车，显然每行每列最多都只能放一个。那么我们用 $ dp_i $ 来表示 当前棋盘上车的状态为 $ i $ 时(若该列已放了车，二进制状态为 $ 1 $ 的方案总数

#include<bits/stdc++.h>
using namespace std;
const int N=(1<<20)+10;
#define ll long long
#define endl '\n'
ll n,m,f[N];
ll a[25];
int count(int x)
{
    int res=0;
    while(x){
        if(x&1)    res++;
        x>>=1;
    }
    return res;
}
int lowbit(int x){
    return x&(-x);
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int u,v;
        cin>>u>>v;
        a[u]+=(1<<(v-1));//状压存储不能放的位置
    }
    f[0]=1;
    for(int i=1;i<=(1<<n)-1;i++)
    {
        int cnt=count(i);//这里cnt为放车的数量，巧的是，这刚好也是当前行数
        for(int j=i;j;j-=lowbit(j))//枚举每一个车
        {
            if(!(a[cnt]&lowbit(j)))//该车位置合法
            {
                int k=i^lowbit(j);
                f[i]+=f[k];
            }
        }
    }
    cout<<f[(1<<n)-1];
    return 0;
}

$ T_B $ 互不侵犯

题意

在 $ N \times N $ 的棋盘里面放 $ K $ 个国王，使他们互不攻击，求共有多少种摆放方案。国王能攻击到它上下左右，以及左上左下右上右下八个方向上附近的各一个格子，共 $ 8 $ 个格子。

$ N \leqslant 9 , k \leqslant N $

输入 $ {\ \ \ \ \ \ \ \ \ }n $ , $ k $

3 2

输出 $ {\ \ \ \ \ \ \ \ \ } $ 方案数

16

思路分析

$ N \leqslant 9 $ ,这么好的范围，必须状压每一行的国王状态啊。国王会攻击左右，因此并不是所有状态都合法，于是我们可以预处理出合法状态。利用一个 $ check() $ 函数检查是否合法，设当前检查的状态为 $ a $ ,由于国王会攻击左一位和右一位，所以只要检验 \(a \&\) $ (a>>1) $ 以及 \(a \&\) \(（a<<1）\) 是否有冲突，如果没有，显然是合法的

下一步，设定 $ dp $ 的状态，令 $ dp_{i,k,j} $ 表示当前枚举到第 $ i $ 行，已经摆了 $ k $ 个国王，最后一行状态为 $ j $

接下来进行 $ DP $ ,由于国王会攻击上下，所以枚举第 $ i $ 行和第 $ i-1 $ 行的状态 $ a,b $ ,检查一下 $ a,b $ 是否冲突，同理。

最后推出转移方程，显然第 $ i $ 行的 $ dp $ 只与第 $ i-1 $ 行有关

第 $ i $ 行，状态为 $ \ i\ ,\ k\ ,\ a\ ,\ \ \ dp_{i,k,a} $

第 $ i-1 $ 行，状态为 $ \ i-1\ ,\ k-cnt(a)\ ,\ b\ \ \ dp_{i-1,k-cnt(a),b} $

加法原理，转移方程则为:

\[dp_{i,k,a}=\sum_{k=1}^m dp_{i-1,k-cnt(a),b} \ \ (k \geqslant cnt(a)) \]

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
ll n,m;
ll dp[10][100][1<<10];
ll king[1000],cnt[1000],sum;
bool check_self(ll a)
{
    if(a&(a>>1))  return 0;
    if(a&(a<<1))  return 0;
    return 1;
}

bool check_ab(ll a,ll b)
{
    if(a&(b>>1))  return 0;
    if(a&(b<<1))  return 0;
    if(a&b)  return 0;
    return 1;
}
ll count(ll x)
{
    ll res=0;
    while(x){
        if(x&1)  res++;
        x>>=1;
    }
    return res;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin>>n>>m;
    ll MAXN=(1<<n)-1;
    for(ll i=0;i<=MAXN;i++)
        if(check_self(i))//预处理合法状态
        {
            king[++sum]=i;
            cnt[sum]=count(i);
            dp[1][cnt[sum]][i]=1;//初始化第一行
        }
    for(ll i=2;i<=n;i++)
        for(ll ja=1;ja<=sum;ja++)
            for(ll jb=1;jb<=sum;jb++)
                for(ll k=0;k<=m;k++)
                {
                    ll a=king[ja];
                    ll b=king[jb];
                    if(check_ab(a,b)&&k>=cnt[ja])
                    {
                        dp[i][k][a]+=dp[i-1][k-cnt[ja]][b];
                    }
                }
    ll ans = 0;
    for (ll i=0;i<=MAXN;++i)
        ans+=dp[n][m][i];
    cout<<ans;
    return 0;
}

$ T_C $ 炮兵阵地

题意

司令部的将军们打算在 的网格地图上部署他们的炮兵部队。一个 $ N \times M $ 的地图由 $ N $ 行 $ M $ 列组成，地图的每一格可能是山地（用 $ H $ 表示），也可能是平原（用 $ P $ 表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

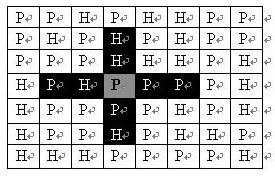
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入

第一行包含两个由空格分割开的正整数，分别表示 $ N $ 和 $ M $ ；
接下来的 $ N $ 行，每一行含有连续的 $ M $ 个字符( $ P $ 或者 $ H $ )，中间没有空格。按顺序表示地图中每一行的数据。

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

输出 $ {\ \ \ \ \ } $ 最多能摆放的炮兵队数

6

思路分析

有了前面两个题的经验，我们肯定要状压存储每一行山地的状态 $ hill[i] $ 。此题就是 $ T_B.plus $ ,道理差不多，只要躲判断一个山地的影响就好了，自己根据 $ T_B $ 推一下,不一样的是，要用 $ dp_{i,j,k} $ 表示到第 $ i $ 行，本行状态为 $ j $ ，上一行状态为 $ k $
转移方程去看\(shadow\)的吧，相信如果你能看懂你就不需要看我的题解了

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define MAXN (1<<m)-1
int n,m;
int hill[110];
int dp[110][110][110];
int p[1000],cnt[1000],sum;
int ans;
bool check_self(int a)
{
    if(a&(a<<1) || a&(a<<2) || a&(a>>1) || a&(a>>2))
        return 0;
    return 1;
}

int count(int x){
    int res=0;
    while(x)
    {
        if(x&1) res++;
        x>>=1;
    }
    return res;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin>>n>>m;
    char c;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            cin>>c;
            if(c=='H')
                hill[i]+=(1<<(j-1));
        }
    for(int i=0;i<=MAXN;i++)
        if(check_self(i))
        {
            p[++sum]=i;
            cnt[sum]=count(i);
            if(!(i & hill[1]))//初始化第1行，与地形不冲突
                dp[1][sum][0]=cnt[sum];
        }
    for(int i=2;i<=n;i++)
        for(int j=1;j<=sum;j++)//第i行状态->j
        {
            if(p[j] & hill[i])
                continue;
            for(int k=1;k<=sum;k++)//第i-1状态->k
            {
                if(p[k] & hill[i-1])
                    continue;
                if(p[k] & p[j])
                    continue;
                if( i == 2 )//代码出了点小bug，特判一下
                    dp[i][j][k]=max(dp[i][j][k],dp[i-1][k][0]+cnt[j]);
                for(int l=1;l<=sum;l++)//第i-2行状态->l
                {
                    if(p[l] & hill[i-2]) 
                        continue;
                    if(p[k] & p[l])
                        continue;
                    if(p[j] & p[l]))
                        continue;
                    //保证都不会冲突
                    dp[i][j][k]=max(dp[i][j][k],dp[i-1][k][l]+cnt[j]);
                }
            }
        }
        //枚举i代替p[i],节省空间
    for(int i=1;i<=sum;i++)
        for(int j=1;j<=sum;j++)
            ans=max(ans,dp[n][i][j]);
    cout<<ans;
    return 0;
}

$ T_D $ 旅游景点

题意

题面太 $ TM $ 长了，概括一下题意：有一个 $ n $ 个节点的带权图， $ 1 $ 为起点， $ n $ 为终点，图中的 $ 2...k+1 $ 为必经点，同时有 $ q $ 组限制，每组包含一个 $ a,b $ ,要求 $ a $ 点必须在 $ b $ 点前经过,求最短路径

输入

第一行包含3个整数 $ N(2\leqslant N\leqslant 20000),M(1\leqslant M\leqslant 200000),K(0\leqslant K\leqslant 20) $ ,意义如上所述。以下 $ M $ 行，每行包含 $ 3 $ 个整数 $ X，Y，Z，(1\leqslant X，Y\leqslant n，0 < Z\leqslant 1000) $ ;

接下来一行，包含一个整数 $ q $ ，表示有 $ q $ 个限制条件 $ (0\leqslant q < n) $ 。以下 $ q $ 行，每行两个整数 $ f，l(1\leqslant l，f\leqslant n) $ ，表示在 $ f $ 停留的时候要在 $ l $ 之前。

8 15 4
1 2 3
1 3 4
1 4 4
1 6 2
1 7 3
2 3 6
2 4 2
2 5 2
3 4 3
3 6 3
3 8 6
4 5 2
4 8 6
5 7 4
5 8 6
3
2 3
3 4
3 5

输出 $ {\ \ \ \ \ \ } $ 最短路径

19

思路分析

$ 2...k+1 $ 节点必经，可以 $ Dijk $ 预处理 $ 2...k+1 $ 之间的的最短路，然后状压已经经过的必经点状态，即 $ dp_{i,j} $ 表示跑到 $ i $ 节点，经过的必经点状态为 $ j $ 的最短路径长度。
转移方程见代码。

#include<bits/stdc++.h>
using namespace std;
const int N=2000010;
#define ll long long
#define endl '\n'
#define MAXN (1<<k)-1
int n,m,k;
struct EDGE{
    int next,to,w;
}e[N];
int tot,head[N];
void add(int u,int v,int w)
{
    tot++;
    e[tot].to=v;
    e[tot].next=head[u];
    head[u]=tot;
    e[tot].w=w;
}
int s[25][25];
int dis[100010];
bool f[100010];
int dp[25][1<<20];
void Dijk(int u)//朴素Dijk会T，要用堆优化
{
    memset(dis,0x3f,sizeof(dis));
    memset(f,0,sizeof(f));
    priority_queue<pair<int,int> > q;
    q.push(make_pair(0,u));
    dis[u]=0;
    while(q.size()){
        int x=q.top().second;
        q.pop();
        if(!f[x])
        {
            f[x]=1;
            for(int i=head[x];i;i=e[i].next){
                int y=e[i].to;
                if(dis[y]>dis[x]+e[i].w){
                    dis[y]=dis[x]+e[i].w;
                    q.push(make_pair(-dis[y],y));
                }
            }
        }
        
    }
    for(int i=1;i<=k+1;i++)
         s[i][u]=s[u][i]=dis[i];
    s[u][0]=dis[n];

}
int front[25];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin>>n>>m>>k;
    memset(dp,-1,sizeof(dp));
    dp[1][0]=0;
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        add(a,b,c);
        add(b,a,c);
    }
    for(int i=1;i<=k+1;i++)
        Dijk(i);
    int q;cin>>q;
    while(q--)
    {
        int a,b;
        cin>>a>>b;
        front[b]+=(1<<(a-2));//记录必须在b之前经过的点
    }
    for(int now=0;now<=MAXN;now++)//现在的状态
        for(int i=1;i<=k+1;i++)//枚举当前在的点
            if(dp[i][now]!=-1)
            {
                for(int j=2;j<=k+1;j++)//枚举下一个跑的点
                {
                    int reach=(now|(1 << (j-2)));
                    if((now & front[j])==front[j])//已经符合要求
                    //位运算一定要加括号……呜呜呜
                        if(dp[j][reach]>dp[i][now]+s[i][j] || dp[j][reach]==-1)
                           dp[j][reach]=dp[i][now]+s[i][j];
                }
            }
    int ans=1e9;
    for(int i=1;i<=k+1;i++)
    {
        if(dp[i][MAXN]!=-1)
            ans=min(ans,dp[i][MAXN]+s[i][0]);
    }
    cout<<ans;
    return 0;
}

学校OJ空间限350MB，但是某LOJ和某谷都限64MB，交上去直接MLE，乐，我也懒得改了

$ T_E $ 愤怒的小鸟

题意

Kiana 最近沉迷于一款神奇的游戏无法自拔。
简单来说，这款游戏是在一个平面上进行的。有一架弹弓位于 \((0,0)\) 处，每次 Kiana 可以用它向第一象限发射一只小鸟，小鸟们的飞行轨迹均为形如 \(y=ax^2+bx\) 的曲线，其中 \(a,b\) 是 Kiana 指定的参数，且必须满足 \(a<0\) 。当小鸟落回地面（即\(x\)轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有\(n\)只猪，其中第\(i\)只猪所在的坐标为 \((x_i,y_i)\) 。如果某只小鸟的飞行轨迹经过了 \((x_i,y_i)\) ，那么第\(i\)只猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；否则这只小鸟飞行的全过程就不会对第\(i\)只猪产生任何影响。

而这个游戏的目的，就是通过发射小鸟消灭所有的猪。

这款神奇游戏的每个关卡对来说都很难，所以 Kiana 还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在「输入格式」中详述(没用)。
假设这款游戏一共有\(T\)个关卡，现在 Kiana 想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的猪。由于她不会算，所以希望由你告诉她。

输入

第一行包含一个正整数\(T\)，表示游戏的关卡总数。
下面依次输入这\(T\)个关卡的信息。每个关卡第一行包含两个非负整数\(n,m\),分别表示该关卡中的猪数量和 Kiana 输入的神秘指令类型。(m没用)
接下来的\(n\)行中，第\(n\)行包含两个正实数，表示第\(i\)只猪坐标为 \((x_i,y_i)\)。数据保证同一个关卡中不存在两只坐标完全相同的猪。

3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00

\(n∈[1,18],m∈[0,2],x_i,y_i∈(0,10)\)

输出 \({\ \ \ \ \ \ \ }\) 一个正整数，表示相应的关卡中，消灭所有猪最少需要的小鸟数量。

2
2
3

思路分析

首先预处理出一条抛物线能打下的小鸟状态，用 \(L_{i,j}\) 表示过\(i,j\)两鸟的抛物线能打下的鸟，状压存储。枚举\(spx\)为已打下的鸟的状态，枚举\(i,j\),那么

\[dp_{spx | L_{i,j}}=min(dp_{spx | L_{i,j}},dp_{spx}+1) \]

怎样预处理\(L\)？枚举\(i,j\),解二元一次方程，解出\(a,b\),再枚举\(k\),如果\(a,b\)分别相等，\(L_{i,j}++\)

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define MAXN (1<<n)-1
double x[20],y[20];
int L[20][20];
int dp[1<<20];
int n,m;
double e=1e-10;
double get_a(int i,int j)
{
    return (x[j]*y[i]-x[i]*y[j])/(x[i]*x[i]*x[j]-x[i]*x[j]*x[j]);
}
double get_b(int i,int j)
{
    return (x[j]*x[j]*y[i]-x[i]*x[i]*y[j])/(x[i]*x[j]*x[j]-x[i]*x[i]*x[j]);
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int T;cin>>T;
    while(T--)
    {
        memset(dp,0x3f,sizeof(dp));
        memset(L,0,sizeof(L));
        cin>>n>>m;
        for(int i=1;i<=n;i++)
        {
            cin>>x[i]>>y[i];
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                if(x[i]==x[j])  continue;
                double a=get_a(i,j);
                double b=get_b(i,j);
                if(a>0)  continue;
                L[i][j]=L[i][j] | (1<<(i-1));
                L[i][j]=L[i][j] | (1<<(j-1));
                for(int k=1;k<=n;k++)
                {
                    if(x[k]==x[i]||x[k]==x[j]) continue;
                    double a1=get_a(i,k);
                    double b1=get_b(i,k);
                    if(a>0)  continue;
                    // if(a==a1 && b==b1)//显然这样写不行
                    if(fabs(a-a1)<=e && fabs(b-b1)<=e)
                        L[i][j]=L[i][j] | (1<<(k-1));
                }
            }
        }
        dp[0]=0;
        for(int spx=0;spx<MAXN;spx++)
        {
            for(int i=1;i<=n;i++)
            {
                if(spx & (1<<(i-1)))
                    continue;
                for(int j=1;j<=n;j++)
                {
                    if(spx & (1<<(j-1)))
                        continue;
                    if(!L[i][j])
                        continue;
                    dp[spx | L[i][j]]=min(dp[spx | L[i][j]],dp[spx]+1);
                }
                dp[spx | (1<<(i-1))]=min(dp[spx | (1<<(i-1))],dp[spx]+1);
            }
        }
        cout<<dp[MAXN]<<endl;
    }

    return 0;
}

标签：状态,DP,int,状压,dp,leqslant,define
From： https://www.cnblogs.com/lty-ylzsx/p/18043624

相关文章

  • 2024-02-29-Linux高级网络编程(3-UDP编程-TFTP、广播、多播)
    3.UDP编程-TFTP、广播、多播3.1TFTP简介、通信过程3.1.1TFTP概述TFTP：简单文件传送协议（TrivialFileTransferProtocol），最初用于引导无盘系统，被设计用来传输小文件特点：基于UDP实现，不进行用户有效性认证数据传输模式：octet：二进制模式netascii：文本模式mail：已经不再支持3......
  • 2024-02-29-Linux高级网络编程(2-UDP编程)
    2.UDP编程2.1字节序概述字节序是指多字节数据的存储顺序分类：小端格式：将低位字节数据存储在低地址（LSB)大端格式：将高位字节数据存储在低地址2.1.1如何判断当前系统的字节序#include<stdio.h>unionun{/*data*/inta;charb;};intmain(intargc......
  • 由POJ1821得出的一些dp优化技巧
    比如for(inti=1;i<=m;i++){ for(intj=0;j<=n;j++){ dp[i][j]=dp[i-1][j]; } for(intl=max(1,s[i]-l[i]+1);l<=s[i];l++){for(intr=s[i];r<=min(n,l+l[i]-1);r++){dp[i][r]=max(dp[i][r],dp[i-1][l-1]+p[i]*(r-l+1));......
  • 14 CodeTON Round 5 (Div. 1 + Div. 2, Rated, Prizes!)C. Tenzing and Balls（dp+前缀
    思路：dp还是挺明显的，思路可以参考最长上升子序列有点dp的感觉\(f[i]\)表示考虑前\(i\)个数，的最大值当前数有两种删或不删不删：\(f[i]=f[i-1]\);删：\(f[i]=max{f[j-1]+i-j+1}\)这个转移是\(O(n^2)\)的显然时间上来不及考虑优化，第一层循环一定是省不了的考虑优化掉第二层循环......
  • 花神的数论题(数位dp)
    花神的数论题题目描述设\(\text{sum}(i)\)表示\(i\)的二进制表示中\(1\)的个数。给出一个正整数\(N\)，花神要问你\(\prod_{i=1}^{N}\text{sum}(i)\)，也就是\(\text{sum}(1)\sim\text{sum}(N)\)的乘积。数据范围\(1\leN\le10^{15}\)。解法首先我们要......
  • 旅游景点 Tourist Attractions （壮压 DP）题解
    简化题意题目链接——不卡内存班题目链接——卡内存版给定\(n\)个点和\(m\)条边组成的无向图，按照一定限制要求停留\(2\simk+1\)共\(k\)个点（可以经过但不停留），求最短的从\(1\)出发到\(n\)的路径长。限制情况如下：共有\(q\)个限制，接下来\(q\)行，每行两个数\(x......
  • 状压dp
    0.位运算1.概述用01数字标志状态2.要求对象状态只能有两种，例如放/不放，正/反等等某一项指标的范围很小3.实际运用后续\(S_i\)一般表示状态（除特殊说明）特殊方格棋盘click组合：我会！\(n!\)先考虑所有格子都能放\(n\leqslant20\)，可以状压\(0\)表示没放，\(1\)表示放......
  • Windows如何检测UDP端口的连通性
    在Windows平台上如何检测UDP端口的连通性呢？其实，平时我们遇到检测TCP端口的连通性的情况比较多，遇到检测UDP端口连通性的情况较少。而且检测UDP端口的连通性比较复杂一点。像检测TCP端口是否连通（放开），Windows平台，一般常用的工具有telnet、psping等工具，而检测UDP端口的工具，在Linux平台......
  • dp练习
    合并类len=2,[k]消消乐类，len=3,[i+1][j-1]else[k]Bracketshttps://vjudge.net/problem/POJ-2955#include<iostream>#include<cstring>usingnamespacestd;intdp[101][101];boolflag=1;boolpei(inti,intj,chara[]){if(a[i]=='('&&......
  • 基于STM32F407MAC与DP83848实现以太网通讯四（STM32F407MAC数据收发与DMA描述符）
    上一章实现的MAC数据包的基础收发功能，但是只是简单的操作了ETH外设的收发包函数并没有深入了解其中的原理逻辑，本章结合STM32F40x文档与STM32F4x7_ETH_Driver驱动库了解MAC的收发包流程。一、描述符列表 在创建描述符列表之前先了解描述符列表的定义，描述符就软件来说就是一个结......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99