首页 > 其他分享 >动态图连通性

动态图连通性

时间：2024-02-27 14:00:12浏览次数：16  
标签：连通性 tx ty int tr 动态图 now op

Describe:

你要维护一张无向简单图（即没有自环，没有重边的无向图）。你被要求加入删除一条边及查询两个点是否连通。

  • 0：加入一条边。保证它不存在。
  • 1：删除一条边。保证它存在。
  • 2：查询两个点是否联通。

允许离线

Solution:

对于离线做法，可以用线段树分治加可撤销并查集，时间仅 \(O(n\log^2 n)\)，虽然不及 LCT 的 \(O(n\log n)\)，但是它好打好调啊！

线段树分治是基于时间的分治。对于一条在 \(l\) 时出现、\(r\) 时消失的一条边，就在线段树对应的 \(\left[l,r\right]\) 上加入该边的影响。当线段树进入该子树时就加入这条边的影响，离开时还原这条边的影响。对于每一条边，因为树深最多为 \(\log n\)，所以每条边的操作复杂度也只有 \(O(\log n)\)，所有边就是 \(O(n\log n)\)。最后对线段树进行递归，处理询问即可。

struct trnode
{
	int l,r,lc,rc;
	PII q;
	std::vector<std::pair<int,int>>id;
}tr[M<<1];int trlen;
#define lc tr[now].lc
#define rc tr[now].rc
void build(int l,int r)
{
	int now=++trlen;
	tr[now]={l,r};
	if(l==r)
		return ;
	int mid=(l+r)>>1;
	lc=trlen+1;build(l,mid);
	rc=trlen+1;build(mid+1,r);
}
void modify(int now,int l,int r,PII op)
{
	if(tr[now].l==l&&tr[now].r==r)
		return tr[now].id.push_back(op),void();
	int mid=(tr[now].l+tr[now].r)>>1;
	if(r<=mid)
		modify(lc,l,r,op);
	else if(l>=mid+1)
		modify(rc,l,r,op);
	else
		modify(lc,l,mid,op),modify(rc,mid+1,r,op);
}
void add_query(int now,int x,PII op)
{
	if(tr[now].l==tr[now].r)
		return tr[now].q=op,void();
	int mid=(tr[now].l+tr[now].r)>>1;
	if(x<=mid)
		add_query(lc,x,op);
	else
		add_query(rc,x,op);
}
void query(int now)
{
	int tp=top;
	for(auto x:tr[now].id)
		merge(x.first,x.second);
	if(tr[now].q.first)
		puts(findfa(tr[now].q.first)==findfa(tr[now].q.second)?"Y":"N");
	if(tr[now].l!=tr[now].r)
		query(lc),query(rc);
	recover(tp);
}

处理联通性当然是非并查集不可。但这里的并查集要求能还原，于是路径压缩优化就不可使用了。路径压缩会失去原有的父子关系，导致无法还原。就比如说是这样的一个图：

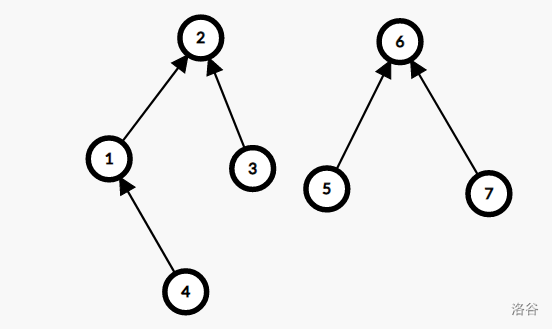
路径压缩后是这样：

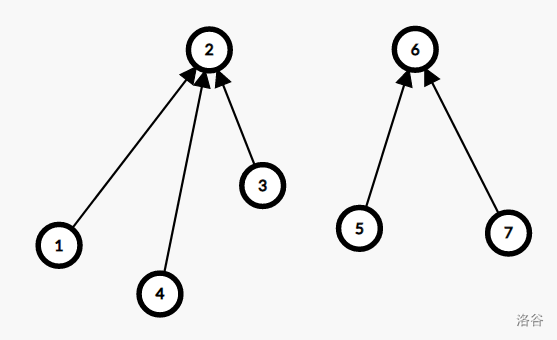
现在加入一条 \(2 \to 6\) 的边：

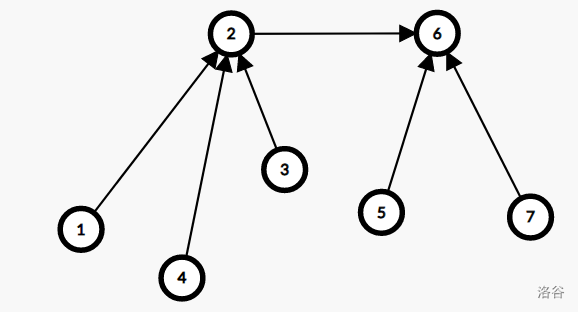
路径压缩后是这样：

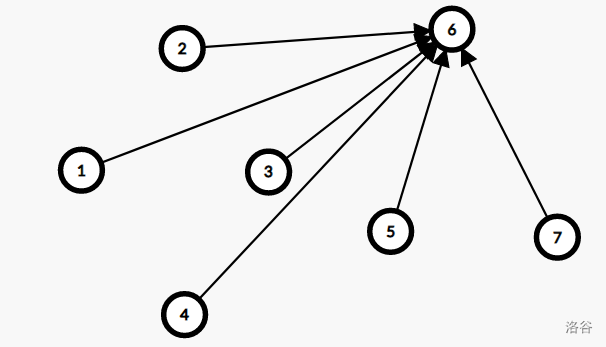
可以看到，\(1,2,3,4\) 的父亲都发生了改变，还原时就需要把它们都还原。这无论是代码复杂度还是时间复杂度都是接受不了的。所以就只能使用按秩合并了。可证明时间复杂度 \(O(\log n)\)。在还原时，可以在全局开一个栈，开一个变量记录当时的栈高，再存下加入的操作，当需要还原时，还原到原先的栈高即可。

int fa[N],siz[N],top;
PII sta[N];
void clear()
{
	for(int i=1;i<=n;i++)
		fa[i]=i,siz[i]=1;
}
int findfa(int x)
{
	return fa[x]==x?x:findfa(fa[x]);
}
void merge(int x,int y)
{
	int tx=findfa(x),ty=findfa(y);
	if(tx==ty)
		return ;
	if(siz[tx]>siz[ty])
	{
		sta[++top]={tx,ty};
		fa[ty]=tx;
		siz[tx]+=siz[ty];
	}
	else
	{
		sta[++top]={ty,tx};
		fa[tx]=ty;
		siz[ty]+=siz[tx];
	}
}
void recover(int tp)
{
	while(top>tp)
	{
		int tx=sta[top].first,ty=sta[top].second;
		fa[ty]=ty;
		siz[tx]-=siz[ty];
		top--;
	}
}

总时间复杂度 \(O(n \log^2 n)\)。

Code:

完整代码如下：

bool _Start;
#include<map>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
namespace IO
{
	#define TP template<typename T>
	#define TP_ template<typename T,typename ... T_>
	#ifdef DEBUG
	#define gc() (getchar())
	#else
	char buf[1<<20],*p1,*p2;
	#define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<20,stdin),p1==p2)?EOF:*p1++)
	#endif
	#ifdef DEBUG
	void pc(const char &c)
	{
		putchar(c);
	}
	#else
	char pbuf[1<<20],*pp=pbuf;
	void pc(const char &c)
	{
		if(pp-pbuf==1<<20)
			fwrite(pbuf,1,1<<20,stdout),pp=pbuf;
		*pp++=c;
	}
	struct IO{~IO(){fwrite(pbuf,1,pp-pbuf,stdout);}}_;
	#endif
	TP void read(T &x)
	{
		x=0;static int f;f=0;static char ch;ch=gc();
		for(;ch<'0'||ch>'9';ch=gc())ch=='-'&&(f=1);
		for(;ch>='0'&&ch<='9';ch=gc())x=(x<<1)+(x<<3)+(ch^48);
		f&&(x=-x);
	}
	TP void write(T x)
	{
		if(x<0)
			pc('-'),x=-x;
		static T sta[35],top;top=0;
		do
			sta[++top]=x%10,x/=10;
		while(x);
		while(top)
			pc(sta[top--]^48);
	}
	TP_ void read(T &x,T_&...y){read(x);read(y...);}
	TP void writeln(const T x){write(x);pc('\n');}
	TP void writesp(const T x){write(x);pc(' ');}
	TP_ void writeln(const T x,const T_ ...y){writesp(x);writeln(y...);}
	TP void debugsp(const T x){fprintf(stderr,"%d ",x);}
	TP void debug(const T x){fprintf(stderr,"%d\n",x);}
	TP_ void debug(const T x,const T_...y){debugsp(x);debug(y...);}
	TP inline T max(const T &a,const T &b){return a>b?a:b;}
	TP_ inline T max(const T &a,const T_&...b){return max(a,max(b...));} 
	TP inline T min(const T &a,const T &b){return a<b?a:b;}
	TP_ inline T min(const T &a,const T_&...b){return min(a,min(b...));}
	TP inline void swap(T &a,T &b){static T t;t=a;a=b;b=t;}
	TP inline T abs(const T &a){return a>0?a:-a;}
	#undef TP
	#undef TP_
}
using namespace IO;
using std::cerr;
using PII=std::pair<int,int>;
using LL=long long;
constexpr int N=5e3+10;
constexpr int M=5e5+10;
int n,m;
int fa[N],siz[N],top;
PII sta[N];
void clear()
{
	for(int i=1;i<=n;i++)
		fa[i]=i,siz[i]=1;
}
int findfa(int x)
{
	return fa[x]==x?x:findfa(fa[x]);
}
void merge(int x,int y)
{
	int tx=findfa(x),ty=findfa(y);
	if(tx==ty)
		return ;
	if(siz[tx]>siz[ty])
	{
		sta[++top]={tx,ty};
		fa[ty]=tx;
		siz[tx]+=siz[ty];
	}
	else
	{
		sta[++top]={ty,tx};
		fa[tx]=ty;
		siz[ty]+=siz[tx];
	}
}
void recover(int tp)
{
	while(top>tp)
	{
		int tx=sta[top].first,ty=sta[top].second;
		fa[ty]=ty;
		siz[tx]-=siz[ty];
		top--;
	}
}
struct trnode
{
	int l,r,lc,rc;
	PII q;
	std::vector<std::pair<int,int>>id;
}tr[M<<1];int trlen;
#define lc tr[now].lc
#define rc tr[now].rc
void build(int l,int r)
{
	int now=++trlen;
	tr[now]={l,r};
	if(l==r)
		return ;
	int mid=(l+r)>>1;
	lc=trlen+1;build(l,mid);
	rc=trlen+1;build(mid+1,r);
}
void modify(int now,int l,int r,PII op)
{
	if(tr[now].l==l&&tr[now].r==r)
		return tr[now].id.push_back(op),void();
	int mid=(tr[now].l+tr[now].r)>>1;
	if(r<=mid)
		modify(lc,l,r,op);
	else if(l>=mid+1)
		modify(rc,l,r,op);
	else
		modify(lc,l,mid,op),modify(rc,mid+1,r,op);
}
void add_query(int now,int x,PII op)
{
	if(tr[now].l==tr[now].r)
		return tr[now].q=op,void();
	int mid=(tr[now].l+tr[now].r)>>1;
	if(x<=mid)
		add_query(lc,x,op);
	else
		add_query(rc,x,op);
}
void query(int now)
{
	int tp=top;
	for(auto x:tr[now].id)
		merge(x.first,x.second);
	if(tr[now].q.first)
		puts(findfa(tr[now].q.first)==findfa(tr[now].q.second)?"Y":"N");
	if(tr[now].l!=tr[now].r)
		query(lc),query(rc);
	recover(tp);
}
int v[N][N];
bool _End;
int main()
{
//	fprintf(stderr,"%.2 MBlf\n",(&_End-&_Start)/1048576.0);
	read(n,m);
	clear();
	build(1,m);
	for(int i=1;i<=m;i++)
	{
		int op,x,y;read(op,x,y);
		switch(op)
		{
			case 0:
				v[x][y]=v[y][x]=i;
				break;
			case 1:
			{
				modify(1,v[x][y],i,{x,y});
				v[x][y]=v[y][x]=0;
				break;
			}
			case 2:
				add_query(1,i,{x,y});
				break;
		}
	}
	for(int i=1;i<=n;i++)
		for(int j=i+1;j<=n;j++)
			if(v[i][j])
				modify(1,v[i][j],m,{i,j});
	query(1);
	return 0;
}

强制在线

Solution:

施工中...（等 AC 了再来写）

标签：连通性,tx,ty,int,tr,动态图,now,op
From： https://www.cnblogs.com/lofty2007/p/18036700

相关文章

  • 图的连通性
    图的连通性这个专题，不太好说，因为涉及到的东西实在是太广泛太杂了，我们这里就只讲建模，至于建模之后的处理方式可以移步至其他的知识点。强连通对于有向图，我们可以发现，如果每个点的贡献和影响与这个点可达的点有关，那么我们就可以将一个强连通分量缩点，将原图转化为一个有向无环图，然......
  • 图论——连通性
    图论——连通性基本知识路径相关途径：连接一串结点的序列称为途径，用点序列\(v_{0..k}\)和边序列\(e_{1..k}\)描述，其中\(e_i=(v_{i-1},v_i)\)，通常写为\(v_0\tov_1\to\cdots\tov_k\)。迹：不经过重复边的途径称为迹。回路：\(v_0=v_k\)的迹称为回路。......
  • MFC 动态图标切换
    主要是学会获取应用实例，然后是定时器的使用。▲会一直变动，4个轮流滚。标题是属于框架的。头文件：private:HICONicon[4];构造函数：CMainFrame::CMainFrame()noexcept{//加载图标//获取应用程序icon[0]=AfxGetApp()->LoadIconW(IDI_ICON1);......
  • 连通性问题
    求割点#include<bits/stdc++.h>usingnamespacestd;typedeflonglongll;constllN=2e4+10;lln,m,dfn[N],low[N],tot,root;boolcut[N];vector<ll>G[N];voidtarjan(llu){ dfn[u]=low[u]=++tot; llflag=0; for(autov:G[u]){ if(!dfn[v]){ ta......
  • Fusion Studio 18.6 (macOS, Windows) - 视觉特效、3D、VR 及动态图形解决方案
    FusionStudio18.6(macOS,Windows)-视觉特效、3D、VR及动态图形解决方案BlackmagicDesignFusionStudio18请访问原文链接：https://sysin.org/blog/fusion/，查看最新版。原创作品，转载请保留出处。作者主页：sysin.orgFusion18登场卓越领先的视觉特效、3D、VR及动态......
  • 网络连通性测试 【Connectivity】
    CFD简介CFD（ConnectivityFaultDetection，连通错误检测）是一种二层网络中的端到端OAM（Operation，Administration，andMaintenance，操作、管理和维护）技术，主要用于在二层网络中检测链路连通性，以及在故障发生时进行定位。适用的二层网络包括基于VLAN的以太网网络和基于MPLS的二层V**。......
  • flutter中背景图片（动态图片）
    单页面设置背景图片使用 Container 组件和 decoration 属性：优点：简单易用，适用于大多数情况下的页面背景设置。缺点：无法控制背景图片的位置和层级。classMyBookextendsStatelessWidget{constMyBook({super.key});@overrideWidgetbuild(BuildContextcontex......
  • Excel动态图表有多少种类型，你知道哪些？
    折线图：折线图是最常见的动态图表类型之一，它可以清晰地展现数据随时间变化的趋势。在Excel中，您可以轻松创建动态折线图，使数据的变化更加生动。柱状图：动态柱状图可以清晰地比较不同类别的数据，并随着数据的变化而自动更新。这种图表类型在展示多个数据项之间的对比时非常有用。饼图：......
  • 连通性容斥
    一种比较牛的东西，典型标志为\(n\le18\)，计数满足特殊性质而且连通的状物。[ARC105F]有一张\(n\)个点\(m\)条边的简单无向图，问选出一个边集，使得\(n\)个点与这些边构成的图连通，并且图是二分图的方案数。\(1\leqn\leq17,n-1\leqm\leq\frac{n(n-1)}{2}\)。通用套路......
  • 自动化ping测网络连通性监测与Excel自动记录
    根据现有提供海量ip进行检测网络质量，如果手动操作那将成为一项很难完成的操作。为了简化这一任务，可以使用Python自动化脚本，利用openpyxl和pythonping库，自动执行ping测试并记录结果到Excel文件。openpyxl:openpyxl是一个用于操作Excel文件的库。它允许你读取、写入和......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99