一到比较水的退火题(虽然也调了 3h)
题意
在平面直角坐标系中,有 \(n\) 条线段,第 \(i\) 条的端点是 \((a_i,b_i)\) 和 $ (c_i,d_i)$,任意线段不共点。(这里笔者为了方便会默认 \(a_i<c_i\))
你要在平面上画一个圆,使得任意一条线段都和圆周或圆内部有至少一个公共点,求满足条件的圆的最小半径
思路
看完题目发现是一道计算几何题,但我不会计算几何怎么办呢,这时候就想到了模拟退火(SA)。
题目其实就是让圆与所有线段相切或相交,那么根据数学九上第三章的知识,判断圆与线段位置关系有三种方法:
-
判断交点个数(相交是有两个交点,相切是有一个交点,相离是有零个交点)
-
判断 \(d\) 与 \(r\) 的关系。(\(d\) 为直线到圆心的距离,\(r\) 为圆的半径)。若 \(d<r\),则是相交,\(d=r\) 则是相切,\(d>r\) 则是相离。
-
切线判定定理(经过半径的外端且垂直于这条半径的直线是圆的切线)
分别进行考虑,首先 3 肯定不行,如果要用 1 的话,应该要建系,再判 Δ,可能可以,但比较烦。再看 2,这个也是求一下解析式,在判断点到直线距离,但在这题中是线段,那也没有关系,进行分类讨论即可。
代码实现
首先在我看来那么一份SA代码大概长这样
#include <bits/stdc++.h>
using namespace std;
const double delta=......;//降温系数,越接近1,SA结果越精确,但时间也会更多
double .........,answ,ansx,ansy;//一大堆变量
int solve(......){//估价函数,就是判断答案是否更优(这里我反而觉得是最不好想的地方, 因为你要优化时间)
...
...
...
}
void sa(){
double x=ansx,y=ansy,end=......;//每次SA时要临时记录一下当前做到的地方,和ansx,ansy不同的是它会跳出去,所以可能近期会跟劣但这也是SA能处理多峰的关键
for(int t=.....;t>=end;t*=delta){//初温,就是你一开始波动会多大,这个可以让你在做多次SA时能跳出原来的最优解
int tx=.....;//根据当前的t来rand()决定与x,y差多少
int ty=.....;
int new_ans=solve(tx,ty);//计算新解
int Delta=new_ans-answ;
if(Delta<0){//若更优,则更新
answ=new_ans;
ansx=x=tx;
ansy=y=ty;
.......
}
else if(exp(-Delta/t)*RAND_MAX<rand()){//否则以一定概率接受新解,此时不能更新ans(用脚想,虽然我之前错了几次)
x=tx;
y=ty;
......
}
}
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin....
...
...
...
while((double)clock()/CLOCKS_PER_SEC<0.96){//用来卡时,保险一点开0.8,平时做题我喜欢卡满
sa();
}
cout<<answ;
return 0;
}
那么我们就根据框架来设计程序
首先我们要把一些功能给做好。如求解析式,平方,求两点距离.......
其次看最简单的主函数(解释代码里有)
srand(time(0));
cin>>n;
for(int i=1;i<=n;i++){
cin>>p[i].xi>>p[i].yi>>p[i].xj>>p[i].yj;
p[i]=work(p[i].xi,p[i].yi,p[i].xj,p[i].yj);//搞出它的解析式
ansx+=p[i].xi;
ansx+=p[i].xj;
ansy+=p[i].yi;
ansy+=p[i].yj;
}
ansx/=(n*2);
ansy/=(n*2);//随便搞一个初始解
answ=solve(ansx,ansy);//算出它的估价函数
while((double)clock()/CLOCKS_PER_SEC<1.7){//因为时限有2s
sa();
}
printf("%.15lf",answ);
return 0;
再来看sa函数
void sa(){
double end=1e-10,x=ansx,y=ansy;//因为这题精度要求还是挺高的,所以末温要小一点
for(double t=300;t>=end;t*=delta){//同上,我的delta是0.99993
double tx=x+t*(2.0*rand()-RAND_MAX)/11451;//因为坐标都小于1000,所以波动不用特别大
double ty=y+t*(2.0*rand()-RAND_MAX)/11451;
double new_ans=solve(tx,ty);
double Delta=new_ans-answ;
if(Delta<0){//正常操作
answ=new_ans;
x=ansx=tx;
y=ansy=ty;
}else if(exp(-Delta/t)*RAND_MAX>rand()){
x=tx,y=ty;
}
}
}
最后就是最难的估价函数了
首先我们要进行分类讨论,因为题目中有可能会有竖着的线段或横着的线段,所以我们要进行特判。
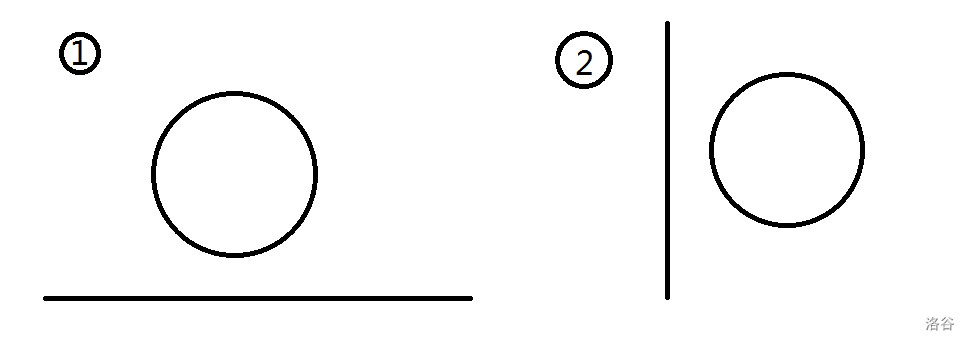
如图1,我们进行分类讨论。设圆心坐标为 \((x,y)\)
- 若 \(x<a_i\),\(d\) 就是圆心与 \((a_i,b_i)\) 的距离
- 若 \(x>c_i\),\(d\) 就是圆心与 \((c_i,d_i)\) 的距离
- 否则,\(d\) 就是 $\left | y-b_i \right | $
如图2,我们进行分类讨论。设圆心坐标为 \((x,y)\)
- 若 \(y<b_i\),\(d\) 就是圆心与 \((a_i,b_i)\) 的距离
- 若 \(y>d_i\),\(d\) 就是圆心与 \((c_i,d_i)\) 的距离
- 否则,\(d\) 就是 \(\left|x-a_i\right|\)
如果就是正常的线段,我们就算出过圆心且与线段垂直的直线的解析式,算出垂足坐标 \((x_i,y_i)\) 再进行分类讨论
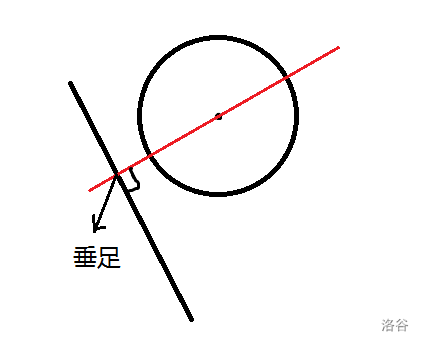
- 若\(x_i<a_i\),\(d\) 就是圆心与 \((a_i,b_i)\) 的距离
- 若\(x_i>c_i\),\(d\) 就是圆心与 \((c_i,d_i)\) 的距离
- 否则,\(d\) 就是圆心到垂足的距离
呼,貌似挺烦的,看下代码吧
double calc(double x,double y,line p){
line q;
if(p.b==114514&&p.k==114514){//特判竖的
if(y>p.yi) return dis(x,y,p.xi,p.yi);
else if(y<p.yj) return dis(x,y,p.xj,p.yj);
else return fabs(x-p.xi);
}
if(p.b==-114514&&p.k==-114514){//特判横的
if(x<p.xi) return dis(x,y,p.xi,p.yi);
else if(x>p.xj) return dis(x,y,p.xj,p.yj);
else return fabs(y-p.yi);
}
q.k=-1/p.k;//垂线的解析式
q.b=y-q.k*x;
double xi=(q.b-p.b)/(p.k-q.k),yi;//垂足坐标
yi=xi*p.k+p.b;
if(xi<p.xi) return dis(p.xi,p.yi,x,y);
else if(xi>p.xj) return dis(x,y,p.xj,p.yj);
else return dis(x,y,xi,yi);
}
double solve(double x,double y){
double tot=0;
for(int i=1;i<=n;i++){//对于每条线段都做一遍
tot=max(tot,calc(x,y,p[i]));
}
return tot;
}
最后献上完整版(有问题欢迎私信哦)
#include<bits/stdc++.h>
using namespace std;
struct line{
double xi,yi,xj,yj;//左右
double k,b;
}p[105];
const double delta=0.99993;
int n;
double ansx,ansy,answ;
line work(double a,double b,double c,double d){
line p;
if(a==c){
p.k=114514;
p.b=114514;
if(b>d) p.xi=a,p.yi=b,p.xj=c,p.yj=d;
else p.xi=c,p.yi=d,p.xj=a,p.yj=b;
return p;
}
if(b==d){
p.k=-114514;
p.b=-114514;
if(a<c) p.xi=a,p.yi=b,p.xj=c,p.yj=d;
else p.xi=c,p.yi=d,p.xj=a,p.yj=b;
return p;
}
p.k=(d-b)/(c-a);
p.b=b-a*p.k;
if(a<c) p.xi=a,p.yi=b,p.xj=c,p.yj=d;
if(a>c) p.xi=c,p.yi=d,p.xj=a,p.yj=b;
return p;
}
double sq(double x){
return x*x;
}
double dis(double a,double b,double c,double d){
return sqrt(sq(a-c)+sq(b-d));
}
double calc(double x,double y,line p){
line q;
if(p.b==114514&&p.k==114514){
if(y>p.yi) return dis(x,y,p.xi,p.yi);
else if(y<p.yj) return dis(x,y,p.xj,p.yj);
else return fabs(x-p.xi);
}
if(p.b==-114514&&p.k==-114514){
if(x<p.xi) return dis(x,y,p.xi,p.yi);
else if(x>p.xj) return dis(x,y,p.xj,p.yj);
else return fabs(y-p.yi);
}
q.k=-1/p.k;
q.b=y-q.k*x;
double xi=(q.b-p.b)/(p.k-q.k),yi;
yi=xi*p.k+p.b;
if(xi<p.xi) return dis(p.xi,p.yi,x,y);
else if(xi>p.xj) return dis(x,y,p.xj,p.yj);
else return dis(x,y,xi,yi);
}
double solve(double x,double y){
double tot=0;
for(int i=1;i<=n;i++){
tot=max(tot,calc(x,y,p[i]));
}
return tot;
}
void sa(){
double end=1e-10,x=ansx,y=ansy;
for(double t=300;t>=end;t*=delta){
double tx=x+t*(2.0*rand()-RAND_MAX)/11451;
double ty=y+t*(2.0*rand()-RAND_MAX)/11451;
double new_ans=solve(tx,ty);
double Delta=new_ans-answ;
if(Delta<0){
answ=new_ans;
x=ansx=tx;
y=ansy=ty;
}else if(exp(-Delta/t)*RAND_MAX>rand()){
x=tx,y=ty;
}
}
}
int main(){
srand(time(0));
cin>>n;
for(int i=1;i<=n;i++){
cin>>p[i].xi>>p[i].yi>>p[i].xj>>p[i].yj;
p[i]=work(p[i].xi,p[i].yi,p[i].xj,p[i].yj);
ansx+=p[i].xi;
ansx+=p[i].xj;
ansy+=p[i].yi;
ansy+=p[i].yj;
}
ansx/=(n*2);
ansy/=(n*2);
answ=solve(ansx,ansy);
while((double)clock()/CLOCKS_PER_SEC<1.7){
sa();
}
printf("%.15lf",answ);
return 0;
}