自己第一道不看题解写出来的紫题,庆祝一下(没初始化种子导致调了30min)
这是一个 fhq-treap 的题解
思路来源:
首先看题目,因为是序列上的问题,不难想到是一道数据结构题。
首先看到操作 C:对于这种操作,我们可以用平衡树解决,具体方法是,将树 split 成 \(<min,min \le x \le max,>max\) 这三个部分,这个操作可以用按权值分裂解决,答案就是 \(ry\) 的子树大小(\(rx,ry,rz\)表示分裂出来的三棵树)。
其次考虑操作 F:我们可以把操作分成三部分
-
分裂出一颗满足树上权值大于 $ \ge h$ 的子树(直接按 \(val\) split)
-
找出权值前 \(c\) 大的点(直接按 \(siz\) split)
-
将树上每一个点加一
这是就会有聪明的小朋友要问了,操作 F 不是 \(O(n)\) 的吗?但是这个区间加让我们想到 lazytag,所以我们可以用 lazytag 将复杂度优化到 \(O(\log{n})\)
代码实现
思路可行,代码貌似也不难
看到操作 C 不难得出
split(root,x-1,rx,ry);
split(ry,y,ry,rz);
cout<<size[ry]<<endl;
root=merge(merge(rx,ry),rz);
看到操作 F 很快啊,我就把思路模拟出来了,可是连样例都没过。此时我们想到两颗 fhq-treap 能 merge 的前提是以 \(l\) 为根的子树的权值小于等于以 \(r\) 为根的子树。区间加的操作会破坏这个性质。这个也好解决,我们按照最暴力的方法:
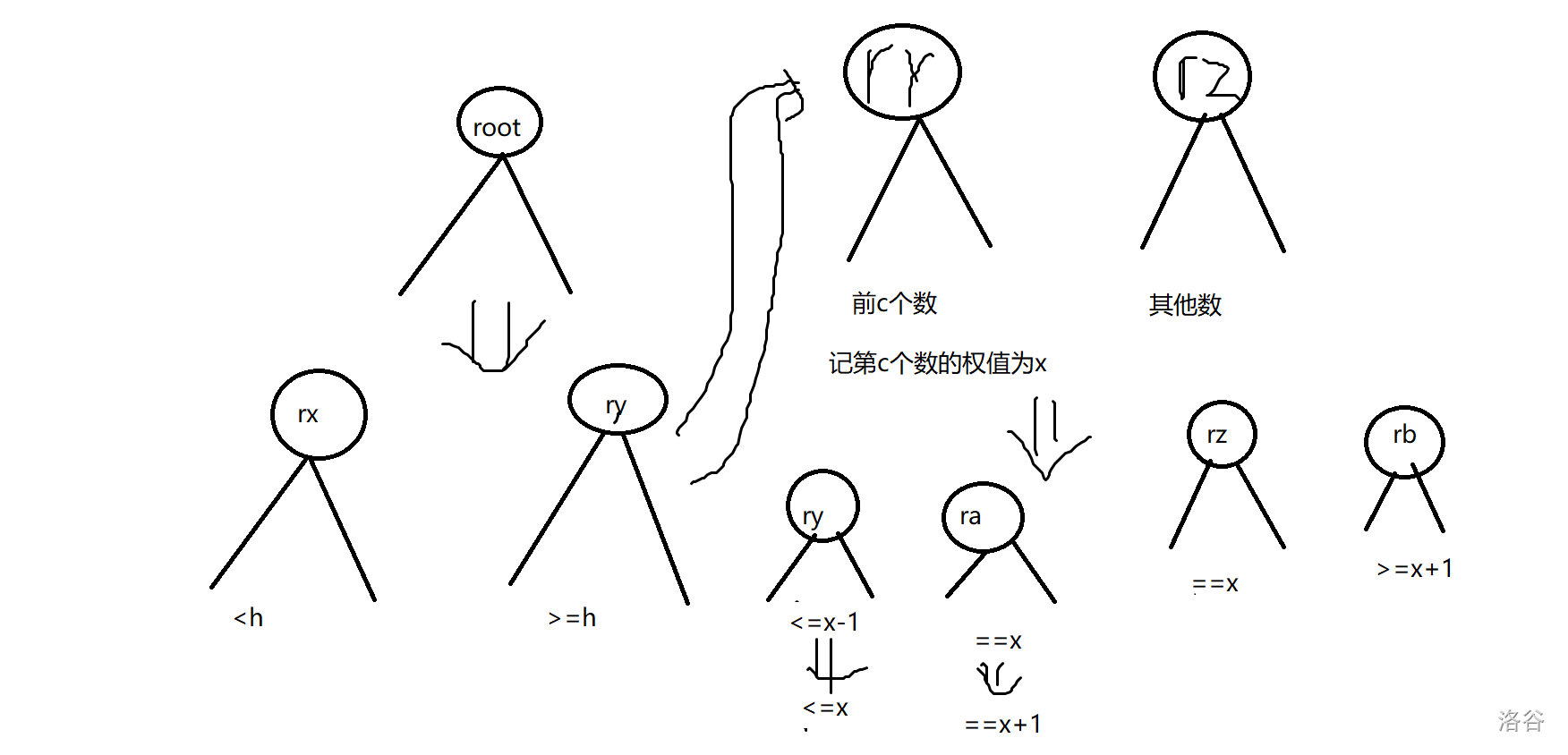
这样就可以合并了:
split(root,y-1,rx,ry);
if(!ry) continue;
split1(ry,x,ry,rz);
la[ry]++;
p[ry].val++;
gg=p[getrnk(ry,size[ry])].val;
split(ry,gg-1,ry,ra);
split(rz,gg,rz,rb);
root=merge(merge(merge(merge(rx,ry),rz),ra),rb);
最后附上完整版(有问题多多留言哦)
#include<bits/stdc++.h>
using namespace std;
struct node{
int val,rd;
}p[100005];
int n,m,x,y,cnt=0,rx,ry,rz,ra,rb,root,gg;
int size[100005],son[100005][2],la[100005];
char op;
inline int read(){
int x=0; bool flag=1; char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}
while(ch>='0'&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0'; ch=getchar();}
if(flag) return x;
return ~(x-1);
}inline void write(int x){
if(x<0) {x=~(x-1); putchar('-');}
if(x>9) write(x/10);
putchar(x%10+'0');
}
void push_up(int x){
size[x]=size[son[x][0]]+size[son[x][1]]+1;
}
void push_down(int x){
if(la[x]!=0){
p[son[x][0]].val+=la[x];
p[son[x][1]].val+=la[x];
la[son[x][0]]+=la[x];
la[son[x][1]]+=la[x];
la[x]=0;
}
}
int add(int x){
cnt++;
p[cnt].rd=rand();
p[cnt].val=x;
size[cnt]=1;
return cnt;
}
void split(int rt,int key,int &x,int &y){
if(!rt){
x=y=0;
return;
}
push_down(rt);
if(p[rt].val<=key){
x=rt;
split(son[rt][1],key,son[rt][1],y);
}else{
y=rt;
split(son[rt][0],key,x,son[rt][0]);
}
push_up(rt);
}
void split1(int rt,int siz,int &x,int &y){
if(!rt){
x=y=0;
return;
}
push_down(rt);
if(size[son[rt][0]]+1<=siz){
x=rt;
split1(son[rt][1],siz-(size[son[rt][0]]+1),son[rt][1],y);
}else{
y=rt;
split1(son[rt][0],siz,x,son[rt][0]);
}
push_up(rt);
}
int merge(int l,int r){
if(!l||!r){
return l+r;
}
push_down(l),push_down(r);
if(p[l].rd<p[r].rd){
son[l][1]=merge(son[l][1],r);
push_up(l);
return l;
}else{
son[r][0]=merge(l,son[r][0]);
push_up(r);
return r;
}
}
int getrnk(int x,int k){
while(true){
push_down(x);
if((size[son[x][0]]+1)==k){
return x;
}else if((size[son[x][0]]+1)<k){
k-=(size[son[x][0]]+1);
x=son[x][1];
}else x=son[x][0];
}
}
int main(){
srand(time(0));
n=read(),m=read();
for(int i=1;i<=n;i++){
x=read();
split(root,x,rx,ry);
root=merge(merge(rx,add(x)),ry);
}
while(m--){
op=getchar();
x=read(),y=read();
if(op=='F'){
split(root,y-1,rx,ry);
split1(ry,x,ry,rz);
la[ry]++;
p[ry].val++;
gg=p[getrnk(ry,size[ry])].val;
split(ry,gg-1,ry,ra);
split(rz,gg,rz,rb);
root=merge(merge(merge(merge(rx,ry),rz),ra),rb);
}else{
split(root,x-1,rx,ry);
split(ry,y,ry,rz);
write(size[ry]);
putchar('\n');
root=merge(merge(rx,ry),rz);
}
}
return 0;
}