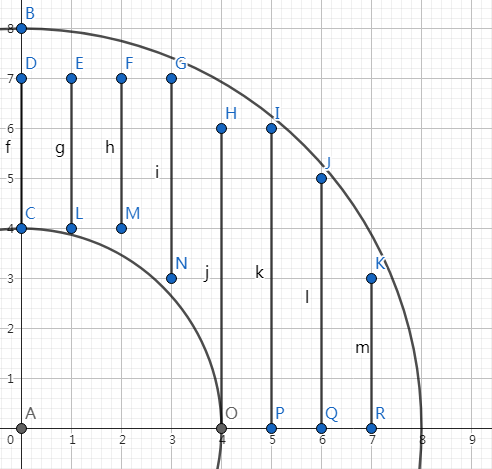
可以看成是求值域两个半圆间的排列的个数。
首先对于每个 \(i\) 设 \(L_i,R_i\) 表示 \(p_i\) 取值的下界和上界。
如果没有小圆的限制即没有下界,问题很简单:把 \(R\) 从小到大排序,然后 \(\prod_{i=1}^nR_i-i+1\) 即为答案,原因显然,因为前面已经选了 \(i-1\) 个并且前 \(i-1\) 个值域 \(\leq R_i\)。
现在加入了 \(L\) 的限制,考虑容斥,用 \(\leq R_i\) 的答案减去 \(\leq L_i-1\) 的答案即为原问题的答案。容斥系数为钦定为 \(L_i-1\) 的位置的个数,其余正常算。
但是因为上面的公式只有在上界有序的情况下(即知道每个限制最终的排名)才能使用,实际上选的是:
-
\([0,n]\) 中选了一些 \(L-1\)。
-
\([0,n]\) 中剩下的部分的选了 \(R\)。
-
\([n+1,2n-1]\) 中因为没有下界限制无法进行容斥,所以都选的是 \(R\)。
这样三个部分内部都是有序的,而且第 \(2\) 部分一定是最大的。所以我们需要把 \(1,3\) 进行一个类似归并的过程来计算方案数。
把 \([n+1,2n-1]\) 的 \(R_i\) 挂在 \([0,n]\) 最后一个满足 \(L_j-1\geq R_i\) 的 \(j\) 上,设 \(f_{i,j}\) 为考虑了 \([i,n]\) 中所有数,钦定了 \(j\) 个做容斥,带容斥系数的方案数。\(f_{i,j}\) 应当计算的部分是上一步挂在 \([i,n]\) 上的所有 \(R\) 的贡献,\([i,n]\) 内容斥的 \(L\) 的贡献和 \([i,n]\) 内没有容斥的 \(R\) 的贡献。
但是直接做有一个问题:计算方案数使用开头的那个 \(\prod R_i-i+1\) 的公式算的,但是在 \([i,n]\) 内没有容斥的 \(R\) 计算途中并不知道他的排名。
如果已知最后要容斥几个,那 \([i,n]\) 内没有容斥的 \(R\) 的排名在 dp 过程中就已知了。可以最外层枚举目的要容斥 \(k\) 个,这样内层进行 dp,\(f_{i,j}\) 意义和上面一样,但是这里可以不带容斥系数,因为我们最后只会用到 \(f_{1,k}\)。
外层枚举复杂度 \(\mathcal O(n)\),内层 dp \(\mathcal O(n^2)\),总复杂度 \(\mathcal O(n^3)\)。
int n,M,ans,lim,L[510],R[510],a[510],f[510][510];
vector<int> ve[510];
inline void mian()
{
read(n,M);
for(int i=0;i<2*n;++i)
{
R[i+1]=sqrt(4*n*n-i*i)+1;
if(i<n)L[i+1]=ceil(sqrt(n*n-i*i))+1;
else L[i+1]=1;
}
R[1]--;
for(int i=2*n;i>=n+2;--i)
{
if(R[i]>=L[1]){!lim?lim=i:0;ve[0].eb(R[i]);continue;}
for(int j=n+1;j>=1;--j)
if(L[j]-1>=R[i]){ve[j].eb(R[i]);break;}
}
for(int i=n+1;i>=1;--i)a[i]=a[i+1]+ve[i].size();
for(int i=0;i<=n;++i)
{
memset(f,0,sizeof(f)),f[n+1][0]=1;
for(int l=0;l<(int)ve[0].size();++l)
f[n+1][0]=1ll*f[n+1][0]*(ve[0][l]-l-i-a[1])%M;
for(int j=n+1;j>=1;--j)
{
for(int k=0;k<=i;++k)
{
for(int l=0;l<(int)ve[j].size();++l)
f[j][k]=1ll*f[j][k]*(ve[j][l]-a[j+1]-k-l)%M;
if(k<i&&L[j]-1-k>0)
f[j-1][k+1]=(f[j-1][k+1]+1ll*f[j][k]*(L[j]-1-k-a[j])%M+M)%M;
f[j-1][k]=(f[j-1][k]+1ll*f[j][k]*(R[j]-(2*n-(j-(i-k)))))%M;
}
}
if(i&1)ans=(ans-f[0][i]+M)%M;
else ans=(ans+f[0][i])%M;
}
write(ans);
}