如果⼀个机器学习模型运⾏良好,为什么我们仅仅信任该模型⽽忽略为什么做出特定的决策呢?
诸如分类准确性之类的单⼀指标⽆法完整地描述⼤多数实际任务。当涉及到预测模型时,需要作出权衡:你是只想知道预测是什么?例如,客户流失的概率或某种药物对病⼈的疗效。还是想知道为什么做出这样的预测?这种情况下可能为了可解释性付出预测性能下降的代价。在某些情况下,你不必关⼼为什么要做出这样的预测,只要知道模型在测试数据集的预测性能良好就⾜够了。但是在其他情况下,了解 “为什么” 可以帮助你更多地了解问题、数据以及模型可能失败的原因。有些模型可能不需要解释,因为它们是在低风险的环境中使⽤的,这意味着错误不会造成严重后果 (例如,电影推荐系统),或者该⽅法已经被⼴泛研究和评估 (例如,光学字符识别 OCR)。对可解释性的需求来⾃问题形式化的不完整性,这意味着对于某些问题或任务,仅仅获得预测结果是不够的。该模型还必须解释是怎么获得这个预测的,因为正确的预测只部分地解决了你的原始问题。
机器学习可解释性
需要建立一个解释器来解释黑盒模型,并且这个解释器必须满足以下特征:
可解释性
要求解释器的模型与特征都必须是可解释的,像决策树、线性模型都是很适合拿来解释的模型;而可解释的模型必须搭配可解释的特征,才是真正的可解释性,让不了解机器学习的人也能通过解释器理解模型。
局部保真度
既然我们已经使用了可解释的模型与特征,就不可能期望简单的可解释模型在效果上等同于复杂模型(比如原始CNN分类器)。所以解释器不需要在全局上达到复杂模型的效果,但至少在局部上效果要很接近,而此处的局部代表我们想观察的那个样本的周围。
与模型无关
这里所指的是与复杂模型无关,换句话说无论多复杂的模型,像是SVM或神经网络,该解释器都可以工作。
除了传统的特征重要性排序外,ICE、PDP、SDT、LIME、SHAP都是揭开机器学习模型黑箱的有力工具。
- 特征重要性计算依据某个特征进行决策树分裂时,分裂前后的信息增益(基尼系数);
- ICE和PDP考察某项特征的不同取值对模型输出值的影响;
- SDT用单棵决策树解释其它更复杂的机器学习模型;
- LIME的核心思想是对于每条样本,寻找一个更容易解释的代理模型解释原模型;
- SHAP的概念源于博弈论,核心思想是计算特征对模型输出的边际贡献;
1、机器学习可解释性--LIME
2、机器学习可解释性--SHAP
机器学习可解释性--SHAP
目录1、Shapley Value
沙普利值[1](Shapley value),是通过考虑各个代理(agent)做出的贡献,来公平地分配合作收益。代理的沙普利值是对于一个合作项目所期望的贡献量的平均值。计算公式:
设\(I={1,2...n}\)为\(n\)个人的集合那么\(i\)的贡献为:
其中\(S_{i}\)是\(I\)中包含成员\(i\)的所有子集形成的集合,\(w(|s|)\)是加权因子,\(s\i\)表示集合\(s\)中去掉元素\(i\)后的集合。
\(v(s)-v(s\i)\)成员i在联盟中的贡献,即成员i的边际贡献;\(w(|s|)\)权重\(w(|s|=\frac{(|s|-1)!(n-|s|)!}{n!})\)
WiKi:
玩家联盟合作,并从合作中获得一定的整体收益。由于一些参与者可能比其他参与者对联盟贡献更多,或者可能拥有不同的议价能力(例如威胁要摧毁全部盈余),因此在任何特定博弈中,参与者之间产生的盈余的最终分配应该是什么?或者换句话说:每个参与者对整体合作有多重要,他或她可以合理预期的回报是什么?Shapley 值为这个问题提供了一个可能的答案。
1、https://en.wikipedia.org/wiki/Shapley_value
《可解释的机器学习》
开源地址:
2、https://github.com/MingchaoZhu/InterpretableMLBook
在线阅读:
3、https://hjezero.github.io/posts/32fedbdb/
借助《可解释的机器学习》中例子,假设准备购买一间公寓,其中你所感兴趣的是:1、有无公园;2、公寓面积;3、公寓所位于的楼层;4、是否能养猫。而后对公寓价格预测。

⼀套 50 平⽅⽶的公寓,附近有公园以及禁⽌猫⼊内,预计价格为 300,000 欧元
那么1、公寓面积;2、公寓楼层;3、养猫?4、公园?这4个特征对预测价格300000欧元的贡献是怎么样的呢?
比如说[2]:一个程序C=500行代码需要编写,今天产品经理找了三个程序猿来完成,按照完成量发奖金:
条件一:\(V_{1}=100\),\(V_{2}=125\),\(V_{3}=50\)
解释:1号屌丝程序猿独立能写100行,2号大神程序猿独立能写125行,3号美女程序猿能写50行
条件二:\(V_{12}=270\),\(V_{23}=350\),\(V_{13}=375\)
解释:1,2号合作能写270行,2,3号合作能写350行,1,3号合作能写375行
条件三:\(V_{123}=500\)
3个人共同能完成500行
那么根据3组条件,合计6种组合分别如下:
A.1号程序猿邀请2号程序猿加入他组成S联盟,1,2号邀请3号加入共同编写。
B.1号邀请3号加入成为S小组,2号加入S小组
C.2号邀请1号加入成为S小组,3号加入S小组
D.2号邀请3号加入成为S小组,1号加入S小组
E.3号邀请1号加入成为S小组,2号加入S小组
F.3号邀请2号加入成为S小组,1号加入S小组
计算边际贡献:根据公式1得到: 1的shapley value: $\frac{1}{6}(100+100+145+150+325+150)=\frac{970}{6}$
依次类推得到其他人的shapely value
2、A Unified Approach to Interpreting Model Predictions
SHAP Value与LIME的方法类似,都是通过定义简单模型去对复杂模型进行解释。
“we must use a simpler explanation model, which we define as any interpretable approximation of the original model.” (Lundberg 和 Lee, 2017, p. 2)
我们必须使用一个更简单的解释模型,我们将其定义为对原模型的任何可解释的近似。
回顾LIME模型,利用简单函数\(g\)去在\(x\)“周围”去对复杂函数\(f\)进行局部近似。在本论文作者将部分解释模型函数称为Additive feature attribution methods其形式形如:
\[g(z)=\phi_{0}+\sum_{i=1}^{M}\phi_{i}z_{i} \]其中:\(M\)所有的简单输入特征的个数;\(\phi_{i}\)每一种特征的贡献(对于的shapely值);通过计算所有特征的贡献去近似复杂函数\(f(x)\)
论文中部分解释模型函数有:
1、LIME模型对贡献计算:
\[\xi(s)= argmin_{g\in G} L(f,g,\pi_{x})+\Omega(g) \]2、DeepLIFT(面向深度学习的可解释方法)模型对贡献计算:
\[\sum_{i=1}^{n}C_{\Delta x_{i}\Delta o}=\Delta o \]贡献为:\(C_{\Delta x_{i}\Delta o}\),其中\(o=f(x)\)为模型的输出,其中\(r\)为参考的样本输入,\(\Delta o=f(x)-f(r)\)。
3、经典Shapley Value计算:
- Shapley regression values
feature importances for linear models in the presence of multicollinearity.
此模型要求计算模型所有的特征,认为每一个特征在模型中都起到了作用。计算公式如下:> 就是上面列子中提及到的计算方法 * Shapley sampling values * Quantitative Input Influence
对于additive feature attribution methods存在如下三点性质:
1、Local accuracy
2、Missingness
3、Consistency
Kernel SHAP(Linear LIME + Shapley values)
Kernel SHAP计算步骤:
※1. 初始化一些数据, z', 作为Simplified Features(随机生成(0,1,1,0),(1,0,1,1)等)
其中:\(z'_{k}\in{(0,1)}^{M}\)(0:缺失特征;1:初始化中存在的特征)其中\(M\)是我们的维数(理解为样本特征数目),\(k\in{(1,...K)}\)代表生成数据个数
※2. 将上面的Simplified Features转换到原始数据空间, 并计算对应的预测值, f(h(z'))
比如说上面卖房子例子,有四个特征所以\(M=4\)那么假设初始化为\(z'_{1}=(0,1,1,0)\)那么也就是存在第二和第三个特征的联盟,那么对于第一个和第四个则通过\(h\)函数进行转换
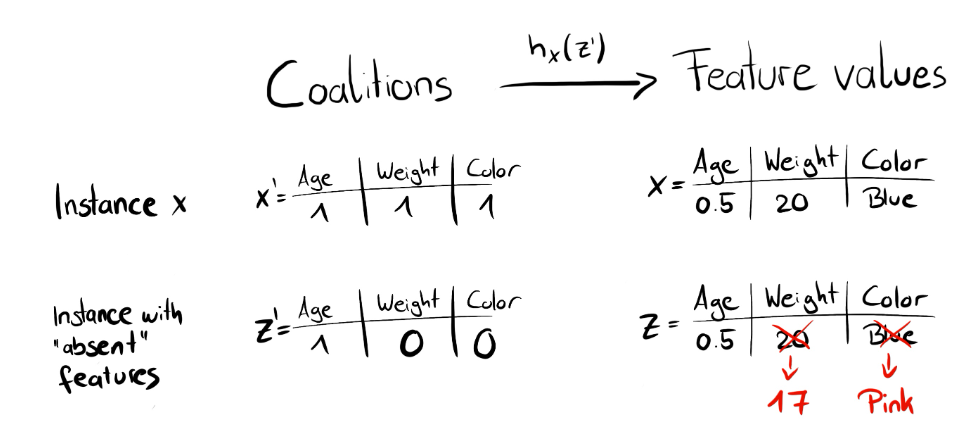
※3. 对每一个z'计算对应的权重
Kernel SHAP的权重函数\(\pi\)为:\(\pi_{x^{'}}(z^{'})=\frac{M-1}{(M\;choose\;|z^{'}|)(M-|z^{'}|)}\),其中\(M\)为维数(所有特征的个数),\(|z^{'}|\)代表样本中1的个数,\(M\;choose\;|z^{'}|\)代表\(C_{M}^{z^{'}}|z^{'}|\)。容易得到:若有很多1或很多0则取较高的权重,若0和1数量相近则取较低的权重。
LIME则是通过距离设置权重
※4. 拟合线性模型
※5. 计算出每一个特征的Shapley Value, 也就是线性模型的系数
Kernel SHAP计算
损失函数:
\[L(f,g,\pi_x^{'})=\sum_{z^{'} \in Z}[f(h_{x}^{-1}(z^{'}))-g(z^{'})]^{2}\pi_{x}^{'}(z^{'}) \]代码
参考
1、https://github.com/MingchaoZhu/InterpretableMLBook
2、https://www.zhihu.com/question/23180647
3、[关于Shapley Value(夏普利值)的公式 - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/483891565#:~:text=Shapley Value公式如下: 记 I%3D { 1%2C2%2C...%2Cn}为n个合作人的集合 varphi_i (upsilon),- upsilon (s backslash { i })]})
4、https://e0hyl.github.io/BLOG-OF-E0/LIMEandSHAP/
5、https://mathpretty.com/10699.html
推荐阅读
1、https://christophm.github.io/interpretable-ml-book