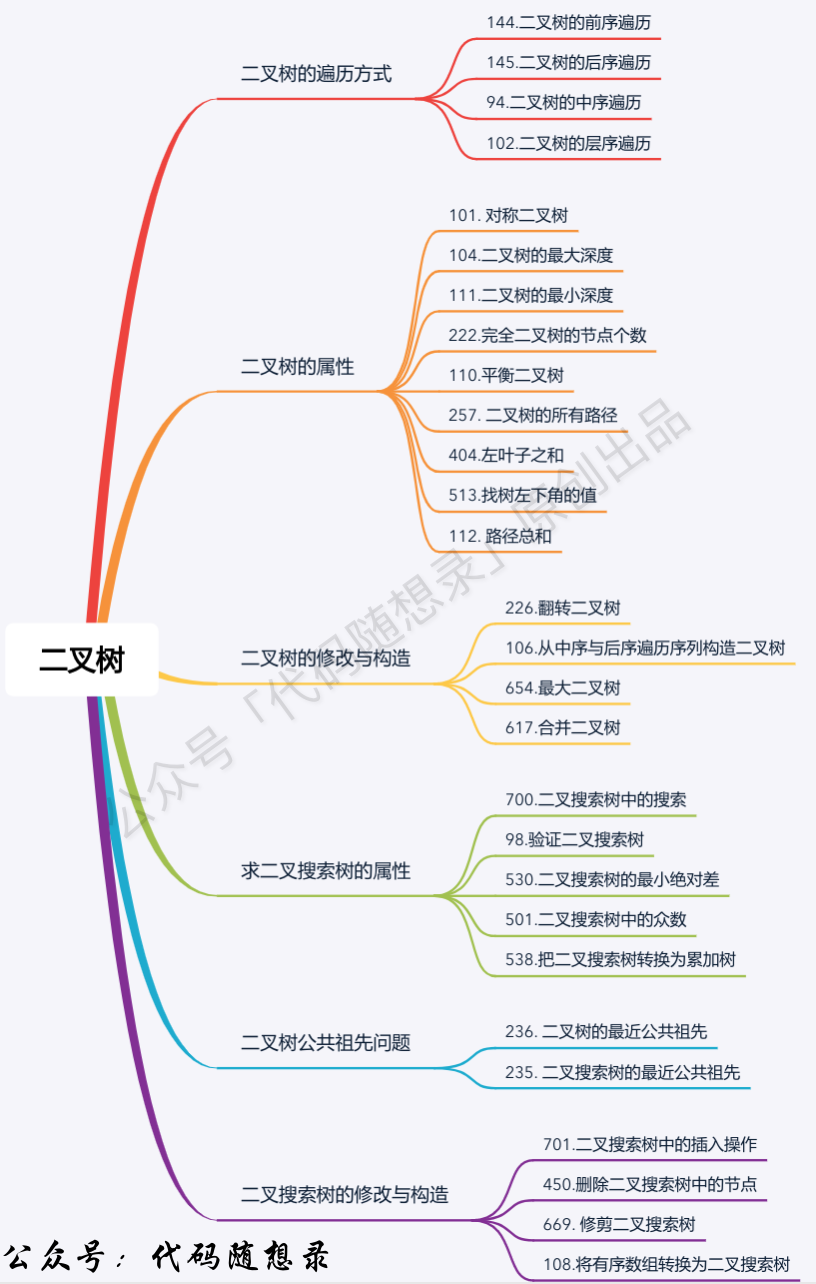
cal的题目分类
说到二叉树,大家对于二叉树其实都很熟悉了,本文呢我也不想教科书式的把二叉树的基础内容再啰嗦一遍,所以以下我讲的都是一些比较重点的内容。
相信只要耐心看完,都会有所收获。
C++中map、set、multimap,multiset的底层实现都是平衡二叉搜索树,所以map、set的增删操作时间时间复杂度是logn,注意我这里没有说unordered_map、unordered_set,unordered_map、unordered_set底层实现是哈希表。
所以大家使用自己熟悉的编程语言写算法,一定要知道常用的容器底层都是如何实现的,最基本的就是map、set等等,否则自己写的代码,自己对其性能分析都分析不清楚!
链式存储如图:
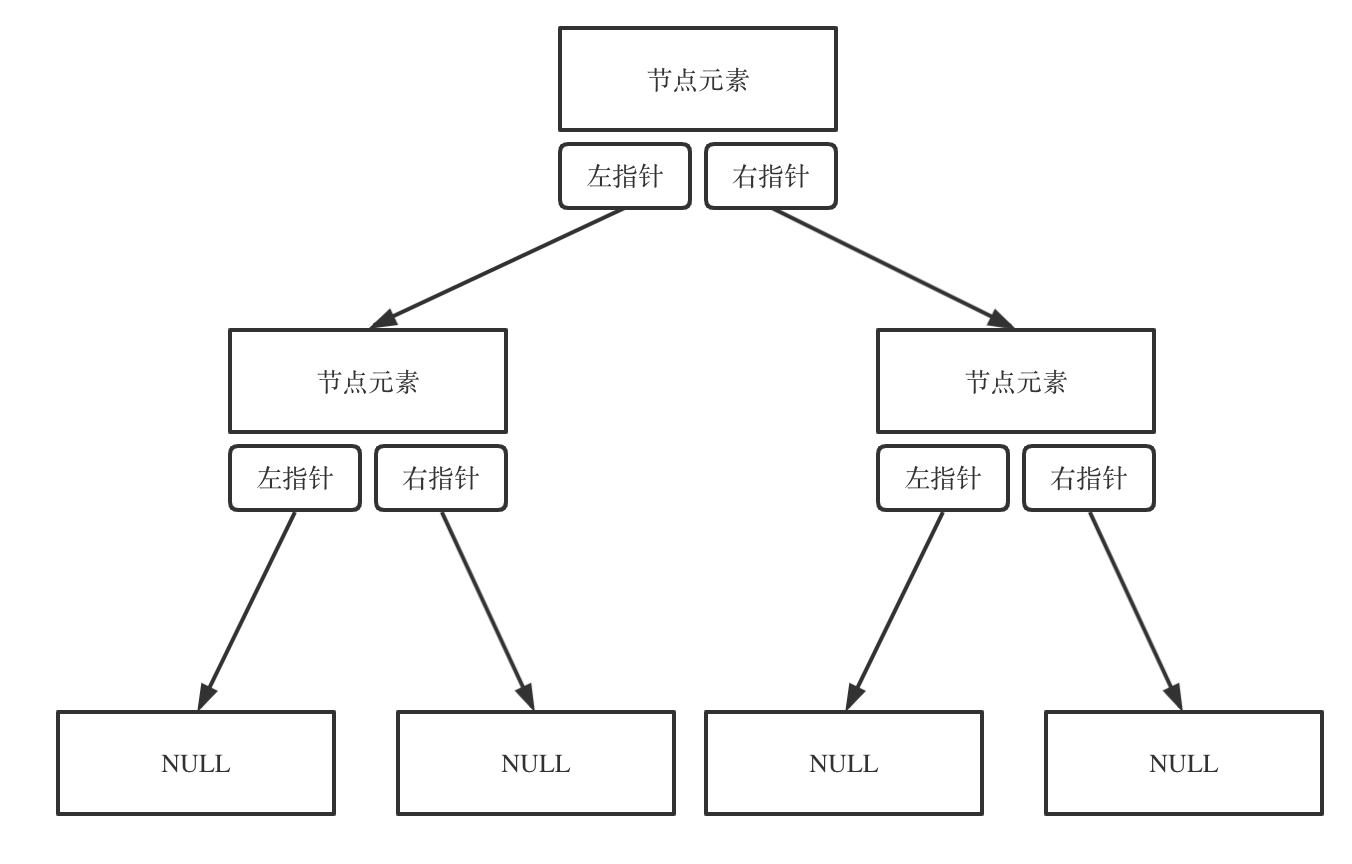
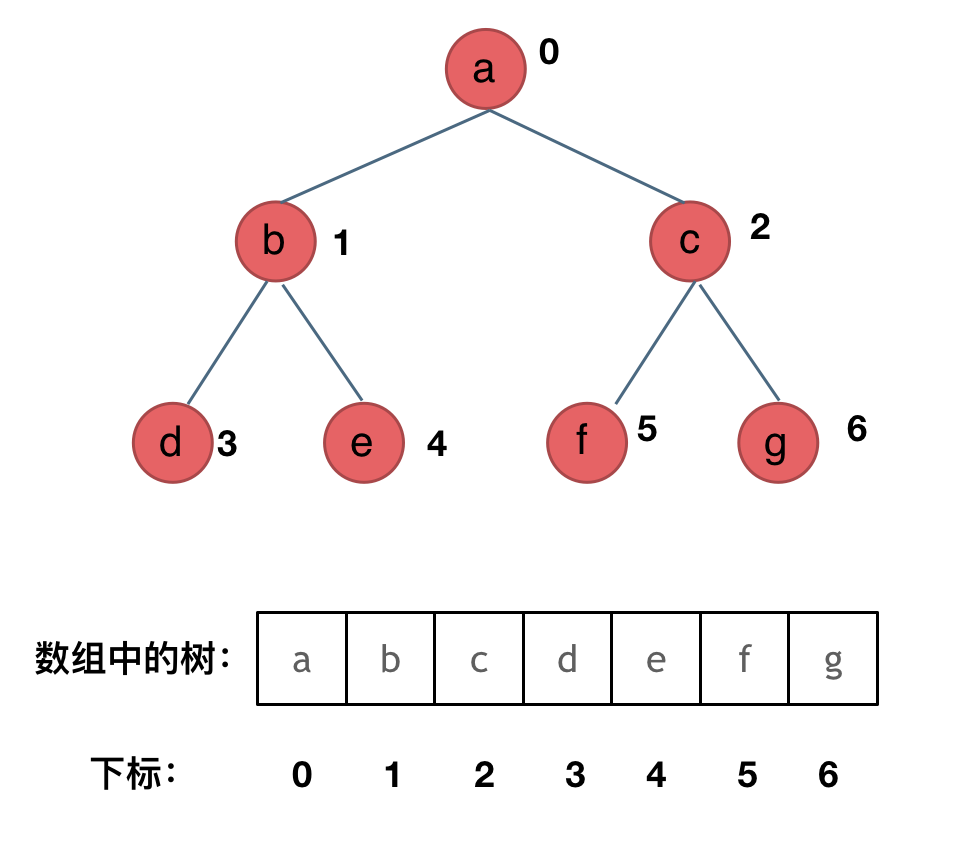
链式存储是大家很熟悉的一种方式,那么我们来看看如何顺序存储呢?
其实就是用数组来存储二叉树,顺序存储的方式如图:
二叉树主要有两种遍历方式:
深度优先遍历:先往深走,遇到叶子节点再往回走。
广度优先遍历:一层一层的去遍历。
这两种遍历是图论中最基本的两种遍历方式,后面在介绍图论的时候 还会介绍到。
那么从深度优先遍历和广度优先遍历进一步拓展,才有如下遍历方式:
深度优先遍历
前序遍历(递归法,迭代法)
中序遍历(递归法,迭代法)
后序遍历(递归法,迭代法)
广度优先遍历
层次遍历(迭代法)
在深度优先遍历中:有三个顺序,前中后序遍历, 有同学总分不清这三个顺序,经常搞混,我这里教大家一个技巧。
这里前中后,其实指的就是中间节点的遍历顺序,只要大家记住 前中后序指的就是中间节点的位置就可以了。
看如下中间节点的顺序,就可以发现,中间节点的顺序就是所谓的遍历方式
前序遍历:中左右
中序遍历:左中右
后序遍历:左右中
大家可以对着如下图,看看自己理解的前后中序有没有问题。
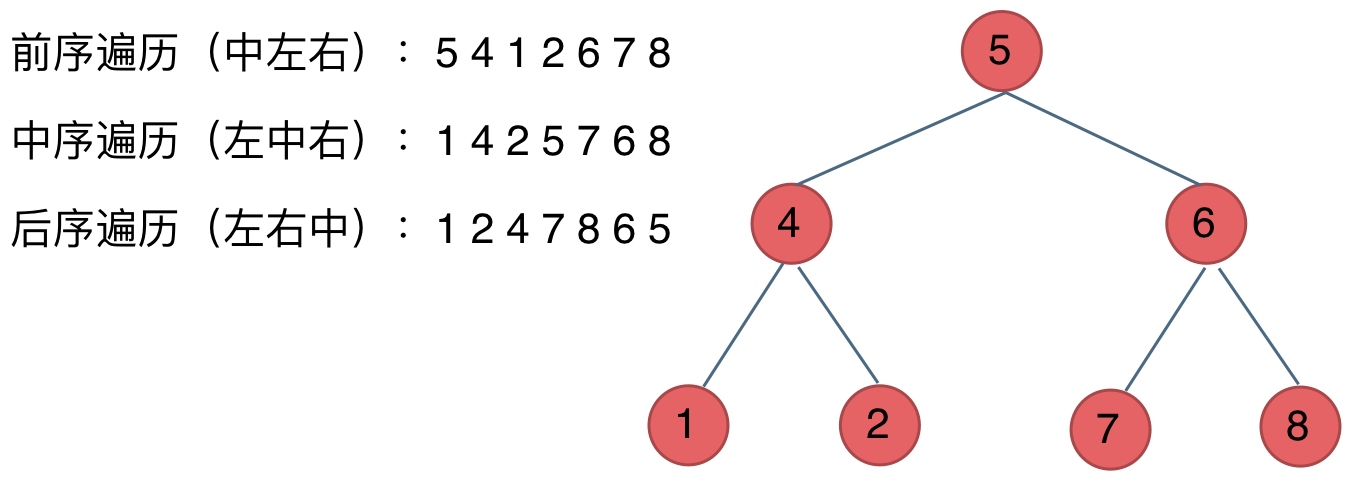
最后再说一说二叉树中深度优先和广度优先遍历实现方式,我们做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的。
之前我们讲栈与队列的时候,就说过栈其实就是递归的一种实现结构,也就说前中后序遍历的逻辑其实都是可以借助栈使用递归的方式来实现的。
而广度优先遍历的实现一般使用队列来实现,这也是队列先进先出的特点所决定的,因为需要先进先出的结构,才能一层一层的来遍历二叉树。
这里其实我们又了解了栈与队列的一个应用场景了。
具体的实现我们后面都会讲的,这里大家先要清楚这些理论基础。
二叉树的递归遍历
思路
这次我们要好好谈一谈递归,为什么很多同学看递归算法都是“一看就会,一写就废”。
主要是对递归不成体系,没有方法论,每次写递归算法 ,都是靠玄学来写代码,代码能不能编过都靠运气。
本篇将介绍前后中序的递归写法,一些同学可能会感觉很简单,其实不然,我们要通过简单题目把方法论确定下来,有了方法论,后面才能应付复杂的递归。
这里帮助大家确定下来递归算法的三个要素。每次写递归,都按照这三要素来写,可以保证大家写出正确的递归算法!
确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
好了,我们确认了递归的三要素,接下来就来练练手:
以下以前序遍历为例:
确定递归函数的参数和返回值:因为要打印出前序遍历节点的数值,所以参数里需要传入vector来放节点的数值,除了这一点就不需要再处理什么数据了也不需要有返回值,所以递归函数返回类型就是void,代码如下:
void traversal(TreeNode* cur, vector<int>& vec)
确定终止条件:在递归的过程中,如何算是递归结束了呢,当然是当前遍历的节点是空了,那么本层递归就要结束了,所以如果当前遍历的这个节点是空,就直接return,代码如下:
if (cur == NULL) return;
确定单层递归的逻辑:前序遍历是中左右的循序,所以在单层递归的逻辑,是要先取中节点的数值,代码如下:
vec.push_back(cur->val);// 中
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
单层递归的逻辑就是按照中左右的顺序来处理的,这样二叉树的前序遍历,基本就写完了,再看一下完整代码:
前序遍历:
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
};
void traversal(struct TreeNode* cur, int* vec, int* index) {
if (cur == NULL) return;
vec[(*index)++] = cur->val; // 中
traversal(cur->left, vec, index); // 左
traversal(cur->right, vec, index); // 右
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
int* result = (int*)malloc(1000 * sizeof(int)); // 假设最多有1000个节点
*returnSize = 0;
traversal(root, result, returnSize);
return result;
}
中序遍历:
void traversal(struct TreeNode* cur, int* vec, int* index) {
if (cur == NULL) return;
traversal(cur->left, vec, index); // 左
vec[(*index)++] = cur->val;// 中
traversal(cur->right, vec, index); // 右
}
后序遍历:
void traversal(TreeNode* cur, int* vec, int* index) {
if (cur == NULL) return;
traversal(cur->left, vec, index); // 左
traversal(cur->right, vec, index); // 右
vec[(*index)++] = cur->val;// 中
}
二叉树的迭代遍历
为什么可以用迭代法(非递归的方式)来实现二叉树的前后中序遍历呢?
我们在栈与队列:匹配问题都是栈的强项 (opens new window)中提到了,递归的实现就是:每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中,然后递归返回的时候,从栈顶弹出上一次递归的各项参数,所以这就是递归为什么可以返回上一层位置的原因。
此时大家应该知道我们用栈也可以是实现二叉树的前后中序遍历了。
前序遍历(迭代法)
我们先看一下前序遍历。
前序遍历是中左右,每次先处理的是中间节点,那么先将根节点放入栈中,然后将右孩子加入栈,再加入左孩子。
为什么要先加入 右孩子,再加入左孩子呢? 因为这样出栈的时候才是中左右的顺序。
动画如下:

#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
} TreeNode;
typedef struct Node {
TreeNode* treeNode;
struct Node* next;
} Node;
typedef struct Stack {
Node* top;
} Stack;
void initStack(Stack* stack) {
stack->top = NULL;
}
int isStackEmpty(Stack* stack) {
return (stack->top == NULL);
}
void push(Stack* stack, TreeNode* treeNode) {
Node* node = (Node*)malloc(sizeof(Node));
node->treeNode = treeNode;
node->next = stack->top;
stack->top = node;
}
TreeNode* pop(Stack* stack) {
if (isStackEmpty(stack)) {
return NULL;
}
TreeNode* treeNode = stack->top->treeNode;
Node* temp = stack->top;
stack->top = stack->top->next;
free(temp);
return treeNode;
}
int* preorderTraversal(TreeNode* root, int* returnSize) {
if (root == NULL) {
*returnSize = 0;
return NULL;
}
int* result = (int*)malloc(1000 * sizeof(int)); // 假设最多有1000个节点
*returnSize = 0;
Stack stack;
initStack(&stack);
push(&stack, root);
while (!isStackEmpty(&stack)) {
TreeNode* node = pop(&stack);
result[(*returnSize)++] = node->val; // 中
if (node->right) push(&stack, node->right); // 右(空节点不入栈)
if (node->left) push(&stack, node->left); // 左(空节点不入栈)
}
return result;
}
int main() {
// 示例用法
TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
root->val = 1;
root->left = (TreeNode*)malloc(sizeof(TreeNode));
root->left->val = 2;
root->left->left = NULL;
root->left->right = NULL;
root->right = (TreeNode*)malloc(sizeof(TreeNode));
root->right->val = 3;
root->right->left = NULL;
root->right->right = NULL;
int returnSize;
int* result = preorderTraversal(root, &returnSize);
printf("Preorder Traversal Result: \n");
for (int i = 0; i < returnSize; i++) {
printf("%d ", result[i]);
}
// 释放内存
free(root->left);
free(root->right);
free(root);
free(result);
return 0;
}
此时会发现貌似使用迭代法写出前序遍历并不难,确实不难。
此时是不是想改一点前序遍历代码顺序就把中序遍历搞出来了?
其实还真不行!
但接下来,再用迭代法写中序遍历的时候,会发现套路又不一样了,目前的前序遍历的逻辑无法直接应用到中序遍历上。
中序遍历(迭代法)
为了解释清楚,我说明一下 刚刚在迭代的过程中,其实我们有两个操作:
处理:将元素放进result数组中
访问:遍历节点
分析一下为什么刚刚写的前序遍历的代码,不能和中序遍历通用呢,因为前序遍历的顺序是中左右,先访问的元素是中间节点,要处理的元素也是中间节点,所以刚刚才能写出相对简洁的代码,因为要访问的元素和要处理的元素顺序是一致的,都是中间节点。
那么再看看中序遍历,中序遍历是左中右,先访问的是二叉树顶部的节点,然后一层一层向下访问,直到到达树左面的最底部,再开始处理节点(也就是在把节点的数值放进result数组中),这就造成了处理顺序和访问顺序是不一致的。
那么在使用迭代法写中序遍历,就需要借用指针的遍历来帮助访问节点,栈则用来处理节点上的元素。
动画如下:

中序遍历,可以写出如下代码:
include <stdio.h>
include <stdlib.h>
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// 创建一个新的树节点
struct TreeNode* createNode(int val) {
struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
newNode->val = val;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
// 递归插入节点
struct TreeNode* insert(struct TreeNode* root, int val) {
if (root == NULL) {
return createNode(val);
}
if (val < root->val) {
root->left = insert(root->left, val);
} else if (val > root->val) {
root->right = insert(root->right, val);
}
return root;
}
// 创建栈
struct TreeNode** createStack(int* top, int size) {
struct TreeNode** stack = (struct TreeNode**)malloc(size * sizeof(struct TreeNode*));
*top = -1;
return stack;
}
// 入栈
void push(struct TreeNode** stack, int* top, struct TreeNode* node) {
stack[++(*top)] = node;
}
// 出栈
struct TreeNode* pop(struct TreeNode** stack, int* top) {
return stack[(*top)--];
}
// 中序遍历二叉树
int* inorderTraversal(struct TreeNode* root, int* returnSize) {
int* result = NULL;
int index = 0;
int top = -1;
struct TreeNode** stack = createStack(&top, 100); // 创建大小为 100 的栈
struct TreeNode* cur = root;
result = (int*)malloc(100 * sizeof(int)); // 分配大小为 100 的结果数组
while (cur != NULL || top != -1) { // 当当前节点不为空或栈不为空时继续遍历
if (cur != NULL) {
push(stack, &top, cur); // 入栈当前节点
cur = cur->left; // 移动到当前节点的左子节点
} else {
cur = pop(stack, &top); // 出栈并将出栈节点赋给当前节点
result[index++] = cur->val; // 将出栈节点的值存入结果数组
cur = cur->right; // 移动到当前节点的右子节点
}
}
free(stack); // 释放栈的内存
*returnSize = index; // 将结果数组的大小赋给返回的大小指针
return result; // 返回结果数组
}
int main() {
struct TreeNode* root = NULL;
root = insert(root, 4);
root = insert(root, 2);
root = insert(root, 6);
root = insert(root, 1);
root = insert(root, 3);
root = insert(root, 5);
root = insert(root, 7);
int returnSize;
int* result = inorderTraversal(root, &returnSize); // 进行中序遍历
printf("Inorder Traversal: ");
for (int i = 0; i < returnSize; i++) {
printf("%d ", result[i]); // 输出中序遍历结果
}
printf("\n");
free(result); // 释放结果数组的内存
return 0;
}
后序遍历(迭代法)
再来看后序遍历,先序遍历是中左右,后续遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中了,如下图:

所以后序遍历只需要前序遍历的代码稍作修改就可以了,代码如下:
#include <stdio.h>
#include <stdlib.h>
// 定义二叉树节点的结构
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// 创建一个新的树节点
struct TreeNode* createNode(int val) {
struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
newNode->val = val;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
// 入栈操作
void push(struct TreeNode** stack, int* top, struct TreeNode* node) {
stack[++(*top)] = node;
}
// 出栈操作
struct TreeNode* pop(struct TreeNode** stack, int* top) {
return stack[(*top)--];
}
// 后序遍历二叉树的函数
int* postorderTraversal(struct TreeNode* root, int* returnSize) {
// 创建大小为 100 的栈
struct TreeNode** stack = (struct TreeNode**)malloc(100 * sizeof(struct TreeNode*));
int top = -1;
int* result = (int*)malloc(100 * sizeof(int)); // 分配大小为 100 的结果数组
int index = 0;
// 如果根节点为空,直接返回空结果数组
if (root == NULL) {
*returnSize = index;
return result;
}
// 将根节点入栈
push(stack, &top, root);
// 进行后序遍历
while (top != -1) {
struct TreeNode* node = pop(stack, &top);
result[index++] = node->val; // 将当前节点的值存入结果数组
if (node->left)
push(stack, &top, node->left); // 左子节点入栈
if (node->right)
push(stack, &top, node->right); // 右子节点入栈
}
free(stack); // 释放栈的内存
// 将结果数组反转
int i = 0, j = index - 1;
while (i < j) {
int temp = result[i];
result[i] = result[j];
result[j] = temp;
i++;
j--;
}
*returnSize = index; // 将结果数组的大小赋给返回的大小指针
return result; // 返回结果数组
}
int main() {
// 创建二叉树节点
struct TreeNode* root = createNode(1);
root->right = createNode(2);
root->right->left = createNode(3);
// 进行后序遍历
int returnSize;
int* result = postorderTraversal(root, &returnSize);
// 输出后序遍历的结果
printf("Postorder Traversal: ");
for (int i = 0; i < returnSize; i++) {
printf("%d ", result[i]);
}
printf("\n");
free(result); // 释放结果数组的内存
return 0;
}
总结
此时我们用迭代法写出了二叉树的前后中序遍历,大家可以看出前序和中序是完全两种代码风格,并不像递归写法那样代码稍做调整,就可以实现前后中序。
这是因为前序遍历中访问节点(遍历节点)和处理节点(将元素放进result数组中)可以同步处理,但是中序就无法做到同步!
上面这句话,可能一些同学不太理解,建议自己亲手用迭代法,先写出来前序,再试试能不能写出中序,就能理解了。
那么问题又来了,难道 二叉树前后中序遍历的迭代法实现,就不能风格统一么(即前序遍历 改变代码顺序就可以实现中序 和 后序)?
当然可以,这种写法,还不是很好理解,我们将在下一篇文章里重点讲解,敬请期待!
二叉树的统一迭代法
思路
此时我们在二叉树:一入递归深似海,从此offer是路人 (opens new window)中用递归的方式,实现了二叉树前中后序的遍历。
在二叉树:听说递归能做的,栈也能做! (opens new window)中用栈实现了二叉树前后中序的迭代遍历(非递归)。
之后我们发现迭代法实现的先中后序,其实风格也不是那么统一,除了先序和后序,有关联,中序完全就是另一个风格了,一会用栈遍历,一会又用指针来遍历。
实践过的同学,也会发现使用迭代法实现先中后序遍历,很难写出统一的代码,不像是递归法,实现了其中的一种遍历方式,其他两种只要稍稍改一下节点顺序就可以了。
其实针对三种遍历方式,使用迭代法是可以写出统一风格的代码!
重头戏来了,接下来介绍一下统一写法。
我们以中序遍历为例,在二叉树:听说递归能做的,栈也能做! (opens new window)中提到说使用栈的话,无法同时解决访问节点(遍历节点)和处理节点(将元素放进结果集)不一致的情况。
那我们就将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。
如何标记呢,就是要处理的节点放入栈之后,紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法。
迭代法中序遍历
中序遍历代码如下:(详细注释)
#include <stdio.h>
#include <stdlib.h>
// 定义二叉树节点的结构
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// 创建一个新的树节点
struct TreeNode* createNode(int val) {
struct TreeNode* newNode = (struct TreeNode*)malloc(sizeof(struct TreeNode));
newNode->val = val;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
// 入栈操作
void push(struct TreeNode** stack, int* top, struct TreeNode* node) {
stack[++(*top)] = node;
}
// 出栈操作
struct TreeNode* pop(struct TreeNode** stack, int* top) {
return stack[(*top)--];
}
// 中序遍历二叉树的函数
int* inorderTraversal(struct TreeNode* root, int* returnSize) {
// 创建大小为 100 的栈
struct TreeNode** stack = (struct TreeNode**)malloc(100 * sizeof(struct TreeNode*));
int top = -1;
int* result = (int*)malloc(100 * sizeof(int)); // 分配大小为 100 的结果数组
int index = 0;
// 如果根节点为空,直接返回空结果数组
if (root == NULL) {
*returnSize = index;
return result;
}
// 将根节点入栈
push(stack, &top, root);
// 进行中序遍历
while (top != -1) {
struct TreeNode* node = stack[top];
if (node != NULL) {
stack[top] = NULL;
if (node->right)
push(stack, &top, node->right); // 右子节点入栈
push(stack, &top, node); // 中节点入栈
push(stack, &top, NULL); // 空节点作为标记,表示中节点访问过
if (node->left)
push(stack, &top, node->left); // 左子节点入栈
} else {
pop(stack, &top); // 弹出空节点
node = stack[top]; // 获取栈中下一个节点
pop(stack, &top); // 弹出节点
result[index++] = node->val; // 将节点值存入结果数组
}
}
free(stack); // 释放栈的内存
*returnSize = index; // 将结果数组的大小赋给返回的大小指针
return result; // 返回结果数组
}
int main() {
// 创建二叉树节点
struct TreeNode* root = createNode(1);
root->right = createNode(2);
root->right->left = createNode(3);
// 进行中序遍历
int returnSize;
int* result = inorderTraversal(root, &returnSize);
// 输出中序遍历的结果
printf("Inorder Traversal: ");
for (int i = 0; i < returnSize; i++) {
printf("%d ", result[i]);
}
printf("\n");
free(result); // 释放结果数组的内存
return 0;
}
看代码有点抽象我们来看一下动画(中序遍历):

动画中,result数组就是最终结果集。
可以看出我们将访问的节点直接加入到栈中,但如果是处理的节点则后面放入一个空节点, 这样只有空节点弹出的时候,才将下一个节点放进结果集。
此时我们再来看前序遍历代码。
迭代法前序遍历
迭代法前序遍历代码如下: (注意此时我们和中序遍历相比仅仅改变了两行代码的顺序)
#include <stdio.h>
#include <stdlib.h>
// 定义二叉树节点的结构
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// 定义栈结构
struct Stack {
struct TreeNode* data[100];
int top;
};
// 初始化栈
void initStack(struct Stack* stack) {
stack->top = -1;
}
// 入栈操作
void push(struct Stack* stack, struct TreeNode* node) {
stack->data[++(stack->top)] = node;
}
// 出栈操作
struct TreeNode* pop(struct Stack* stack) {
return stack->data[(stack->top)--];
}
// 判断栈是否为空
int isEmpty(struct Stack* stack) {
return (stack->top == -1);
}
// 前序遍历二叉树的函数
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
// 分配大小为 100 的结果数组和栈
int* result = (int*)malloc(100 * sizeof(int));
struct Stack stack;
initStack(&stack);
int index = 0;
if (root != NULL) {
push(&stack, root); // 根节点入栈
}
while (!isEmpty(&stack)) {
struct TreeNode* node = pop(&stack); // 弹出栈顶节点
if (node != NULL) {
result[index++] = node->val; // 中节点值存入结果数组
if (node->right) {
push(&stack, node->right); // 右子节点入栈
}
if (node->left) {
push(&stack, node->left); // 左子节点入栈
}
}
}
*returnSize = index; // 将结果数组的大小赋给返回的大小指针
return result; // 返回结果数组
}
int main() {
// 创建二叉树节点
// ...
// 进行前序遍历
int returnSize;
int* result = preorderTraversal(root, &returnSize);
// 输出前序遍历的结果
printf("Preorder Traversal: ");
for (int i = 0; i < returnSize; i++) {
printf("%d ", result[i]);
}
printf("\n");
free(result); // 释放结果数组的内存
return 0;
}
迭代法后序遍历
后续遍历代码如下: (注意此时我们和中序遍历相比仅仅改变了两行代码的顺序)
#include <stdio.h>
#include <stdlib.h>
// 定义二叉树节点的结构
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// 定义栈结构
struct Stack {
struct TreeNode* data[100];
int top;
};
// 初始化栈
void initStack(struct Stack* stack) {
stack->top = -1;
}
// 入栈操作
void push(struct Stack* stack, struct TreeNode* node) {
stack->data[++(stack->top)] = node;
}
// 出栈操作
struct TreeNode* pop(struct Stack* stack) {
return stack->data[(stack->top)--];
}
// 判断栈是否为空
int isEmpty(struct Stack* stack) {
return (stack->top == -1);
}
// 后序遍历二叉树的函数
int* postorderTraversal(struct TreeNode* root, int* returnSize) {
int* result = (int*)malloc(100 * sizeof(int)); // 分配大小为 100 的结果数组
int index = 0;
struct TreeNode* prev = NULL;
struct Stack stack;
initStack(&stack);
if (root != NULL) {
push(&stack, root);
}
while (!isEmpty(&stack)) {
struct TreeNode* node = stack.data[stack.top];
if (prev == NULL || prev->left == node || prev->right == node) {
// 当前节点是前一节点的孩子节点或前一节点为空时
if (node->left) {
push(&stack, node->left); // 左子节点入栈
}
else if (node->right) {
push(&stack, node->right); // 右子节点入栈
}
}
else if (node->left == prev) {
// 当前节点是前一节点的左子节点时
if (node->right) {
push(&stack, node->right); // 右子节点入栈
}
}
else {
// 当前节点是前一节点的右子节点或没有孩子节点时,将当前节点的值存入结果数组
result[index++] = node->val;
pop(&stack); // 弹出当前节点
}
prev = node; // 更新前一节点
}
*returnSize = index; // 将结果数组的大小赋给返回的大小指针
return result; // 返回结果数组
}
int main() {
// 创建二叉树节点
// ...
// 进行后序遍历
int returnSize;
int* result = postorderTraversal(root, &returnSize);
// 输出后序遍历的结果
printf("Postorder Traversal: ");
for (int i = 0; i < returnSize; i++) {
printf("%d ", result[i]);
}
printf("\n");
free(result); // 释放结果数组的内存
return 0;
}
102.二叉树的层序遍历
力扣题目链接(opens new window)
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。

思路
我们之前讲过了三篇关于二叉树的深度优先遍历的文章:
二叉树:前中后序递归法(opens new window)
二叉树:前中后序迭代法(opens new window)
二叉树:前中后序迭代方式统一写法(opens new window)
接下来我们再来介绍二叉树的另一种遍历方式:层序遍历。
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。
使用队列实现二叉树广度优先遍历,动画如下:

这样就实现了层序从左到右遍历二叉树。
代码如下:这份代码也可以作为二叉树层序遍历的模板,打十个就靠它了。
#include <stdio.h>
#include <stdlib.h>
// 定义二叉树节点的结构
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// 定义队列结构
struct Queue {
struct TreeNode* data[100];
int front;
int rear;
};
// 初始化队列
void initQueue(struct Queue* queue) {
queue->front = 0;
queue->rear = 0;
}
// 入队操作
void enqueue(struct Queue* queue, struct TreeNode* node) {
queue->data[queue->rear++] = node;
}
// 出队操作
struct TreeNode* dequeue(struct Queue* queue) {
return queue->data[queue->front++];
}
// 判断队列是否为空
int isEmpty(struct Queue* queue) {
return (queue->front == queue->rear);
}
// 二叉树层序遍历的函数
int** levelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes) {
// 分配大小为 100 的结果数组和列数数组
int** result = (int**)malloc(100 * sizeof(int*));
*returnColumnSizes = (int*)malloc(100 * sizeof(int));
*returnSize = 0;
struct Queue queue;
initQueue(&queue);
if (root != NULL) {
enqueue(&queue, root);
}
while (!isEmpty(&queue)) {
int size = queue.rear - queue.front;
int* column = (int*)malloc(size * sizeof(int)); // 分配当前行的列数数组
for (int i = 0; i < size; i++) {
struct TreeNode* node = dequeue(&queue); // 出队节点
column[i] = node->val; // 将节点的值存入列数数组
if (node->left) enqueue(&queue, node->left); // 左子节点入队
if (node->right) enqueue(&queue, node->right); // 右子节点入队
}
result[*returnSize] = column; // 将列数数组存入结果数组
(*returnColumnSizes)[*returnSize] = size; // 存储当前行的列数
(*returnSize)++; // 增加返回的行数
}
return result; // 返回结果数组
}
int main() {
// 创建二叉树节点
// ...
// 进行层序遍历
int returnSize;
int* returnColumnSizes;
int** result = levelOrder(root, &returnSize, &returnColumnSizes);
// 输出层序遍历的结果
printf("Level Order Traversal:\n");
for (int i = 0; i < returnSize; i++) {
printf("Level %d: ", i + 1);
for (int j = 0; j < returnColumnSizes[i]; j++) {
printf("%d ", result[i][j]);
}
printf("\n");
}
// 释放结果数组和列数数组的内存
for (int i = 0; i < returnSize; i++) {
free(result[i]);
}
free(result);
free(returnColumnSizes);
return 0;
}
递归法
#include <stdio.h>
#include <stdlib.h>
// 定义二叉树节点的结构
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// 定义存储结果的动态数组结构
struct DynamicArray {
int* data; // 动态数组的数据
int size; // 动态数组的当前大小
int capacity; // 动态数组的容量
};
// 初始化动态数组
void initDynamicArray(struct DynamicArray* array) {
array->data = (int*)malloc(100 * sizeof(int)); // 初始化容量为100
array->size = 0; // 初始大小为0
array->capacity = 100;
}
// 将元素添加到动态数组
void addToDynamicArray(struct DynamicArray* array, int value) {
if (array->size >= array->capacity) {
// 如果动态数组已满,则扩展数组的容量为原来的两倍
array->capacity *= 2;
array->data = (int*)realloc(array->data, array->capacity * sizeof(int));
}
array->data[array->size++] = value; // 将元素添加到动态数组中,并增加动态数组的大小
}
// 释放动态数组的内存
void freeDynamicArray(struct DynamicArray* array) {
free(array->data); // 释放动态数组的内存空间
}
// 二叉树层序遍历的函数
void levelOrder(struct TreeNode* root, struct DynamicArray* result) {
order(root, result, 0); // 调用递归函数进行二叉树层序遍历
}
// 递归函数,用于层序遍历
void order(struct TreeNode* cur, struct DynamicArray* result, int depth) {
if (cur == NULL) {
return; // 如果当前节点为空,直接返回
}
if (result->size == depth) {
// 如果当前层还未初始化,则为每一层初始化一个动态数组
addToDynamicArray(result, 0);
}
addToDynamicArray(result, cur->val); // 将当前节点的值添加到对应层的动态数组
order(cur->left, result, depth + 1); // 递归遍历左子树
order(cur->right, result, depth + 1); // 递归遍历右子树
}
int main() {
// 创建二叉树节点
// ...
// 进行层序遍历
struct DynamicArray result;
initDynamicArray(&result);
levelOrder(root, &result);
// 输出层序遍历的结果
printf("Level Order Traversal:\n");
for (int i = 0; i < result.size; i++) {
printf("Level %d: ", i);
for (int j = 0; j < result.data[i]; j++) {
printf("%d ", result.data[i * result.capacity + j]);
}
printf("\n");
}
// 释放动态数组的内存
freeDynamicArray(&result);
return 0;
}
107.二叉树的层次遍历 II
力扣题目链接(opens new window)
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)

思路
相对于102.二叉树的层序遍历,就是最后把result数组反转一下就可以了。
#include <stdio.h>
#include <stdlib.h>
// 二叉树节点的结构定义
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// ------------------------------------
// 定义队列结构
struct Queue {
struct TreeNode** array; // 存储二叉树节点指针的数组
int front, rear, size; // 队头、队尾、队列中元素的个数
unsigned capacity; // 队列的容量
};
// 创建一个队列
struct Queue* createQueue(unsigned capacity) {
struct Queue* queue = (struct Queue*)malloc(sizeof(struct Queue));
queue->capacity = capacity;
queue->front = queue->size = 0;
queue->rear = capacity - 1; // 队列为空时,rear设为-1,入队时才会变为0
queue->array = (struct TreeNode**)malloc(queue->capacity * sizeof(struct TreeNode*));
return queue;
}
// 队列是否满
int isFull(struct Queue* queue) {
return (queue->size == queue->capacity);
}
// 队列是否空
int isEmpty(struct Queue* queue) {
return (queue->size == 0);
}
// 入队
void enqueue(struct Queue* queue, struct TreeNode* item) {
if (isFull(queue)) {
return;
}
queue->rear = (queue->rear + 1) % queue->capacity; // 循环队列
queue->array[queue->rear] = item;
queue->size = queue->size + 1;
}
// 出队
struct TreeNode* dequeue(struct Queue* queue) {
if (isEmpty(queue)) {
return NULL;
}
struct TreeNode* item = queue->array[queue->front];
queue->front = (queue->front + 1) % queue->capacity; // 循环队列
queue->size = queue->size - 1;
return item;
}
// ------------------------------------
// 二叉树自底向上的层序遍历
int** levelOrderBottom(struct TreeNode* root, int* returnSize, int** returnColumnSizes) {
*returnSize = 0;
if (root == NULL) {
return NULL;
}
struct Queue* queue = createQueue(100); // 创建队列
struct TreeNode* node;
int capacity = 100;
int** result = (int**)malloc(capacity * sizeof(int*));
*returnColumnSizes = (int*)malloc(capacity * sizeof(int));
// 层序遍历
enqueue(queue, root);
while (!isEmpty(queue)) {
int size = queue->size;
int* currentLevel = (int*)malloc(size * sizeof(int));
(*returnColumnSizes)[*returnSize] = size;
for (int i = 0; i < size; i++) {
node = dequeue(queue);
currentLevel[i] = node->val;
if (node->left) {
enqueue(queue, node->left);
}
if (node->right) {
enqueue(queue, node->right);
}
}
result[*returnSize] = currentLevel;
(*returnSize)++;
if (*returnSize >= capacity) {
capacity *= 2;
result = (int**)realloc(result, capacity * sizeof(int*));
*returnColumnSizes = (int*)realloc(*returnColumnSizes, capacity * sizeof(int));
}
}
// 反转数组
struct TreeNode* tmpNode;
for (int i = 0; i < *returnSize / 2; i++) {
int* tmp = result[i];
result[i] = result[*returnSize - i - 1];
result[*returnSize - i - 1] = tmp;
}
return result;
}
// 测试函数
int main() {
// 创建二叉树节点并进行层序遍历
// ...
return 0;
}
199.二叉树的右视图
力扣题目链接(opens new window)
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。

思路
层序遍历的时候,判断是否遍历到单层的最后面的元素,如果是,就放进result数组中,随后返回result就可以了。
#include <stdio.h>
#include <stdlib.h>
// 二叉树节点的结构定义
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// 定义队列结构
struct Queue {
struct TreeNode** array;
int front, rear, size;
unsigned capacity;
};
// 创建队列
struct Queue* createQueue(unsigned capacity) {
struct Queue* queue = (struct Queue*)malloc(sizeof(struct Queue));
queue->capacity = capacity;
queue->front = queue->size = 0;
queue->rear = capacity - 1;
queue->array = (struct TreeNode**)malloc(queue->capacity * sizeof(struct TreeNode*));
return queue;
}
// 队列是否满
int isFull(struct Queue* queue) {
return (queue->size == queue->capacity);
}
// 队列是否空
int isEmpty(struct Queue* queue) {
return (queue->size == 0);
}
// 入队
void enqueue(struct Queue* queue, struct TreeNode* item) {
if (isFull(queue)) {
return;
}
queue->rear = (queue->rear + 1) % queue->capacity;
queue->array[queue->rear] = item;
queue->size = queue->size + 1;
}
// 出队
struct TreeNode* dequeue(struct Queue* queue) {
if (isEmpty(queue)) {
return NULL;
}
struct TreeNode* item = queue->array[queue->front];
queue->front = (queue->front + 1) % queue->capacity;
queue->size = queue->size - 1;
return item;
}
// 获取二叉树右视图的值
int* rightSideView(struct TreeNode* root, int* returnSize) {
if (root == NULL) {
*returnSize = 0;
return NULL;
}
struct Queue* queue = createQueue(100);
int* result = (int*)malloc(100 * sizeof(int));
int resultSize = 0;
enqueue(queue, root);
while (!isEmpty(queue)) {
int size = queue->size;
for (int i = 0; i < size; i++) {
struct TreeNode* node = dequeue(queue);
if (i == size - 1) {
result[resultSize] = node->val;
resultSize++;
}
if (node->left) {
enqueue(queue, node->left);
}
if (node->right) {
enqueue(queue, node->right);
}
}
}
*returnSize = resultSize;
return result;
}
// 测试函数
int main() {
// 创建二叉树,调用 rightSideView 函数输出结果
return 0;
}
637.二叉树的层平均值
力扣题目链接(opens new window)
给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。

思路
本题就是层序遍历的时候把一层求个总和在取一个均值。
#include <stdio.h>
#include <stdlib.h>
// 二叉树节点的结构定义
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// 定义队列结构
struct Queue {
struct TreeNode** array;
int front, rear, size;
unsigned capacity;
};
// 创建队列
struct Queue* createQueue(unsigned capacity) {
struct Queue* queue = (struct Queue*)malloc(sizeof(struct Queue));
queue->capacity = capacity;
queue->front = queue->size = 0;
queue->rear = capacity - 1;
queue->array = (struct TreeNode**)malloc(queue->capacity * sizeof(struct TreeNode*));
return queue;
}
// 队列是否满
int isFull(struct Queue* queue) {
return (queue->size == queue->capacity);
}
// 队列是否空
int isEmpty(struct Queue* queue) {
return (queue->size == 0);
}
// 入队
void enqueue(struct Queue* queue, struct TreeNode* item) {
if (isFull(queue)) {
return;
}
queue->rear = (queue->rear + 1) % queue->capacity;
queue->array[queue->rear] = item;
queue->size = queue->size + 1;
}
// 出队
struct TreeNode* dequeue(struct Queue* queue) {
if (isEmpty(queue)) {
return NULL;
}
struct TreeNode* item = queue->array[queue->front];
queue->front = (queue->front + 1) % queue->capacity;
queue->size = queue->size - 1;
return item;
}
// 获取二叉树每层平均值的函数
double* averageOfLevels(struct TreeNode* root, int* returnSize) {
if (root == NULL) {
*returnSize = 0;
return NULL;
}
struct Queue* queue = createQueue(100);
double* result = (double*)malloc(100 * sizeof(double));
int resultSize = 0;
enqueue(queue, root);
while (!isEmpty(queue)) {
int size = queue->size;
double sum = 0;
for (int i = 0; i < size; i++) {
struct TreeNode* node = dequeue(queue);
sum += node->val;
if (node->left) {
enqueue(queue, node->left);
}
if (node->right) {
enqueue(queue, node->right);
}
}
result[resultSize] = sum / size;
resultSize++;
}
*returnSize = resultSize;
return result;
}
// 测试函数
int main() {
// 创建二叉树,调用 averageOfLevels 函数输出结果
return 0;
}
429.N叉树的层序遍历
力扣题目链接(opens new window)
给定一个 N 叉树,返回其节点值的层序遍历。 (即从左到右,逐层遍历)。
例如,给定一个 3叉树 :
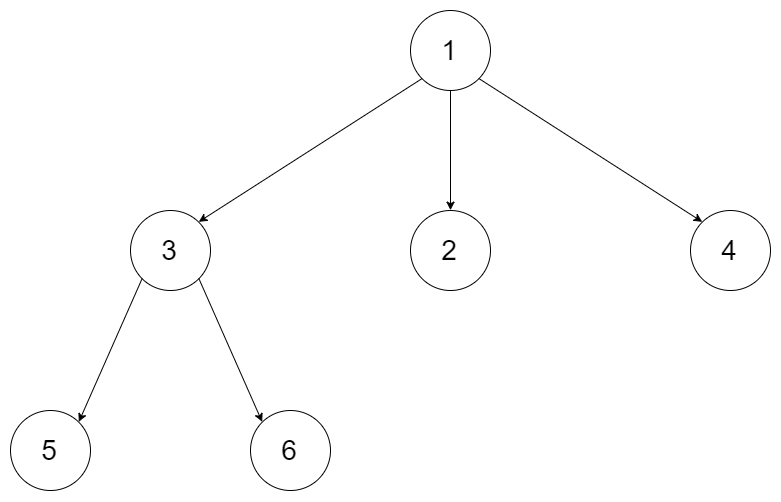
返回其层序遍历:
[ [1], [3,2,4], [5,6] ]
思路
这道题依旧是模板题,只不过一个节点有多个孩子了
#include <stdio.h>
#include <stdlib.h>
// 定义节点结构
struct Node {
int val;
struct Node** children;
int childrenSize;
};
// 定义队列结构
struct Queue {
struct Node** array;
int front, rear, size;
unsigned capacity;
};
// 创建队列
struct Queue* createQueue(unsigned capacity) {
struct Queue* queue = (struct Queue*)malloc(sizeof(struct Queue));
queue->capacity = capacity;
queue->front = 0;
queue->size = 0;
queue->rear = capacity - 1;
queue->array = (struct Node**)malloc(queue->capacity * sizeof(struct Node*));
return queue;
}
// 队列是否满
int isFull(struct Queue* queue) {
return (queue->size == queue->capacity);
}
// 队列是否空
int isEmpty(struct Queue* queue) {
return (queue->size == 0);
}
// 入队
void enqueue(struct Queue* queue, struct Node* item) {
if (isFull(queue)) {
return;
}
queue->rear = (queue->rear + 1) % queue->capacity;
queue->array[queue->rear] = item;
queue->size = queue->size + 1;
}
// 出队
struct Node* dequeue(struct Queue* queue) {
if (isEmpty(queue)) {
return NULL;
}
struct Node* item = queue->array[queue->front];
queue->front = (queue->front + 1) % queue->capacity;
queue->size = queue->size - 1;
return item;
}
// 获取节点的层序遍历结果
int** levelOrder(struct Node* root, int* returnSize, int** returnColumnSizes) {
if (root == NULL) {
*returnSize = 0;
*returnColumnSizes = NULL;
return NULL;
}
struct Queue* queue = createQueue(100);
int** result = (int**)malloc(100 * sizeof(int*));
*returnColumnSizes = (int*)malloc(100 * sizeof(int));
int resultSize = 0;
enqueue(queue, root);
while (!isEmpty(queue)) {
int size = queue->size;
int* column = (int*)malloc(size * sizeof(int));
for (int i = 0; i < size; i++) {
struct Node* node = dequeue(queue);
column[i] = node->val;
for (int j = 0; j < node->childrenSize; j++) {
if (node->children[j]) {
enqueue(queue, node->children[j]);
}
}
}
result[resultSize] = column;
(*returnColumnSizes)[resultSize] = size;
resultSize++;
}
*returnSize = resultSize;
return result;
}
// 测试函数
int main() {
// 创建树节点,调用 levelOrder 函数输出结果
return 0;
}
515.在每个树行中找最大值
力扣题目链接(opens new window)
您需要在二叉树的每一行中找到最大的值。
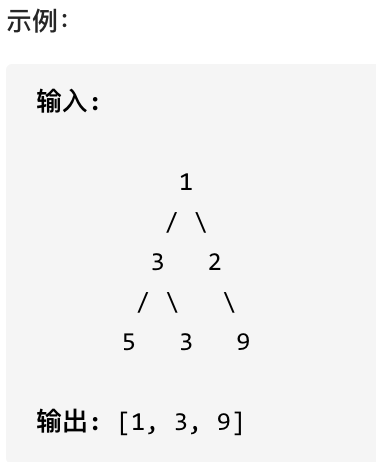
思路
层序遍历,取每一层的最大值
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
// 定义树节点结构
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// 定义队列结构
struct Queue {
struct TreeNode** array; // 存储树节点的数组
int front, rear, size; // 队列的前端、后端索引以及当前大小
unsigned capacity; // 队列的容量
};
// 创建队列
struct Queue* createQueue(unsigned capacity) {
struct Queue* queue = (struct Queue*)malloc(sizeof(struct Queue));
queue->capacity = capacity;
queue->front = 0;
queue->size = 0;
queue->rear = capacity - 1;
queue->array = (struct TreeNode**)malloc(queue->capacity * sizeof(struct TreeNode*));
return queue;
}
// 队列是否满
int isFull(struct Queue* queue) {
return (queue->size == queue->capacity);
}
// 队列是否空
int isEmpty(struct Queue* queue) {
return (queue->size == 0);
}
// 入队
void enqueue(struct Queue* queue, struct TreeNode* item) {
if (isFull(queue)) {
return;
}
queue->rear = (queue->rear + 1) % queue->capacity; // 更新后端索引
queue->array[queue->rear] = item; // 将节点放入后端
queue->size = queue->size + 1; // 更新队列大小
}
// 出队
struct TreeNode* dequeue(struct Queue* queue) {
if (isEmpty(queue)) {
return NULL;
}
struct TreeNode* item = queue->array[queue->front]; // 获取前端节点
queue->front = (queue->front + 1) % queue->capacity; // 更新前端索引
queue->size = queue->size - 1; // 更新队列大小
return item;
}
// 获取每层最大值的数组
int* largestValues(struct TreeNode* root, int* returnSize) {
if (root == NULL) {
*returnSize = 0;
return NULL;
}
struct Queue* queue = createQueue(100); // 创建队列
int* result = (int*)malloc(100 * sizeof(int)); // 创建存储结果的数组
*returnSize = 0;
enqueue(queue, root); // 根节点入队
while (!isEmpty(queue)) {
int size = queue->size; // 当前层的节点数
int maxValue = INT_MIN; // 当前层的最大值
for (int i = 0; i < size; i++) {
struct TreeNode* node = dequeue(queue); // 出队
maxValue = node->val > maxValue ? node->val : maxValue; // 更新最大值
if (node->left) {
enqueue(queue, node->left); // 左子节点入队
}
if (node->right) {
enqueue(queue, node->right); // 右子节点入队
}
}
result[*returnSize] = maxValue; // 将最大值放入结果数组
(*returnSize)++; // 更新结果数组大小
}
return result;
}
// 测试函数
int main() {
// 创建树节点,调用 largestValues 函数输出结果
return 0;
}
16.填充每个节点的下一个右侧节点指针
力扣题目链接(opens new window)
给定一个完美二叉树,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
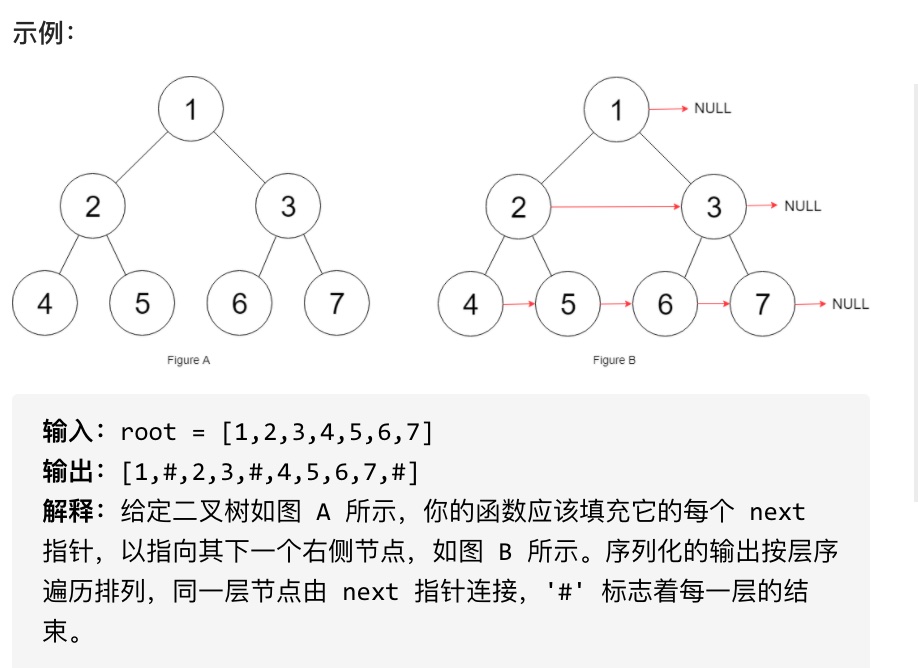
思路
本题依然是层序遍历,只不过在单层遍历的时候记录一下本层的头部节点,然后在遍历的时候让前一个节点指向本节点就可以了
#include <stdio.h>
#include <stdlib.h>
// 定义节点结构体
struct Node {
int val;
struct Node* left;
struct Node* right;
struct Node* next; // 指向同一层的下一个节点
};
// 定义队列结构体
struct Queue {
struct Node** array; // 存储节点的数组
int front, rear, size; // 队列的前端、后端索引以及当前大小
unsigned capacity; // 队列的容量
};
// 创建一个新的队列
struct Queue* createQueue(unsigned capacity) {
struct Queue* queue = (struct Queue*)malloc(sizeof(struct Queue)); // 分配内存
queue->capacity = capacity;
queue->front = 0;
queue->size = 0;
queue->rear = capacity - 1;
queue->array = (struct Node**)malloc(queue->capacity * sizeof(struct Node*)); // 使用数组存储节点
return queue;
}
// 检查队列是否已满
int isFull(struct Queue* queue) {
return (queue->size == queue->capacity);
}
// 检查队列是否为空
int isEmpty(struct Queue* queue) {
return (queue->size == 0);
}
// 入队操作
void enqueue(struct Queue* queue, struct Node* item) {
if (isFull(queue)) {
return; // 队列已满时返回
}
queue->rear = (queue->rear + 1) % queue->capacity; // 后端索引加一
queue->array[queue->rear] = item; // 在新的后端索引处存储节点
queue->size = queue->size + 1; // 队列大小加一
}
// 出队操作
struct Node* dequeue(struct Queue* queue) {
if (isEmpty(queue)) {
return NULL; // 队列为空时返回空指针
}
struct Node* item = queue->array[queue->front]; // 取出前端节点
queue->front = (queue->front + 1) % queue->capacity; // 前端索引加一
queue->size = queue->size - 1; // 队列大小减一
return item; // 返回取出的节点
}
// 连接同一层的节点
struct Node* connect(struct Node* root) {
struct Queue* que = createQueue(100); // 创建存储节点的队列
if (root != NULL) {
enqueue(que, root); // 将根节点入队
}
while (!isEmpty(que)) {
int size = que->size;
struct Node* nodePre;
struct Node* node;
for (int i = 0; i < size; i++) {
if (i == 0) {
nodePre = dequeue(que); // 取出一层的头结点
node = nodePre;
} else {
node = dequeue(que);
nodePre->next = node; // 本层前一个节点next指向本节点
nodePre = nodePre->next;
}
if (node->left) {
enqueue(que, node->left); // 将左子节点入队
}
if (node->right) {
enqueue(que, node->right); // 将右子节点入队
}
}
nodePre->next = NULL; // 本层最后一个节点指向NULL
}
return root; // 返回根节点
}
int main() {
// 创建测试用例并调用connect函数进行连接操作
// 输出结果
return 0;
}
117.填充每个节点的下一个右侧节点指针II
力扣题目链接(opens new window)
思路
这道题目说是二叉树,但116题目说是完整二叉树,其实没有任何差别,一样的代码一样的逻辑一样的味道
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
while (!que.empty()) {
int size = que.size();
vector<int> vec;
Node* nodePre;
Node* node;
for (int i = 0; i < size; i++) {
if (i == 0) {
nodePre = que.front(); // 取出一层的头结点
que.pop();
node = nodePre;
} else {
node = que.front();
que.pop();
nodePre->next = node; // 本层前一个节点next指向本节点
nodePre = nodePre->next;
}
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
nodePre->next = NULL; // 本层最后一个节点指向NULL
}
return root;
}
104.二叉树的最大深度
力扣题目链接(opens new window)
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],

返回它的最大深度 3 。
思路
使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
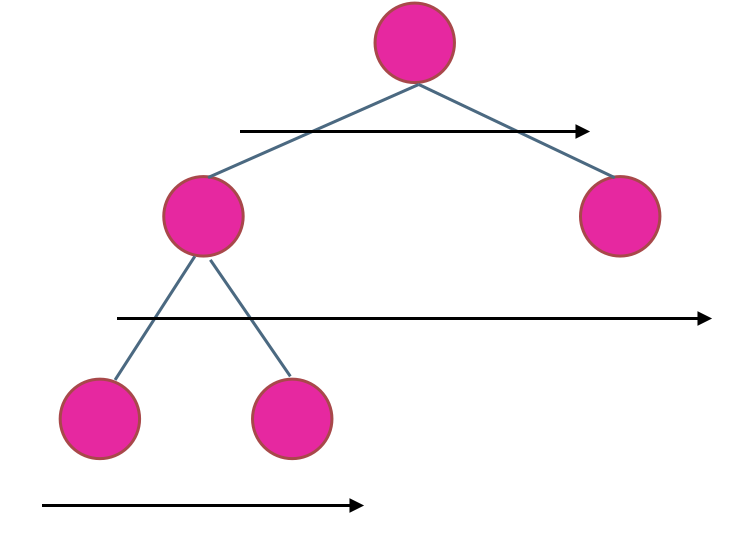
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
};
struct Queue {
struct TreeNode **array; // 用于存储节点的数组
int front, rear, size; // 队列的前端、后端索引以及当前大小
unsigned capacity; // 队列的容量
};
struct Queue *createQueue(unsigned capacity) {
struct Queue *queue = (struct Queue *)malloc(sizeof(struct Queue)); // 分配队列内存
queue->capacity = capacity;
queue->front = 0;
queue->size = 0;
queue->rear = capacity - 1;
queue->array = (struct TreeNode **)malloc(queue->capacity * sizeof(struct TreeNode *)); // 使用数组存储节点
return queue;
}
int isFull(struct Queue *queue) {
return (queue->size == queue->capacity);
}
int isEmpty(struct Queue *queue) {
return (queue->size == 0);
}
void enqueue(struct Queue *queue, struct TreeNode *item) {
if (isFull(queue)) {
return; // 队列已满时返回
}
queue->rear = (queue->rear + 1) % queue->capacity; // 后端索引加一
queue->array[queue->rear] = item; // 在新的后端索引处存储节点
queue->size = queue->size + 1; // 队列大小加一
}
struct TreeNode *dequeue(struct Queue *queue) {
if (isEmpty(queue)) {
return NULL; // 队列为空时返回空指针
}
struct TreeNode* item = queue->array[queue->front]; // 取出前端节点
queue->front = (queue->front + 1) % queue->capacity; // 前端索引加一
queue->size = queue->size - 1; // 队列大小减一
return item; // 返回取出的节点
}
int maxDepth(struct TreeNode* root) {
if (root == NULL) return 0;
int depth = 0;
struct Queue* que = createQueue(100); // 创建存储节点的队列
enqueue(que, root);
while (!isEmpty(que)) {
int size = que->size;
depth++; // 记录深度
for (int i = 0; i < size; i++) {
struct TreeNode* node = dequeue(que);
if (node->left) enqueue(que, node->left);
if (node->right) enqueue(que, node->right);
}
}
return depth;
}
111.二叉树的最小深度
力扣题目链接(opens new window)
思路
相对于 104.二叉树的最大深度 ,本题还也可以使用层序遍历的方式来解决,思路是一样的。
需要注意的是,只有当左右孩子都为空的时候,才说明遍历的最低点了。如果其中一个孩子为空则不是最低点
代码如下:(详细注释)
int minDepth(struct TreeNode* root) {
if (root == NULL) return 0;
int depth = 0;
struct Queue* que = createQueue(100); // 创建存储节点的队列
enqueue(que, root);
while (!isEmpty(que)) {
int size = que->size;
depth++; // 记录最小深度
for (int i = 0; i < size; i++) {
struct TreeNode* node = dequeue(que);
if (node->left) enqueue(que, node->left);
if (node->right) enqueue(que, node->right);
if (!node->left && !node->right) { // 当左右孩子都为空的时候,说明是最低点的一层了,退出
return depth;
}
}
}
return depth;
}
总结
二叉树的层序遍历,就是图论中的广度优先搜索在二叉树中的应用,需要借助队列来实现(此时又发现队列的一个应用了)。
来吧,一口气打十个:
- 102.二叉树的层序遍历(opens new window)
- 107.二叉树的层次遍历II(opens new window)
- 199.二叉树的右视图(opens new window)
- 637.二叉树的层平均值(opens new window)
- 429.N叉树的层序遍历(opens new window)
- 515.在每个树行中找最大值(opens new window)
- 116.填充每个节点的下一个右侧节点指针(opens new window)
- 117.填充每个节点的下一个右侧节点指针II(opens new window)
- 104.二叉树的最大深度(opens new window)
- 111.二叉树的最小深度(opens new window)
致敬叶师傅!
226.翻转二叉树
力扣题目链接(opens new window)
翻转一棵二叉树。
这道题目背后有一个让程序员心酸的故事,听说 Homebrew的作者Max Howell,就是因为没在白板上写出翻转二叉树,最后被Google拒绝了。(真假不做判断,权当一个乐子哈)
题外话
这道题目是非常经典的题目,也是比较简单的题目(至少一看就会)。
但正是因为这道题太简单,一看就会,一些同学都没有抓住起本质,稀里糊涂的就把这道题目过了。
如果做过这道题的同学也建议认真看完,相信一定有所收获!
思路
我们之前介绍的都是各种方式遍历二叉树,这次要翻转了,感觉还是有点懵逼。
这得怎么翻转呢?
如果要从整个树来看,翻转还真的挺复杂,整个树以中间分割线进行翻转,如图:
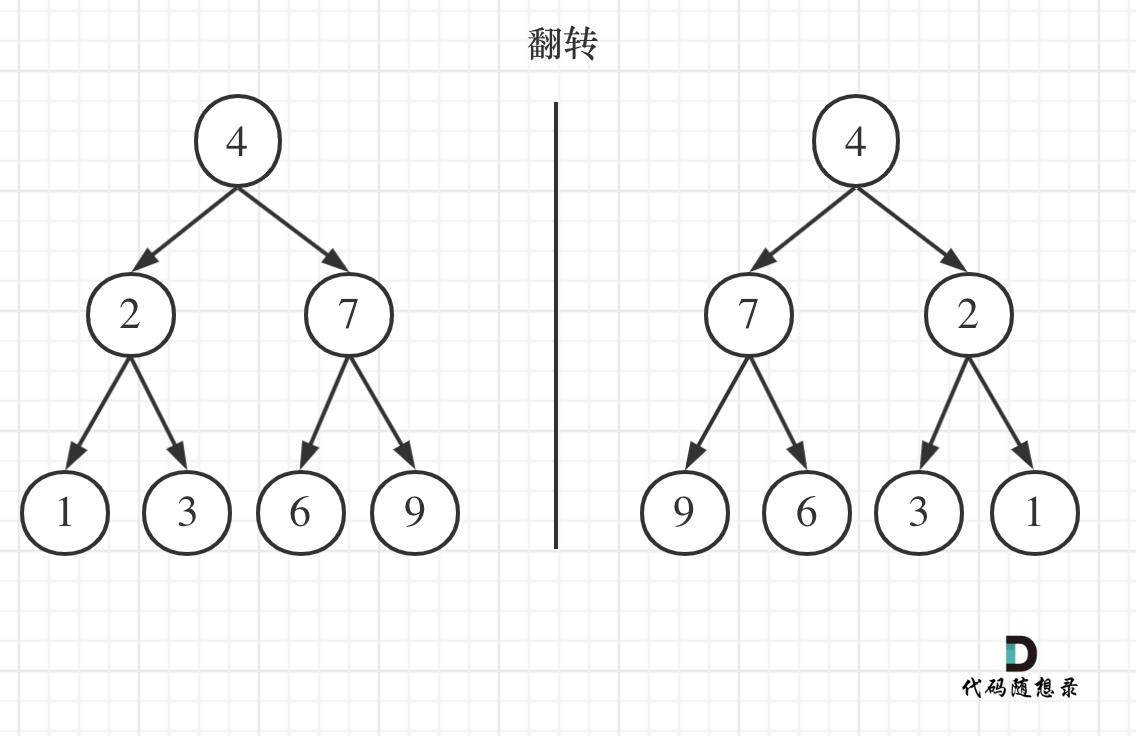
可以发现想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
关键在于遍历顺序,前中后序应该选哪一种遍历顺序? (一些同学这道题都过了,但是不知道自己用的是什么顺序)
遍历的过程中去翻转每一个节点的左右孩子就可以达到整体翻转的效果。
注意只要把每一个节点的左右孩子翻转一下,就可以达到整体翻转的效果
这道题目使用前序遍历和后序遍历都可以,唯独中序遍历不方便,因为中序遍历会把某些节点的左右孩子翻转了两次!建议拿纸画一画,就理解了
那么层序遍历可以不可以呢?依然可以的!只要把每一个节点的左右孩子翻转一下的遍历方式都是可以的!
递归法
对于二叉树的递归法的前中后序遍历,已经在二叉树:前中后序递归遍历 (opens new window)详细讲解了。
我们下文以前序遍历为例,通过动画来看一下翻转的过程:

我们来看一下递归三部曲:
确定递归函数的参数和返回值
参数就是要传入节点的指针,不需要其他参数了,通常此时定下来主要参数,如果在写递归的逻辑中发现还需要其他参数的时候,随时补充。
返回值的话其实也不需要,但是题目中给出的要返回root节点的指针,可以直接使用题目定义好的函数,所以就函数的返回类型为TreeNode*。
TreeNode* invertTree(TreeNode* root)
确定终止条件
当前节点为空的时候,就返回
if (root == NULL) return root;
确定单层递归的逻辑
因为是先前序遍历,所以先进行交换左右孩子节点,然后反转左子树,反转右子树。
swap(root->left, root->right);
invertTree(root->left);
invertTree(root->right);
基于这递归三步法,代码基本写完
struct TreeNode* invertTree(struct TreeNode* root) {
if (root == NULL) return root;
struct TreeNode* temp = root->left;
root->left = root->right;
root->right = temp;
invertTree(root->left);
invertTree(root->right);
return root;
}
迭代法
深度优先遍历
二叉树:听说递归能做的,栈也能做! (opens new window)中给出了前中后序迭代方式的写法,所以本题可以很轻松的写出如下迭代法的代码:
struct TreeNode* invertTree(struct TreeNode* root) {
if (root == NULL) return root;
struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*)*1000); // 创建一个栈用于存储节点指针
int top = -1; // 栈顶指针初始化为-1,表示栈为空
stack[++top] = root; // 将根节点入栈
while (top > -1) { // 当栈不为空时,循环执行下面的代码
struct TreeNode* node = stack[top]; // 取出栈顶元素作为当前节点
top--; // 栈顶指针下移,相当于出栈操作
// 交换当前节点的左右子节点
struct TreeNode* temp = node->left;
node->left = node->right;
node->right = temp;
// 将右子节点入栈,注意先入右子节点再入左子节点,保证左子节点后出栈
if (node->right) stack[++top] = node->right;
if (node->left) stack[++top] = node->left;
}
free(stack); // 释放栈的内存空间
return root; // 返回反转后的根节点
}
如果这个代码看不懂的话可以再回顾一下二叉树:听说递归能做的,栈也能做! (opens new window)。
我们在二叉树:前中后序迭代方式的统一写法 (opens new window)中介绍了统一的写法,所以,本题也只需将文中的代码少做修改便可。
struct TreeNode* invertTree(struct TreeNode* root) {
struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 1000); // 创建一个栈用于存储节点指针
int top = -1; // 栈顶指针初始化为-1,表示栈为空
if (root != NULL) {
stack[++top] = root; // 根节点入栈
}
while (top > -1) { // 当栈不为空时,循环执行下面的代码
struct TreeNode* node = stack[top]; // 取出栈顶元素
if (node != NULL) {
stack.pop();
if (node->right) stack[++top] = node->right; // 右子节点入栈
if (node->left) stack[++top] = node->left; // 左子节点入栈
stack[++top] = node; // 当前节点入栈
stack[++top] = NULL; // NULL标记入栈,用于表示当前节点已经处理过
} else {
stack[top--]; // 弹出NULL标记
node = stack[top]; // 取出当前节点
stack[top--]; // 弹出当前节点
// 交换当前节点的左右子节点
struct TreeNode* temp = node->left;
node->left = node->right;
node->right = temp;
}
}
free(stack); // 释放栈的内存空间
return root; // 返回反转后的根节点
}
如果上面这个代码看不懂,回顾一下文章二叉树:前中后序迭代方式的统一写法 (opens new window)。
广度优先遍历
也就是层序遍历,层数遍历也是可以翻转这棵树的,因为层序遍历也可以把每个节点的左右孩子都翻转一遍,代码如下:
struct TreeNode* invertTree(struct TreeNode* root) {
struct TreeNode** queue = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 1000); // 创建一个队列用于存储节点指针
int front = 0; // 队首指针
int rear = 0; // 队尾指针
if (root != NULL) {
queue[rear++] = root; // 根节点入队
}
while (front != rear) { // 当队列不为空时,循环执行下面的代码
int size = rear - front; // 当前队列中的节点数
for (int i = 0; i < size; i++) {
struct TreeNode* node = queue[front++]; // 取出队首元素
// 交换当前节点的左右子节点
struct TreeNode* temp = node->left;
node->left = node->right;
node->right = temp;
// 左右子节点入队
if (node->left) queue[rear++] = node->left;
if (node->right) queue[rear++] = node->right;
}
}
free(queue); // 释放队列的内存空间
return root; // 返回反转后的根节点
}
如果对以上代码不理解,或者不清楚二叉树的层序遍历,可以看这篇二叉树:层序遍历登场!
总结
针对二叉树的问题,解题之前一定要想清楚究竟是前中后序遍历,还是层序遍历。
二叉树解题的大忌就是自己稀里糊涂的过了(因为这道题相对简单),但是也不知道自己是怎么遍历的。
这也是造成了二叉树的题目“一看就会,一写就废”的原因。
针对翻转二叉树,我给出了一种递归,三种迭代(两种模拟深度优先遍历,一种层序遍历)的写法,都是之前我们讲过的写法,融汇贯通一下而已。
大家一定也有自己的解法,但一定要成方法论,这样才能通用,才能举一反三!
101. 对称二叉树
力扣题目链接(opens new window)
给定一个二叉树,检查它是否是镜像对称的。

思路
首先想清楚,判断对称二叉树要比较的是哪两个节点,要比较的可不是左右节点!
对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了其实我们要比较的是两个树(这两个树是根节点的左右子树),所以在递归遍历的过程中,也是要同时遍历两棵树。
那么如何比较呢?
比较的是两个子树的里侧和外侧的元素是否相等。如图所示:
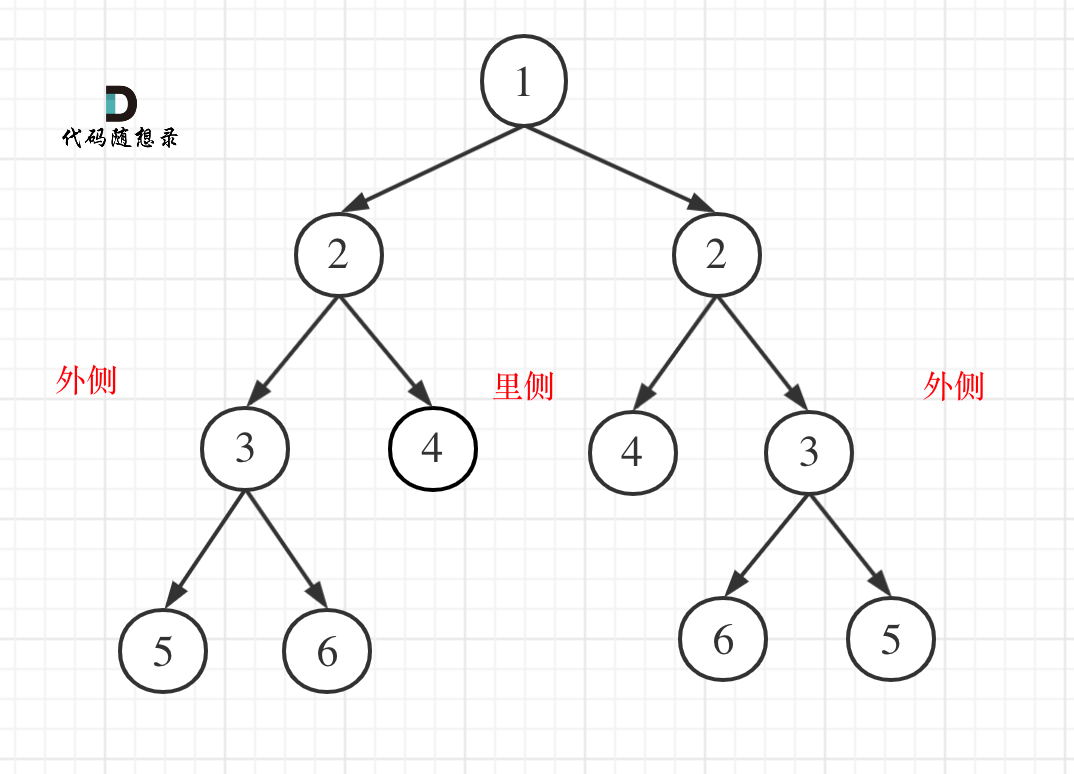
那么遍历的顺序应该是什么样的呢?
本题遍历只能是“后序遍历”,因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。
正是因为要遍历两棵树而且要比较内侧和外侧节点,所以准确的来说是一个树的遍历顺序是左右中,一个树的遍历顺序是右左中。
但都可以理解算是后序遍历,尽管已经不是严格上在一个树上进行遍历的后序遍历了。
其实后序也可以理解为是一种回溯,当然这是题外话,讲回溯的时候会重点讲的。
说到这大家可能感觉我有点啰嗦,哪有这么多道理,上来就干就完事了。别急,我说的这些在下面的代码讲解中都有身影。
那么我们先来看看递归法的代码应该怎么写。
递归法
递归三部曲
确定递归函数的参数和返回值
因为我们要比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。
返回值自然是bool类型。
代码如下:
bool compare(TreeNode* left, TreeNode* right)
确定终止条件
要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。
节点为空的情况有:(注意我们比较的其实不是左孩子和右孩子,所以如下我称之为左节点右节点)
左节点为空,右节点不为空,不对称,return false
左不为空,右为空,不对称 return false
左右都为空,对称,返回true
此时已经排除掉了节点为空的情况,那么剩下的就是左右节点不为空:
左右都不为空,比较节点数值,不相同就return false
此时左右节点不为空,且数值也不相同的情况我们也处理了。
代码如下:
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里我没有使用else
注意上面最后一种情况,我没有使用else,而是else if, 因为我们把以上情况都排除之后,剩下的就是 左右节点都不为空,且数值相同的情况。
确定单层递归的逻辑
此时才进入单层递归的逻辑,单层递归的逻辑就是处理 左右节点都不为空,且数值相同的情况。
比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
比较内侧是否对称,传入左节点的右孩子,右节点的左孩子。
如果左右都对称就返回true ,有一侧不对称就返回false 。
代码如下:
bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
bool inside = compare(left->right, right->left);// 左子树:右、 右子树:左
bool isSame = outside && inside;// 左子树:中、 右子树:中(逻辑处理)
return isSame;
如上代码中,我们可以看出使用的遍历方式,左子树左右中,右子树右左中,所以我把这个遍历顺序也称之为“后序遍历”(尽管不是严格的后序遍历)。
最后递归的C++整体代码如下:
bool compare(TreeNode* left, TreeNode* right) {
// 首先排除空节点的情况
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
// 排除了空节点,再排除数值不相同的情况
else if (left->val != right->val) return false;
// 此时就是:左右节点都不为空,且数值相同的情况
// 此时才做递归,做下一层的判断
bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
bool inside = compare(left->right, right->left);// 左子树:右、 右子树:左
bool isSame = outside && inside;// 左子树:中、 右子树:中 (逻辑处理)
return isSame;
}
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
return compare(root->left, root->right);
}
我给出的代码并不简洁,但是把每一步判断的逻辑都清楚的描绘出来了。
如果上来就看网上各种简洁的代码,看起来真的很简单,但是很多逻辑都掩盖掉了,而题解可能也没有把掩盖掉的逻辑说清楚。
盲目的照着抄,结果就是:发现这是一道“简单题”,稀里糊涂的就过了,但是真正的每一步判断逻辑未必想到清楚。
当然我可以把如上代码整理如下:
bool compare(TreeNode* left, TreeNode* right) {
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false;
else return compare(left->left, right->right) && compare(left->right, right->left);
}
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
return compare(root->left, root->right);
}
这个代码就很简洁了,但隐藏了很多逻辑,条理不清晰,而且递归三部曲,在这里完全体现不出来。
所以建议大家做题的时候,一定要想清楚逻辑,每一步做什么。把题目所有情况想到位,相应的代码写出来之后,再去追求简洁代码的效果。
迭代法
这道题目我们也可以使用迭代法,但要注意,这里的迭代法可不是前中后序的迭代写法,因为本题的本质是判断两个树是否是相互翻转的,其实已经不是所谓二叉树遍历的前中后序的关系了。
这里我们可以使用队列来比较两个树(根节点的左右子树)是否相互翻转,(注意这不是层序遍历)
使用队列
通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等,如动画所示:

如下的条件判断和递归的逻辑是一样的。
代码如下:
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
queue<TreeNode*> que;
que.push(root->left); // 将左子树头结点加入队列
que.push(root->right); // 将右子树头结点加入队列
while (!que.empty()) { // 接下来就要判断这两个树是否相互翻转
TreeNode* leftNode = que.front(); que.pop();
TreeNode* rightNode = que.front(); que.pop();
if (!leftNode && !rightNode) { // 左节点为空、右节点为空,此时说明是对称的
continue;
}
// 左右一个节点不为空,或者都不为空但数值不相同,返回false
if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
return false;
}
que.push(leftNode->left); // 加入左节点左孩子
que.push(rightNode->right); // 加入右节点右孩子
que.push(leftNode->right); // 加入左节点右孩子
que.push(rightNode->left); // 加入右节点左孩子
}
return true;
}
使用栈
细心的话,其实可以发现,这个迭代法,其实是把左右两个子树要比较的元素顺序放进一个容器,然后成对成对的取出来进行比较,那么其实使用栈也是可以的。
只要把队列原封不动的改成栈就可以了,我下面也给出了代码。
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
stack<TreeNode*> st; // 这里改成了栈
st.push(root->left);
st.push(root->right);
while (!st.empty()) {
TreeNode* leftNode = st.top(); st.pop();
TreeNode* rightNode = st.top(); st.pop();
if (!leftNode && !rightNode) {
continue;
}
if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
return false;
}
st.push(leftNode->left);
st.push(rightNode->right);
st.push(leftNode->right);
st.push(rightNode->left);
}
return true;
}
总结
这次我们又深度剖析了一道二叉树的“简单题”,大家会发现,真正的把题目搞清楚其实并不简单,leetcode上accept了和真正掌握了还是有距离的。
我们介绍了递归法和迭代法,递归依然通过递归三部曲来解决了这道题目,如果只看精简的代码根本看不出来递归三部曲是如何解题的。
在迭代法中我们使用了队列,需要注意的是这不是层序遍历,而且仅仅通过一个容器来成对的存放我们要比较的元素,知道这一本质之后就发现,用队列,用栈,甚至用数组,都是可以的。
如果已经做过这道题目的同学,读完文章可以再去看看这道题目,思考一下,会有不一样的发现!
相关题目推荐
这两道题目基本和本题是一样的,只要稍加修改就可以AC。
100.相同的树(opens new window)
572.另一个树的子树
222.完全二叉树的节点个数
力扣题目链接(opens new window)
给出一个完全二叉树,求出该树的节点个数。
示例 1:
输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1
提示:
树中节点的数目范围是[0, 5 * 10^4]
0 <= Node.val <= 5 * 10^4
题目数据保证输入的树是 完全二叉树
思路
本篇给出按照普通二叉树的求法以及利用完全二叉树性质的求法。
普通二叉树
首先按照普通二叉树的逻辑来求。
这道题目的递归法和求二叉树的深度写法类似, 而迭代法,二叉树:层序遍历登场! (opens new window)遍历模板稍稍修改一下,记录遍历的节点数量就可以了。
递归遍历的顺序依然是后序(左右中)。
递归
如果对求二叉树深度还不熟悉的话,看这篇:二叉树:看看这些树的最大深度 (opens new window)。
确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回以该节点为根节点二叉树的节点数量,所以返回值为int类型。
代码如下:
int getNodesNum(TreeNode* cur) {
确定终止条件:如果为空节点的话,就返回0,表示节点数为0。
代码如下:
if (cur == NULL) return 0;
确定单层递归的逻辑:先求它的左子树的节点数量,再求右子树的节点数量,最后取总和再加一 (加1是因为算上当前中间节点)就是目前节点为根节点的节点数量。
代码如下:
int leftNum = getNodesNum(cur->left); // 左
int rightNum = getNodesNum(cur->right); // 右
int treeNum = leftNum + rightNum + 1; // 中
return treeNum;
所以整体C++代码如下:
//版本一
int getNodesNum(TreeNode* cur) {
if (cur == NULL) return 0;
int leftNum = getNodesNum(cur->left); // 左
int rightNum = getNodesNum(cur->right);// 右
int treeNum = leftNum + rightNum + 1; // 中
return treeNum;
}
int countNodes(TreeNode* root) {
return getNodesNum(root);
}
//版本二
int countNodes(TreeNode* root) {
if (root == NULL) return 0;
return 1 + countNodes(root->left) + countNodes(root->right);
}
网上基本都是这个精简的代码版本,其实不建议大家照着这个来写,代码确实精简,但隐藏了一些内容,连遍历的顺序都看不出来,所以初学者建议学习版本一的代码,稳稳的打基础。
迭代
如果对求二叉树层序遍历还不熟悉的话,看这篇:二叉树:层序遍历登场! (opens new window)。
那么只要模板少做改动,加一个变量result,统计节点数量就可以了
int countNodes(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
int result = 0;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
result++; // 记录节点数量
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return result;
}
完全二叉树
以上方法都是按照普通二叉树来做的,对于完全二叉树特性不了解的同学可以看这篇 关于二叉树,你该了解这些! (opens new window),这篇详细介绍了各种二叉树的特性。
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。
大家要自己看完全二叉树的定义,很多同学对完全二叉树其实不是真正的懂了。
我来举一个典型的例子如题:
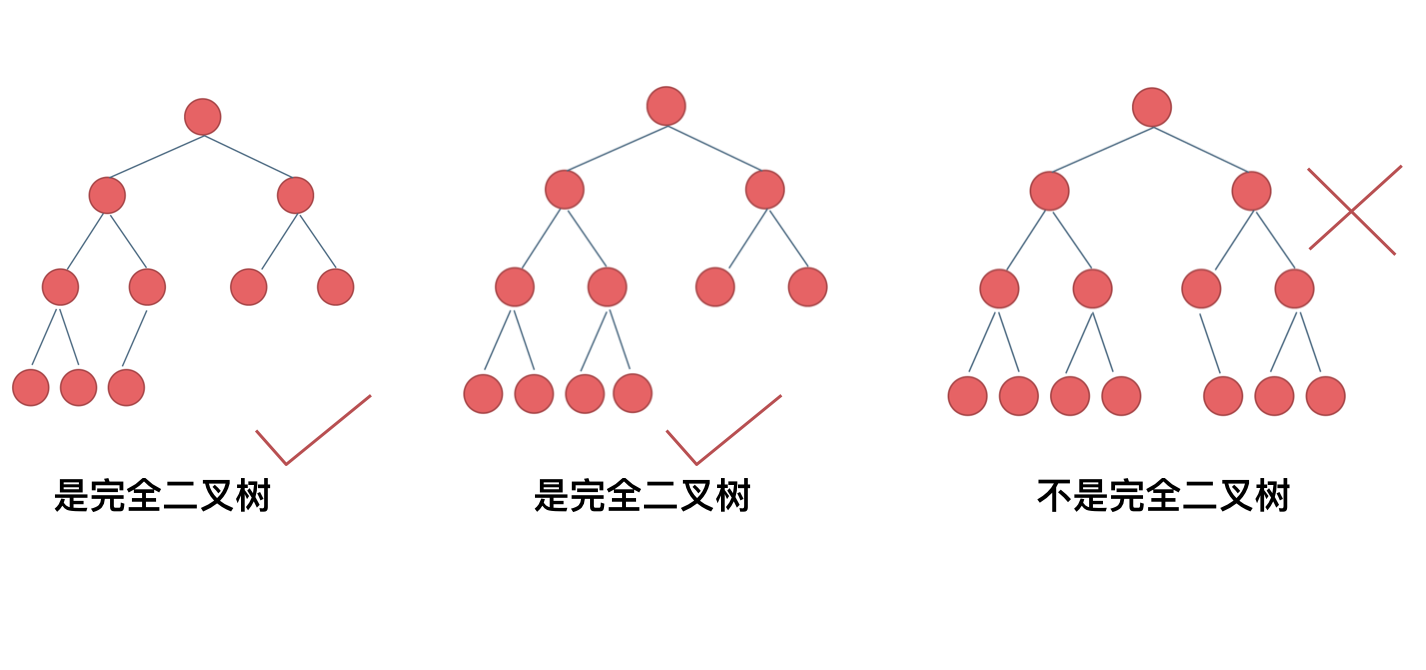
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
完全二叉树(一)如图:
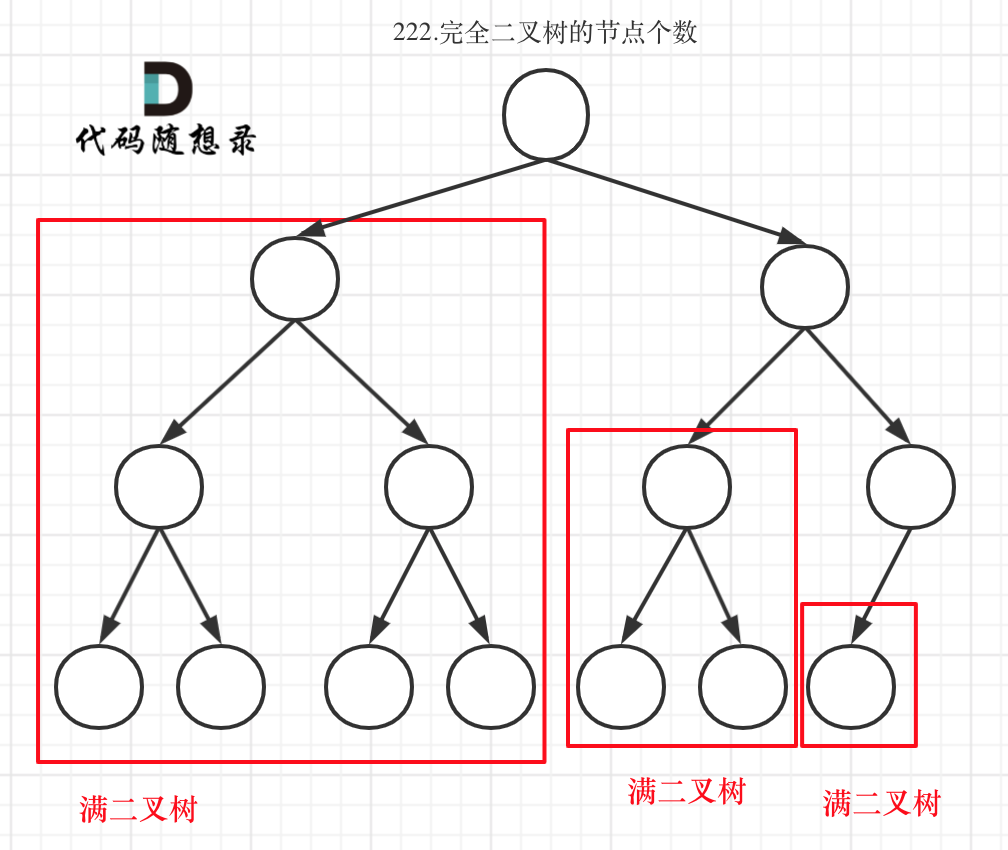
完全二叉树(二)如图:
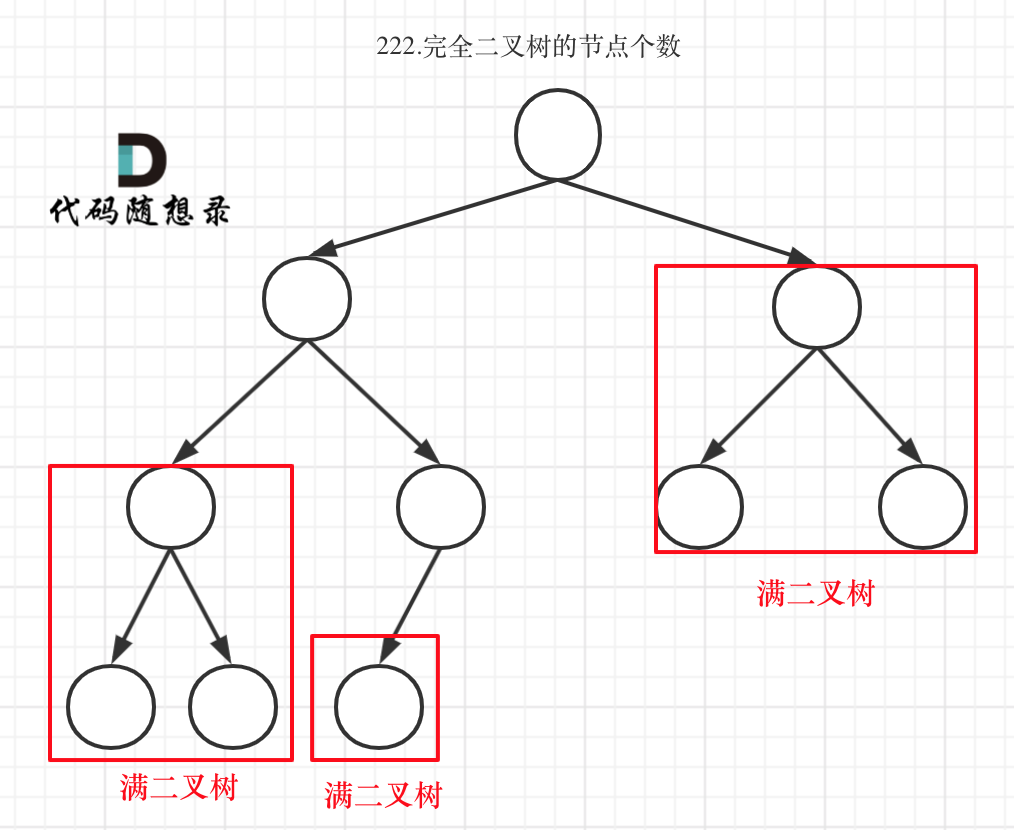
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢?
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。如图:
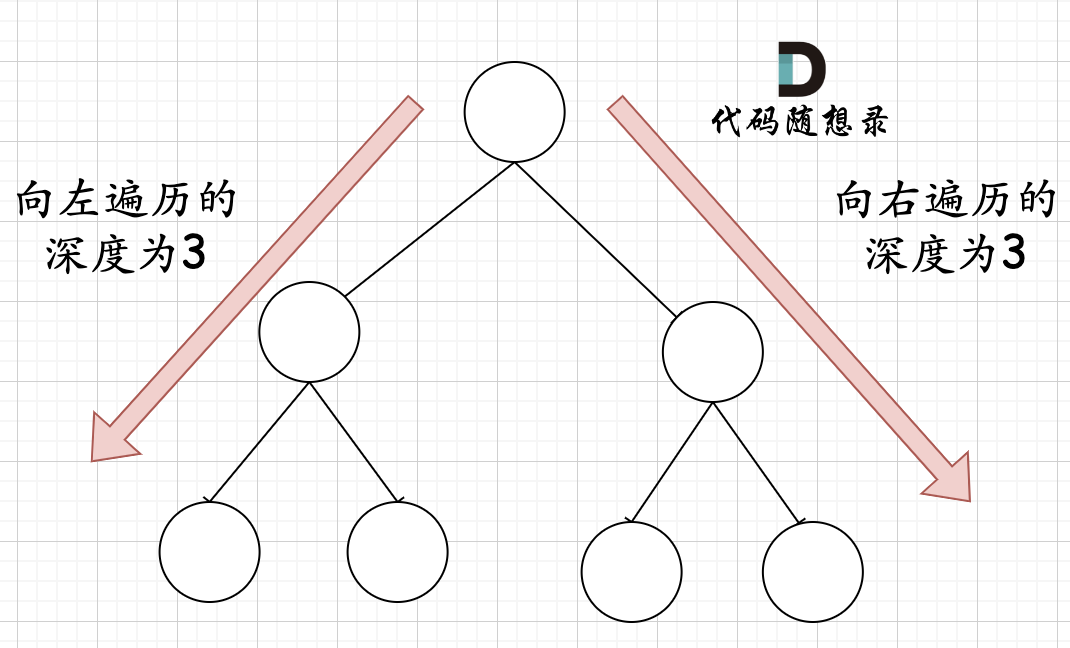
在完全二叉树中,如果递归向左遍历的深度不等于递归向右遍历的深度,则说明不是满二叉树,如图:
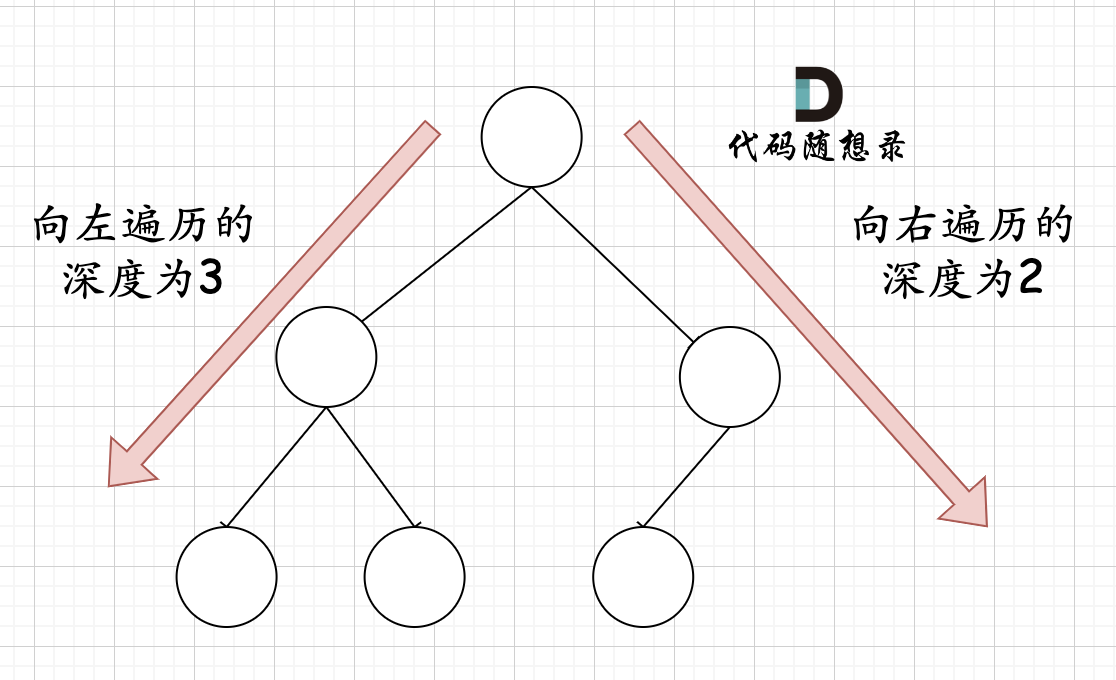
那有录友说了,这种情况,递归向左遍历的深度等于递归向右遍历的深度,但也不是满二叉树,如题:
如果这么想,大家就是对 完全二叉树理解有误区了,以上这棵二叉树,它根本就不是一个完全二叉树!
判断其子树是不是满二叉树,如果是则利用公式计算这个子树(满二叉树)的节点数量,如果不是则继续递归,那么 在递归三部曲中,第二部:终止条件的写法应该是这样的:
if (root == nullptr) return 0;
// 开始根据左深度和右深度是否相同来判断该子树是不是满二叉树
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的,为了下面求指数方便
while (left) { // 求左子树深度
left = left->left;
leftDepth++;
}
while (right) { // 求右子树深度
right = right->right;
rightDepth++;
}
if (leftDepth == rightDepth) {
return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2,返回满足满二叉树的子树节点数量
}
递归三部曲,第三部,单层递归的逻辑:(可以看出使用后序遍历)
int leftTreeNum = countNodes(root->left); // 左
int rightTreeNum = countNodes(root->right); // 右
int result = leftTreeNum + rightTreeNum + 1;// 中
return result;
该部分精简之后代码为:
return countNodes(root->left) + countNodes(root->right) + 1;
最后整体C++代码如下:
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == nullptr) return 0;
TreeNode* left = root->left;
TreeNode* right = root->right;
int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的,为了下面求指数方便
while (left) { // 求左子树深度
left = left->left;
leftDepth++;
}
while (right) { // 求右子树深度
right = right->right;
rightDepth++;
}
if (leftDepth == rightDepth) {
return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2,所以leftDepth初始为0
}
return countNodes(root->left) + countNodes(root->right) + 1;
}
};
110.平衡二叉树
力扣题目链接(opens new window)
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]

返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]

返回 false 。
题外话
咋眼一看这道题目和104.二叉树的最大深度 (opens new window)很像,其实有很大区别。
这里强调一波概念:
二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。
但leetcode中强调的深度和高度很明显是按照节点来计算的,如图
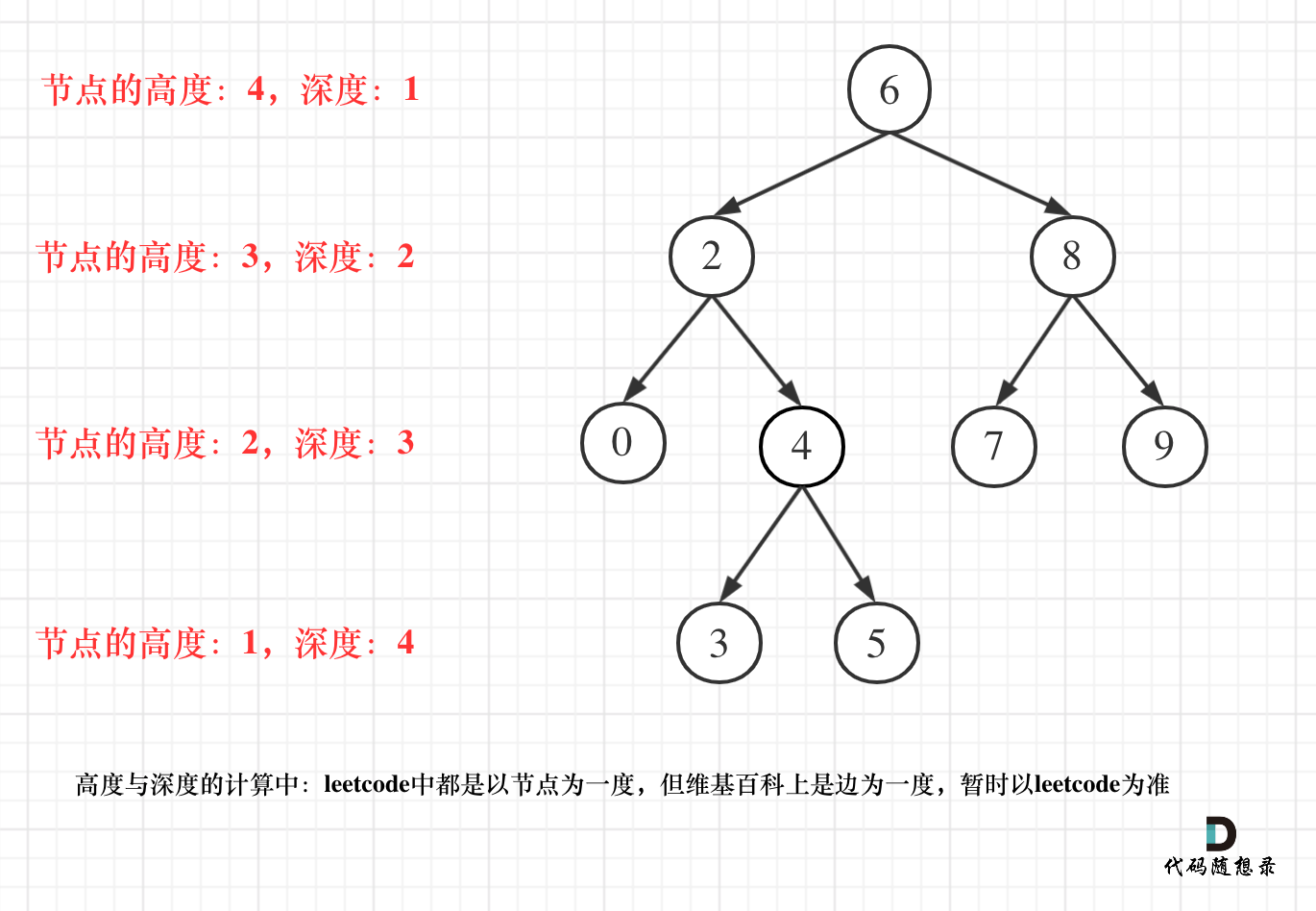
关于根节点的深度究竟是1 还是 0,不同的地方有不一样的标准,leetcode的题目中都是以节点为一度,即根节点深度是1。但维基百科上定义用边为一度,即根节点的深度是0,我们暂时以leetcode为准(毕竟要在这上面刷题)。
因为求深度可以从上到下去查 所以需要前序遍历(中左右),而高度只能从下到上去查,所以只能后序遍历(左右中)
有的同学一定疑惑,为什么104.二叉树的最大深度 (opens new window)中求的是二叉树的最大深度,也用的是后序遍历。
那是因为代码的逻辑其实是求的根节点的高度,而根节点的高度就是这棵树的最大深度,所以才可以使用后序遍历。
在104.二叉树的最大深度 (opens new window)中,如果真正求取二叉树的最大深度,代码应该写成如下:(前序遍历)
int result;
void getDepth(TreeNode* node, int depth) {
result = depth > result ? depth : result; // 中
if (node->left == NULL && node->right == NULL) return ;
if (node->left) { // 左
depth++;// 深度+1
getDepth(node->left, depth);
depth--;// 回溯,深度-1
}
if (node->right) { // 右
depth++;// 深度+1
getDepth(node->right, depth);
depth--;// 回溯,深度-1
}
return ;
}
int maxDepth(TreeNode* root) {
result = 0;
if (root == NULL) return result;
getDepth(root, 1);
return result;
}
可以看出使用了前序(中左右)的遍历顺序,这才是真正求深度的逻辑!
注意以上代码是为了把细节体现出来,简化一下代码如下:
int result;
void getDepth(TreeNode* node, int depth) {
result = depth > result ? depth : result; // 中
if (node->left == NULL && node->right == NULL) return ;
if (node->left) { // 左
getDepth(node->left, depth + 1);
}
if (node->right) { // 右
getDepth(node->right, depth + 1);
}
return ;
}
int maxDepth(TreeNode* root) {
result = 0;
if (root == 0) return result;
getDepth(root, 1);
return result;
}
本题思路
递归
此时大家应该明白了既然要求比较高度,必然是要后序遍历。
递归三步曲分析:
明确递归函数的参数和返回值
参数:当前传入节点。 返回值:以当前传入节点为根节点的树的高度。
那么如何标记左右子树是否差值大于1呢?
如果当前传入节点为根节点的二叉树已经不是二叉平衡树了,还返回高度的话就没有意义了。
所以如果已经不是二叉平衡树了,可以返回-1 来标记已经不符合平衡树的规则了。
代码如下:
// -1 表示已经不是平衡二叉树了,否则返回值是以该节点为根节点树的高度
int getHeight(TreeNode* node)
明确终止条件
递归的过程中依然是遇到空节点了为终止,返回0,表示当前节点为根节点的树高度为0
代码如下:
if (node == NULL) {
return 0;
}
明确单层递归的逻辑
如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢?当然是其左子树高度和其右子树高度的差值。
分别求出其左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则返回-1,表示已经不是二叉平衡树了。
代码如下:
int leftHeight = getHeight(node->left); // 左
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right); // 右
if (rightHeight == -1) return -1;
int result;
if (abs(leftHeight - rightHeight) > 1) { // 中
result = -1;
} else {
result = 1 + max(leftHeight, rightHeight); // 以当前节点为根节点的树的最大高度
}
return result;
代码精简之后如下:
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
此时递归的函数就已经写出来了,这个递归的函数传入节点指针,返回以该节点为根节点的二叉树的高度,如果不是二叉平衡树,则返回-1。
getHeight整体代码如下:
int getHeight(TreeNode* node) {
if (node == NULL) {
return 0;
}
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
}
最后本题整体递归代码如下:
class Solution {
public:
// 返回以该节点为根节点的二叉树的高度,如果不是平衡二叉树了则返回-1
int getHeight(TreeNode* node) {
if (node == NULL) {
return 0;
}
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
}
bool isBalanced(TreeNode* root) {
return getHeight(root) == -1 ? false : true;
}
};
迭代
在104.二叉树的最大深度 (opens new window)中我们可以使用层序遍历来求深度,但是就不能直接用层序遍历来求高度了,这就体现出求高度和求深度的不同。
本题的迭代方式可以先定义一个函数,专门用来求高度。
这个函数通过栈模拟的后序遍历找每一个节点的高度(其实是通过求传入节点为根节点的最大深度来求的高度)
代码如下:
// cur节点的最大深度,就是cur的高度
int getDepth(TreeNode* cur) {
stack<TreeNode*> st;
if (cur != NULL) st.push(cur);
int depth = 0; // 记录深度
int result = 0;
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
st.push(node); // 中
st.push(NULL);
depth++;
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left);// 左
} else {
st.pop();
node = st.top();
st.pop();
depth--;
}
result = result > depth ? result : depth;
}
return result;
}
然后再用栈来模拟后序遍历,遍历每一个节点的时候,再去判断左右孩子的高度是否符合,代码如下:
bool isBalanced(TreeNode* root) {
stack<TreeNode*> st;
if (root == NULL) return true;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top(); // 中
st.pop();
if (abs(getDepth(node->left) - getDepth(node->right)) > 1) { // 判断左右孩子高度是否符合
return false;
}
if (node->right) st.push(node->right); // 右(空节点不入栈)
if (node->left) st.push(node->left); // 左(空节点不入栈)
}
return true;
}
整体代码如下:
class Solution {
private:
int getDepth(TreeNode* cur) {
stack<TreeNode*> st;
if (cur != NULL) st.push(cur);
int depth = 0; // 记录深度
int result = 0;
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
st.push(node); // 中
st.push(NULL);
depth++;
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left);// 左
} else {
st.pop();
node = st.top();
st.pop();
depth--;
}
result = result > depth ? result : depth;
}
return result;
}
public:
bool isBalanced(TreeNode* root) {
stack<TreeNode*> st;
if (root == NULL) return true;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top(); // 中
st.pop();
if (abs(getDepth(node->left) - getDepth(node->right)) > 1) {
return false;
}
if (node->right) st.push(node->right); // 右(空节点不入栈)
if (node->left) st.push(node->left); // 左(空节点不入栈)
}
return true;
}
};
当然此题用迭代法,其实效率很低,因为没有很好的模拟回溯的过程,所以迭代法有很多重复的计算。
虽然理论上所有的递归都可以用迭代来实现,但是有的场景难度可能比较大。
例如:都知道回溯法其实就是递归,但是很少人用迭代的方式去实现回溯算法!
因为对于回溯算法已经是非常复杂的递归了,如果再用迭代的话,就是自己给自己找麻烦,效率也并不一定高。
总结
通过本题可以了解求二叉树深度 和 二叉树高度的差异,求深度适合用前序遍历,而求高度适合用后序遍历。
本题迭代法其实有点复杂,大家可以有一个思路,也不一定说非要写出来。
但是递归方式是一定要掌握的!
以为只用了递归,其实还用了回溯
257. 二叉树的所有路径
力扣题目链接(opens new window)
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
示例:

思路
这道题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径。
在这道题目中将第一次涉及到回溯,因为我们要把路径记录下来,需要回溯来回退一个路径再进入另一个路径。
前序遍历以及回溯的过程如图:
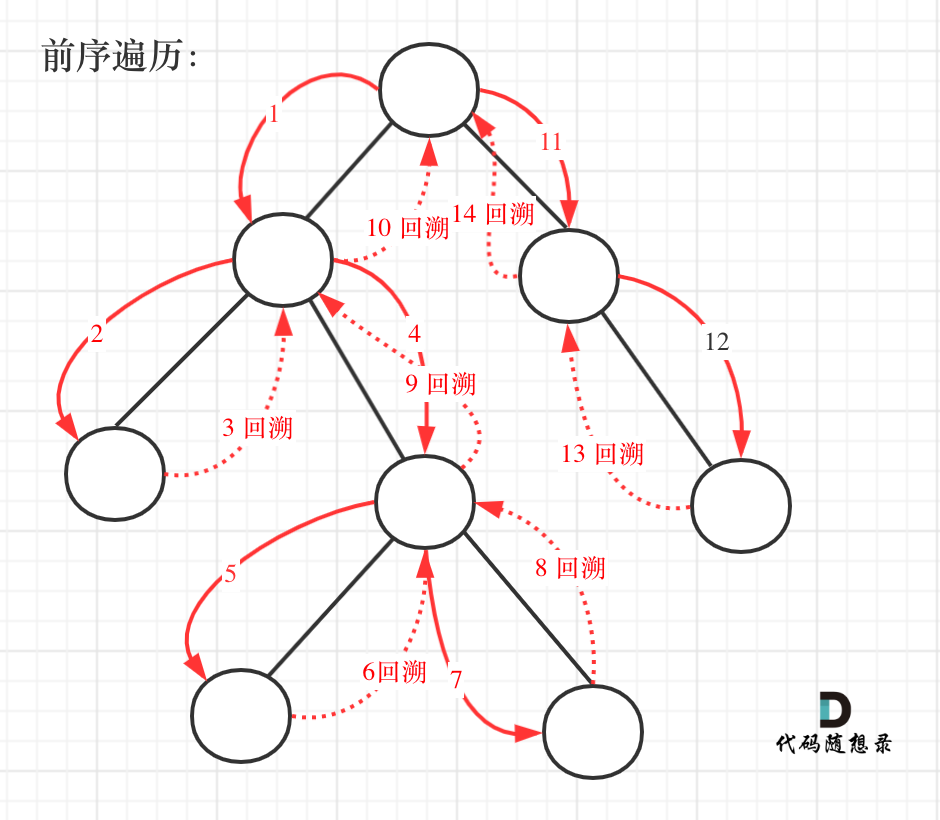
我们先使用递归的方式,来做前序遍历。要知道递归和回溯就是一家的,本题也需要回溯。
递归
递归函数参数以及返回值
要传入根节点,记录每一条路径的path,和存放结果集的result,这里递归不需要返回值,代码如下:
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result)
确定递归终止条件
在写递归的时候都习惯了这么写:
if (cur == NULL) {
终止处理逻辑
}
但是本题的终止条件这样写会很麻烦,因为本题要找到叶子节点,就开始结束的处理逻辑了(把路径放进result里)。
那么什么时候算是找到了叶子节点? 是当 cur不为空,其左右孩子都为空的时候,就找到叶子节点。
所以本题的终止条件是:
if (cur->left == NULL && cur->right == NULL) {
终止处理逻辑
}
为什么没有判断cur是否为空呢,因为下面的逻辑可以控制空节点不入循环。
再来看一下终止处理的逻辑。
这里使用vector 结构path来记录路径,所以要把vector 结构的path转为string格式,再把这个string 放进 result里。
那么为什么使用了vector 结构来记录路径呢? 因为在下面处理单层递归逻辑的时候,要做回溯,使用vector方便来做回溯。
可能有的同学问了,我看有些人的代码也没有回溯啊。
其实是有回溯的,只不过隐藏在函数调用时的参数赋值里,下文我还会提到。
这里我们先使用vector结构的path容器来记录路径,那么终止处理逻辑如下:
if (cur->left == NULL && cur->right == NULL) { // 遇到叶子节点
string sPath;
for (int i = 0; i < path.size() - 1; i++) { // 将path里记录的路径转为string格式
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]); // 记录最后一个节点(叶子节点)
result.push_back(sPath); // 收集一个路径
return;
}
确定单层递归逻辑
因为是前序遍历,需要先处理中间节点,中间节点就是我们要记录路径上的节点,先放进path中。
path.push_back(cur->val);
然后是递归和回溯的过程,上面说过没有判断cur是否为空,那么在这里递归的时候,如果为空就不进行下一层递归了。
所以递归前要加上判断语句,下面要递归的节点是否为空,如下
if (cur->left) {
traversal(cur->left, path, result);
}
if (cur->right) {
traversal(cur->right, path, result);
}
此时还没完,递归完,要做回溯啊,因为path 不能一直加入节点,它还要删节点,然后才能加入新的节点。
那么回溯要怎么回溯呢,一些同学会这么写,如下:
if (cur->left) {
traversal(cur->left, path, result);
}
if (cur->right) {
traversal(cur->right, path, result);
}
path.pop_back();
这个回溯就有很大的问题,我们知道,回溯和递归是一一对应的,有一个递归,就要有一个回溯,这么写的话相当于把递归和回溯拆开了, 一个在花括号里,一个在花括号外。
所以回溯要和递归永远在一起,世界上最遥远的距离是你在花括号里,而我在花括号外!
那么代码应该这么写:
if (cur->left) {
traversal(cur->left, path, result);
path.pop_back(); // 回溯
}
if (cur->right) {
traversal(cur->right, path, result);
path.pop_back(); // 回溯
}
那么本题整体代码如下:
// 版本一
class Solution {
private:
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
path.push_back(cur->val); // 中,中为什么写在这里,因为最后一个节点也要加入到path中
// 这才到了叶子节点
if (cur->left == NULL && cur->right == NULL) {
string sPath;
for (int i = 0; i < path.size() - 1; i++) {
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]);
result.push_back(sPath);
return;
}
if (cur->left) { // 左
traversal(cur->left, path, result);
path.pop_back(); // 回溯
}
if (cur->right) { // 右
traversal(cur->right, path, result);
path.pop_back(); // 回溯
}
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
vector<int> path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
如上的C++代码充分体现了回溯。
那么如上代码可以精简成如下代码:
class Solution {
private:
void traversal(TreeNode* cur, string path, vector<string>& result) {
path += to_string(cur->val); // 中
if (cur->left == NULL && cur->right == NULL) {
result.push_back(path);
return;
}
if (cur->left) traversal(cur->left, path + "->", result); // 左
if (cur->right) traversal(cur->right, path + "->", result); // 右
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
string path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
如上代码精简了不少,也隐藏了不少东西。
注意在函数定义的时候void traversal(TreeNode* cur, string path, vector
那么在如上代码中,貌似没有看到回溯的逻辑,其实不然,回溯就隐藏在traversal(cur->left, path + "->", result);中的 path + "->"。 每次函数调用完,path依然是没有加上"->" 的,这就是回溯了。
为了把这份精简代码的回溯过程展现出来,大家可以试一试把:
if (cur->left) traversal(cur->left, path + "->", result); // 左 回溯就隐藏在这里
改成如下代码:
path += "->";
traversal(cur->left, path, result); // 左
即:
if (cur->left) {
path += "->";
traversal(cur->left, path, result); // 左
}
if (cur->right) {
path += "->";
traversal(cur->right, path, result); // 右
}
此时就没有回溯了,这个代码就是通过不了的了。
如果想把回溯加上,就要 在上面代码的基础上,加上回溯,就可以AC了。
if (cur->left) {
path += "->";
traversal(cur->left, path, result); // 左
path.pop_back(); // 回溯 '>'
path.pop_back(); // 回溯 '-'
}
if (cur->right) {
path += "->";
traversal(cur->right, path, result); // 右
path.pop_back(); // 回溯 '>'
path.pop_back(); // 回溯 '-'
}
整体代码如下:
//版本二
class Solution {
private:
void traversal(TreeNode* cur, string path, vector<string>& result) {
path += to_string(cur->val); // 中,中为什么写在这里,因为最后一个节点也要加入到path中
if (cur->left == NULL && cur->right == NULL) {
result.push_back(path);
return;
}
if (cur->left) {
path += "->";
traversal(cur->left, path, result); // 左
path.pop_back(); // 回溯 '>'
path.pop_back(); // 回溯 '-'
}
if (cur->right) {
path += "->";
traversal(cur->right, path, result); // 右
path.pop_back(); // 回溯'>'
path.pop_back(); // 回溯 '-'
}
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
string path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
大家应该可以感受出来,如果把 path + "->"作为函数参数就是可以的,因为并没有改变path的数值,执行完递归函数之后,path依然是之前的数值(相当于回溯了)
综合以上,第二种递归的代码虽然精简但把很多重要的点隐藏在了代码细节里,第一种递归写法虽然代码多一些,但是把每一个逻辑处理都完整的展现出来了。
拓展
这里讲解本题解的写法逻辑以及一些更具体的细节,下面的讲解中,涉及到C++语法特性,如果不是C++的录友,就可以不看了,避免越看越晕。
如果是C++的录友,建议本题独立刷过两遍,再看下面的讲解,同样避免越看越晕,造成不必要的负担。
在第二版本的代码中,其实仅仅是回溯了 -> 部分(调用两次pop_back,一个pop> 一次pop-),大家应该疑惑那么 path += to_string(cur->val); 这一步为什么没有回溯呢? 一条路径能持续加节点 不做回溯吗?
其实关键还在于 参数,使用的是 string path,这里并没有加上引用& ,即本层递归中,path + 该节点数值,但该层递归结束,上一层path的数值并不会受到任何影响。 如图所示:
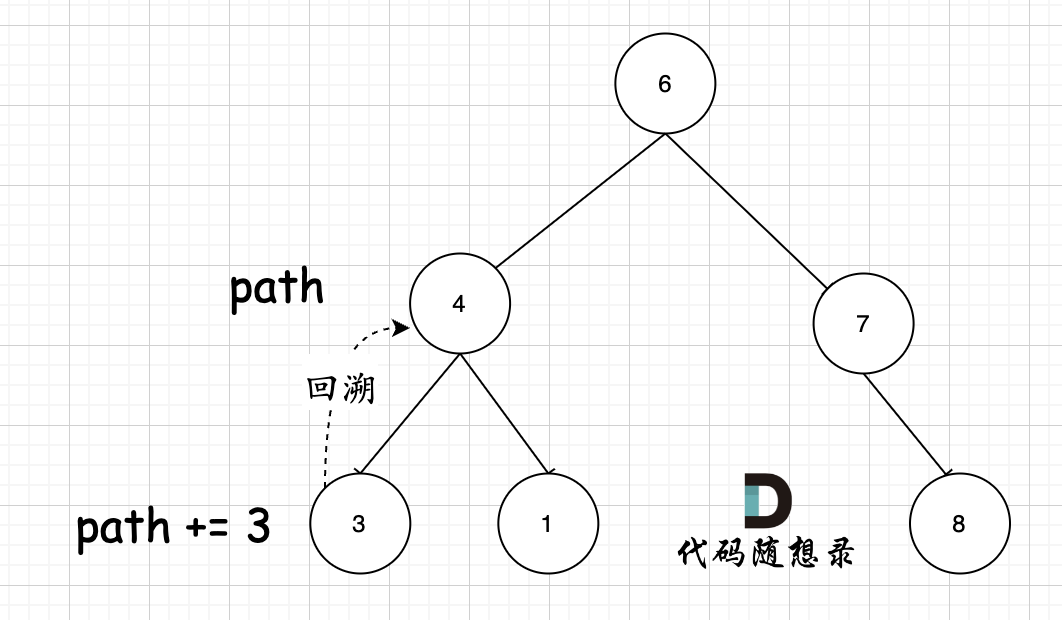
节点4 的path,在遍历到节点3,path+3,遍历节点3的递归结束之后,返回节点4(回溯的过程),path并不会把3加上。
所以这是参数中,不带引用,不做地址拷贝,只做内容拷贝的效果。(这里涉及到C++引用方面的知识)
在第一个版本中,函数参数我就使用了引用,即 vector
那有同学可能想,为什么不去定义一个 string& path 这样的函数参数呢,然后也可能在递归函数中展现回溯的过程,但关键在于,path += to_string(cur->val); 每次是加上一个数字,这个数字如果是个位数,那好说,就调用一次path.pop_back(),但如果是 十位数,百位数,千位数呢? 百位数就要调用三次path.pop_back(),才能实现对应的回溯操作,这样代码实现就太冗余了。
所以,第一个代码版本中,我才使用 vector 类型的path,这样方便给大家演示代码中回溯的操作。 vector类型的path,不管 每次 路径收集的数字是几位数,总之一定是int,所以就一次 pop_back就可以。
迭代法
至于非递归的方式,我们可以依然可以使用前序遍历的迭代方式来模拟遍历路径的过程,对该迭代方式不了解的同学,可以看文章二叉树:听说递归能做的,栈也能做! (opens new window)和二叉树:前中后序迭代方式统一写法 (opens new window)。
这里除了模拟递归需要一个栈,同时还需要一个栈来存放对应的遍历路径。
C++代码如下:
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
stack<TreeNode*> treeSt;// 保存树的遍历节点
stack<string> pathSt; // 保存遍历路径的节点
vector<string> result; // 保存最终路径集合
if (root == NULL) return result;
treeSt.push(root);
pathSt.push(to_string(root->val));
while (!treeSt.empty()) {
TreeNode* node = treeSt.top(); treeSt.pop(); // 取出节点 中
string path = pathSt.top();pathSt.pop();// 取出该节点对应的路径
if (node->left == NULL && node->right == NULL) { // 遇到叶子节点
result.push_back(path);
}
if (node->right) { // 右
treeSt.push(node->right);
pathSt.push(path + "->" + to_string(node->right->val));
}
if (node->left) { // 左
treeSt.push(node->left);
pathSt.push(path + "->" + to_string(node->left->val));
}
}
return result;
}
};
当然,使用java的同学,可以直接定义一个成员变量为object的栈Stack
标签:遍历,TreeNode,struct,int,queue,二叉树,节点 From: https://www.cnblogs.com/lulixiu1999/p/18030761