零、基本概念
直接走 OIwiki 或者看蓝书吧。
一、Ford-Fulkerson 增广
“该方法运用贪心的思想,通过寻找增广路来更新并求解最大流。”
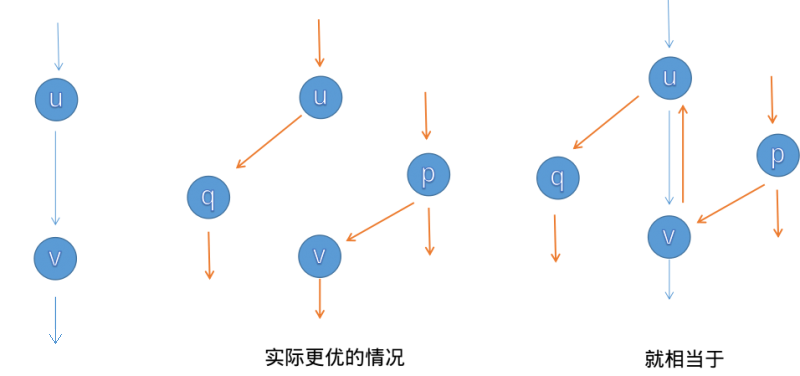
主要流程就是每次选一些增广路,以来更新最大流。但这个贪心思路不一定能保证正确性。Ford-Fulkerson 增广的核心技术是通过设置 反向边 来实现反悔贪心。
反向边的特性:流量与正向边互为相反数,且始终不大于零。
以下的 Edmonds-Karp、Dinic 和 ISAP 都是基于 Ford-Fulkerson 增广的算法。
二、Edmonds-Karp
基本流程:每次用 Bfs 选择边数最少的一条增广路,如此反复,直到没有增广路。
可以证明,增广总轮数的上界为 \(O(nm)\),单次 Bfs 的时间复杂度为 \(O(m)\),因此总复杂度为 \(O(nm^2)\)。
点击查看代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 205, MAXM = 5005;
int n, m, s, t, head[MAXN], pre[MAXN];
ll f[MAXN], maxflow;
bool vst[MAXN];
struct node{
int to, nxt;
ll wi;
} edge[MAXM*2];
inline void Add_edge(int i, int from, int to, int wi){
edge[i].to = to;
edge[i].wi = wi;
edge[i].nxt = head[from];
head[from] = i;
return;
}
inline bool Bfs(){
memset(vst, false, sizeof(vst));
memset(f, 0x3f3f, sizeof(f));//f:到当前节点为止,增广路上的最小边
queue<int> que; que.push(s); vst[s] = true;
while(!que.empty()){
int cur = que.front(); que.pop();
for(int i = head[cur]; i; i = edge[i].nxt){
if(!edge[i].wi) continue;
int to = edge[i].to;
if(vst[to]) continue;
f[to] = min(f[cur], edge[i].wi);
pre[to] = i;
vst[to] = true;
que.push(to);
if(to == t) return true;
}
}
return false;
}
inline void Update(){
for(int x = pre[t]; x; x = pre[edge[x^1].to])
edge[x].wi -= f[t], edge[x^1].wi += f[t];
maxflow += f[t];
return;
}
int main(){
scanf("%d%d%d%d", &n, &m, &s, &t);
for(int i = 1; i <= m; i++){
int ui, vi, wi; scanf("%d%d%d", &ui, &vi, &wi);
Add_edge(i*2, ui, vi, wi); Add_edge(i*2+1, vi, ui, 0);
}
while(Bfs()) Update();
cout<<maxflow;
return 0;
}