题意简述
给定 \(n\) 个点,要求构造出一棵树,同时有 \(m\) 个事件,第 \(i\) 个事件要求 \(u_i\) 和 \(v_i\) 用两条树边连接,即当中相隔一个点。若存在构造方案,输出 Yes 并输出其中一种方案,否则输出 No。
思维路径
首先简化问题,假如我们想让一堆点互相相隔一个点,我们的做法。考虑菊花图(如下图),所有绿色的点都恰好相隔一个点(中间的黑点),可以满足条件。
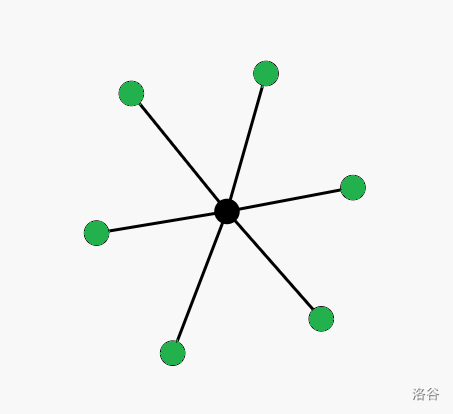
接下去考虑继续扩展,假如有很多像绿点这样的集团,都有求互相相隔一个点,我们可以对于每个集团选择一个首领,把首领串成一条链,剩下的集团连相邻的首领上。如图所示,同一种颜色位同一个集团。
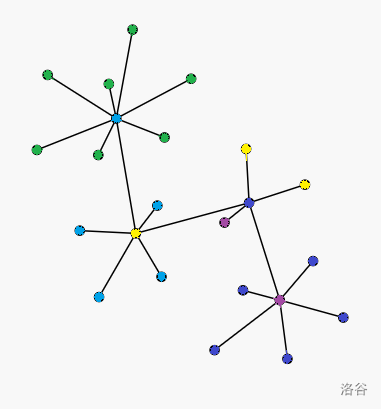
请注意,对于上面这种情况我的构造方案是将集团 \(i\) 的点连在 \(i+1\) 上,对于最后一个集团连在它的前一个上。
但是这与题目并非完全一致。我们将集团的定义改为对于任意集团内的点 \(u\),必定存在集团内另一个点 \(v\) 要求与 \(u\) 相隔为 1 个点。
此时就需要证明,之前的构造对于这个定义能够得到正确答案。
- 假设当前点 \(v\) 是首领,那么点 \(u\) 连在旁边的首领上,可以满足条件。
- 假设当前点 \(v\) 不是首领,已经连在了旁边的首领上,那么点 \(u\) 也连在旁边的首领上,可以满足条件。
综上所述之前的构造方案是可以在这个定义的前提下得到正确答案的。
实现细节
寻找集团的方式可以用并查集,首领就自动为并查集最终找到的祖先即可。
假若最终只剩下一个集团就无解。
具体实现可以参考 AC 代码。
AC 代码
#include<bits/stdc++.h>
using namespace std;
const int N=300009;
int T;
int n,m,nC;
int fa[N],cn[N],t[N];
void init(){
cin>>T;
}
void input(){
cin>>n>>m;
}
int findfa(int u){
if(fa[u]==u) return u;
else return fa[u]=findfa(fa[u]);
}
void add(int u,int v){
int fu=findfa(u);
int fv=findfa(v);
if(fu==fv) return;
fa[fu]=fv;
}
void solve(){
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
add(u,v);
}
nC=0;
for(int i=1;i<=n;i++){
if(fa[i]==i){
cn[++nC]=i;
t[cn[nC-1]]=i;//记录相邻的下一个点
}
}
if(nC==1){
cout<<"No\n";
return;
}
cout<<"Yes\n";
t[cn[nC]]=cn[nC-1];//最后一个点连到上一个点
for(int i=1;i<nC;i++){//连首领
cout<<cn[i]<<" "<<cn[i+1]<<"\n";
}
for(int i=1;i<=n;i++){//连其他点
if(fa[i]==i) continue;
cout<<i<<" "<<t[findfa(i)]<<"\n";
}
}
int main(){
init();
while(T--){
input();
solve();
}
return 0;
}
后记
和出题人给出的构造好像有些许不同,但本质是一样的。
标签:洛谷,首领,int,题解,void,集团,fa,P10179,一个点 From: https://www.cnblogs.com/lemon-cyy/p/18022369