P3195

• 斜率优化

• 暴力转移：

  • \(f(i)\) 表示考虑到第 \(i\) 个玩具达成的最小费用
  • \(f(i) = min(f(j) + (i - j + \sum_{j + 1}^{i} c - L) ^ 2)\)
  • 设 \(s_i = \sum_1^i + i\)
  • \(f(i) = min(f(j) + (s_i - s_j - 1 - L) ^ 2)\)
  • 不妨设 \(L = L + 1\)
  • \(f(i) = min(f(j) + (s_i - s_j - L) ^ 2)\)​

• 消掉常数项 \(f(j) + (s_j + L) ^ 2 - 2s_is_j\)

  • 设 \(g(i) = f(i) + (s_i + L) ^ 2\)

• 设 \(j < k < i\) 且 \(f(j) \ge f(k)\)

  • 则 $g(k) -2s_is_k \le g(j) - 2s_is_j $
  • \(\frac{g(k) - g(j)}{s_k - s_j} \le -2s_i\)​

• 

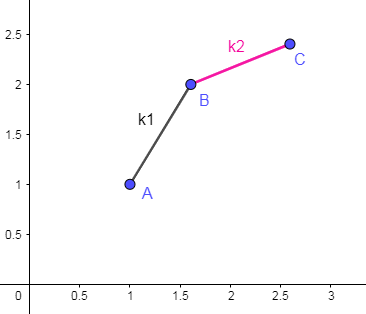
• 设点 \(A, B, C = (s_i, f(i) + (s_i + L) ^ 2)\)

  • 设 $2s_i = s_0 $ 斜率为 \(k_1, k_2\)
  • 若 \(s_0 \le k_1 \le k_2\) 则 A > B > C
  • 若 \(k_2 \le s_0 \le k_1\) 则 A, C > B
  • 若 \(k_2 \le k_1 \le s_0\)​则 C > B > A

• 跟 B 始终无关 -> A, C 连边构成下凸包

• 关于代码

  • Slope(q[l + 1], q[l]) <= 2.0 * sum[i] 说明 q[l + 1] > q[l]， 舍弃 q[l]
  • Slope(q[r], q[r - 1]) >= Slope(i, q[r]) 说明 i > q[r] > q[r - 1]，舍弃 q[r - 1]

# include <bits/stdc++.h>
# define int long long
# define double long double
using namespace std;
const int MOD = (int)1e9 + 7;
const int N = (int)1e6 + 10;

int n, ll;
int c[N], sum[N];
int q[N], l, r;
int dp[N];

int X(int x){
	return sum[x];	//
}

int Y(int x){
	return dp[x] + (sum[x] + ll) * (sum[x] + ll);
}

double Slope(int x, int y){
	return 1.0 * (Y(x) - Y(y)) / (X(x) - X(y));
}

signed main(){
//	freopen("1.in", "r", stdin);
	cin >> n >> ll;
	for(int i = 1; i <= n; i++){
		cin >> c[i];
		sum[i] = sum[i - 1] + (c[i] + 1);
	}
	ll++;	// ll 和 1 合并， 见式子 
	
	l = 1, r = 1;
	q[1] = 0;
	for(int i = 1; i <= n; i++){
		while(l < r && Slope(q[l + 1], q[l]) <= 2.0 * sum[i]){
			l++;
		}
		int j = q[l];
		dp[i] = dp[j] + (sum[i] - sum[j] - ll) * (sum[i] - sum[j] - ll);
		while(l < r && Slope(q[r], q[r - 1]) >= Slope(i, q[r])) {
			r--;
		}
		q[++r] = i;
	}
	cout << dp[n] << "\n";
}

注：a > b 表示 a 比 b 优