DFS(深度优先搜索)
顾名思义,深度优先搜索,即搜索的一种;
在搜索时,优先向下一深度搜索,可以称作回溯法。
主要实现方法是依靠递归函数;
样例
若使用DFS的搜索方法;
在下图树各点中的遍历方法为:
0 - > 1 - > 3 - > 5 - >3 - > 6 - > 3 - > 1 - > 4 - > 7 - > 9 - > 7 - > 4 - > 1 - > 0 - > 2 - > 8 - >9;
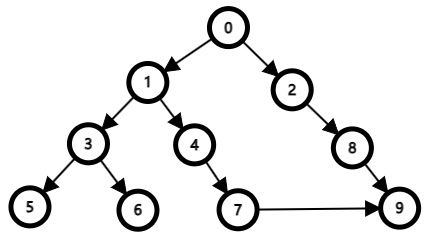
可以看到遍历方法优先增加深度(即 层数)
即能向下一层移动,就先向下一层移动,若没有,则回溯到上一层
可以说是 《长驱直入》,也可以说是一条路走到黑(再回头);
典型的递归(不是吗)
DFS模版
int dfs(int t)
{
if(满足输出条件) //即递归出口
{
输出解; //若有特殊输出格式,用自定义的 void print 函数
}
else
{
for(int i=1;i<=尝试方法数;i++)
if(满足进一步搜索条件)
{
为进一步搜索所需要的状态打上标记;
dfs(t+1);
恢复到打标记前的状态;//也就是说的{回溯一步}
}
}
}
此上为DFS的模版(一般的)可以看出主要依靠不断回溯来找到问题的解;
注意事项:
-
第一个if是符合输出解的条件,第二个
if是符合进一步搜索的条件; -
下一步搜索时,不是使用
return dfs(t+1)而是直接dfs(t+1)(可能会注意不到这个关键的地方,以至于每次写完不知道为什么只得到一个答案就返回主程序了)
-
for循环之后的if可以是多个; -
for循环边界
例题
拿P1706来说
按照字典序输出自然数 1 到 n 所有不重复的排列;
可以看出输出解的条件为当前已选的数的个数为n时,打印解(用print函数);
否则继续搜索;
代码如下:
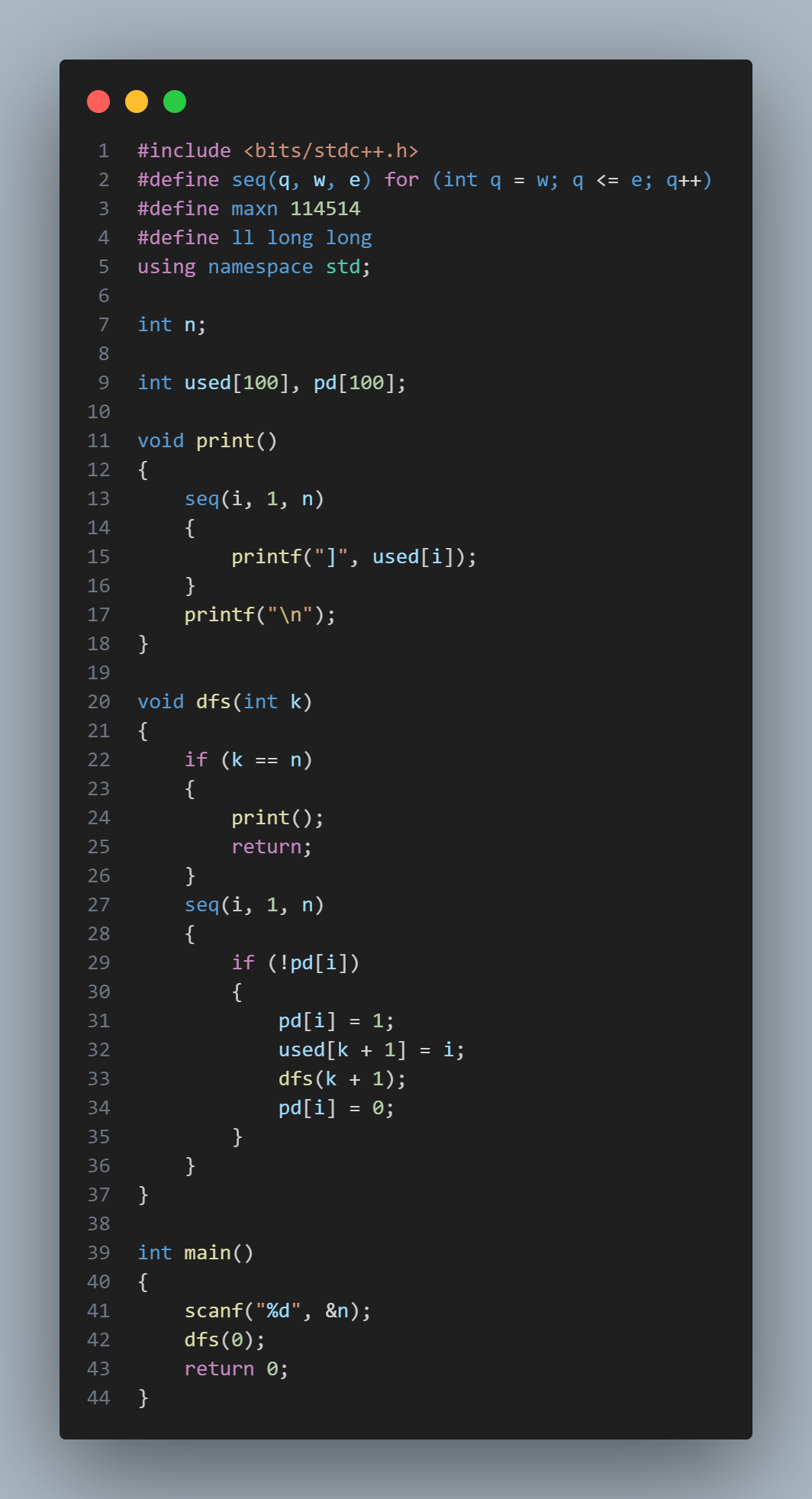
后记
不过这种方法也有不足之处

也用此图解释,若解为 $2$ 时,这时遍历左半边树是完全没有必要的;
当然我们也有解决的办法(即广度优先搜索(BFS))
这也就显现出了DFS与BFS的不同和各自的适用范围
DFS: 有多少组解的问题
BFS:最优解问题
标签:输出,优先,DFS,BFS,搜索,深度 From: https://www.cnblogs.com/adsd45666/p/18018764