首页 > 其他分享 >2024.2.16

2024.2.16

时间：2024-02-17 09:02:51浏览次数：26  
标签：std 2024.2 16 int ll now dp SIZE

寄

算是比较难的树形dp了吧。。。

我的跟题解做法不太一样，是维护2个数组 \(dp_{0/1,i}\) 和 \(f_{0/1,i}\)。不太好说，看题解做法吧QAQ。

原神 


#include <bits/stdc++.h>

typedef long long ll;

const ll SIZE = 10000 + 100;

ll N, M, a[SIZE];
ll C;

ll cnt = 1, head[SIZE], next[SIZE * 2], to[SIZE * 2];
ll value[SIZE * 2];
ll key[SIZE];

ll dp[2][SIZE];//dp[0][now] 表示now为中转站的最小花费 dp[1][now] 表示now不为中转站的最小花费

void AddEdge(ll u, ll v, ll w) {
    ++ cnt;
    next[cnt] = head[u];
    head[u] = cnt;
    to[cnt] = v;
    value[cnt] = w;
}

ll fat[SIZE];
ll f[2][SIZE];//f[0][now] 表示从儿子来的最小花费 f[1][now] 表示从父亲来的最小花费

void Dfs1(ll now, ll fa, ll dis) {
    ll sum = 0;

    f[0][now] = 0;
    for (ll i = head[now]; i; i = next[i]) {
        if (to[i] == fa)
            continue;
        Dfs1(to[i], now, dis + value[i]);
        sum += f[0][to[i]];
    }

    f[0][now] = std::min(sum + dis * key[now], std::min(dp[0][now], dp[1][now]));
}

std::pair<ll, ll> no;
ll temp[SIZE];

void Dfs3(ll now, ll fa, ll dis) {

    ll sum = 0;

    temp[now] = 0;
    for (ll i = head[now]; i; i = next[i]) {
        if (to[i] == fa || to[i] == no.first || to[i] == no.second) 
            continue;
        Dfs3(to[i], now, dis + value[i]);
        sum += temp[to[i]];
    }

    temp[now] = std::min(sum + dis * key[now], std::min(dp[0][now], dp[1][now]));
}

void Dfs2(ll now, ll fa, ll dis, ll from) {
    Dfs3(from, fat[from], dis);
    f[1][now] += temp[from];

    dp[0][from] = std::min(dp[0][from], f[1][now] + dp[1][now]);

    for (ll i = head[now]; i; i = next[i]) {
        if (to[i] == fa)
            continue;
        Dfs2(to[i], now, dis + value[i], from);
    }
    return;
}

void Dfs(ll now, ll fa) {
    ll tot = 0;

    dp[0][now] = dp[1][now] = 1e18;
    fat[now] = fa;

    for (ll i = head[now]; i; i = next[i]) {
        if (to[i] == fa)
            continue;
        tot ++;
        Dfs(to[i], now);
    }

    if (!tot) {
        dp[1][now] = C;
        return;
    }
    else {
        Dfs1(now, fa, 0);
        dp[1][now] = f[0][now] + C;
    }

    no.first = fa;

    for (ll i = head[now]; i; i = next[i]) {
        if (to[i] == fa)
            continue;
        
        no.second = to[i];
        Dfs2(to[i], now, value[i], now);
    }

}

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);

    freopen("post.in", "r", stdin);
    freopen("post.out", "w", stdout);

    std::cin >> N >> M >> C;
    
    for (ll i = 1, u, v, w; i < N; ++ i) {
        std::cin >> u >> v >> w;
        AddEdge(u, v, w);
        AddEdge(v, u, w);
    }

    for (ll i = 1; i <= M; ++ i) {
        std::cin >> a[i];
        key[a[i]] ++;
    }   

    Dfs(1, 0);

    std::cout << std::min(dp[0][1], dp[1][1]) << '\n';

    return 0;
}

摆

不会行列式和杜教筛

润

这个题好啊，我西索一下。

先知道一个性质：在分治过程中，每一层的长度只有两种可能。可以用归纳证一下。

我们先考虑单独特殊情况：选出的数是2的次幂（如：\(1000_{(2)},100_{(2)}\)）。

那么我们的分治过程如下图：

那我们这个时候如果给 \(100_{(2)}\) 加上 \(1\) 呐？

那么就成了下图：

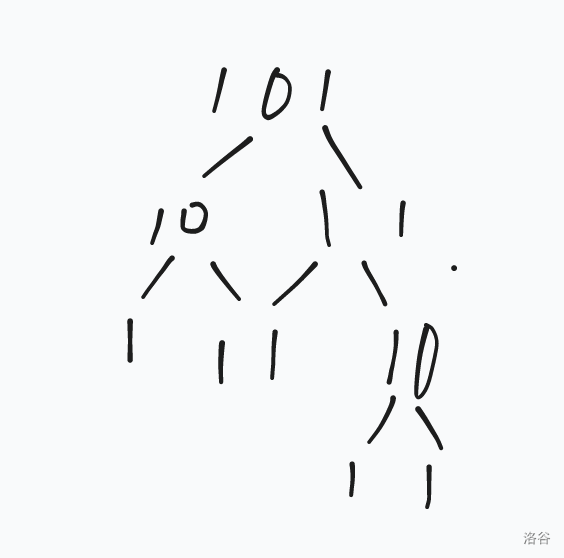
继续加一

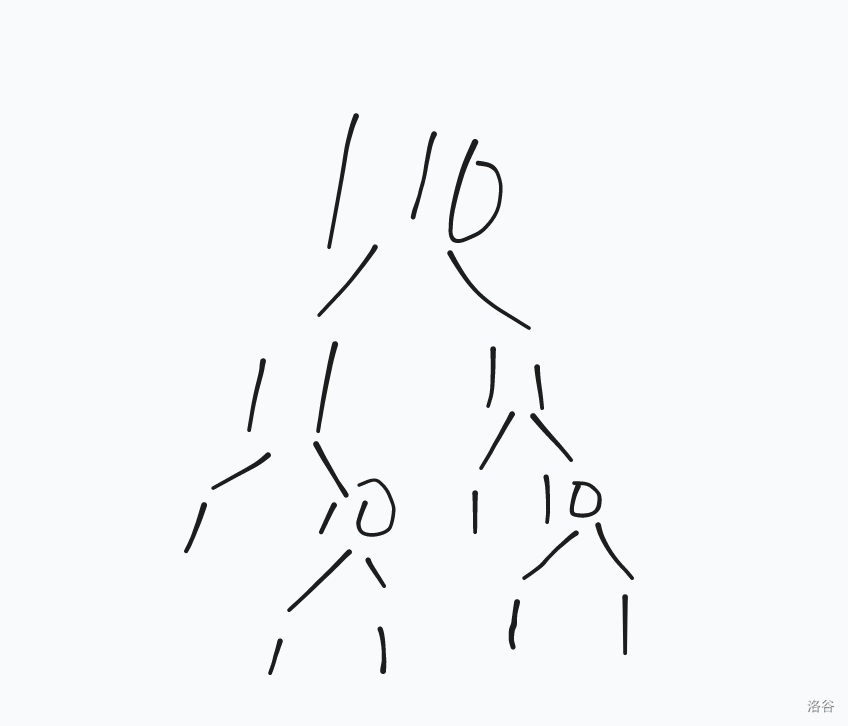
有没有发现一些规律？？？

我们先设每一层原本的二进制长度为 \(p\)。（如：\(1001_{(2)}\) 的 \(p\) 为 \(4\)）。并且设 \(x=10100_{(2)}\)

那么对于一个数 \(x\)，我们在每一位上从左往右数第 \(2\) 个 \(1\) 到最低位所表示的数（以 \(x\) 为例，是 \(100_{(2)}\)，即 \(4_{(10)}\)），是在每一层里面产生的贡献是等效于 \(2^{p}\) 的数的个数 （与每一层的节点数取min），每一层里面剩下的节点都等效于 \(2^{p-1}\)。

然后用线段树维护就行了。

崩坏：星球铁道 
#include <bits/stdc++.h>

typedef long long ll;

const int SIZE = 1e5 + 100;
const int mod = 998244353;

class Node {
public:
    int l, r;
    ll sum[2];
    int first[2];
};

int N, M;
int s[SIZE];
ll power2[SIZE];

class SegmentTree {
    #define lid (id << 1)
    #define rid (id << 1 | 1)

public:
    int tag[SIZE * 4];
    Node node[SIZE * 4];

private:
    Node pushup(Node lson, Node rson) {
        Node result;
        result.l = lson.l;
        result.r = rson.r;

        result.first[0] = std::min(lson.first[0], rson.first[0]);
        result.first[1] = std::min(lson.first[1], rson.first[1]);

        result.sum[0] = (lson.sum[0] * power2[rson.r - rson.l + 1] % mod + rson.sum[0]) % mod;
        result.sum[1] = (lson.sum[1] * power2[rson.r - rson.l + 1] % mod + rson.sum[1]) % mod;

        return result;
    }

    void Zero(Node &a) {
        a.first[0] = 1e9;
        a.sum[0] = 0;
        a.first[1] = a.l;
        a.sum[1] = (power2[a.r - a.l + 1] - 1 + mod) % mod;
    }

    void One(Node &a) {
        a.first[0] = a.l;
        a.sum[0] = (power2[a.r - a.l + 1] - 1 + mod) % mod;
        a.first[1] = 1e9;
        a.sum[1] = 0;
    }

    void Swap(Node &a) {
        std::swap(a.first[0], a.first[1]);
        std::swap(a.sum[0], a.sum[1]);
    }

    void Cover(int id, int New) {
        if (New == 1) {
            if (tag[id] == 2)
                One(node[id]), New = 3;
            else if (tag[id] == 3)
                Zero(node[id]), New = 2;
            else {
                Swap(node[id]);
                if (tag[id])
                    New = 0;
            }
        }
        else {
            if (New == 2)
                Zero(node[id]);
            else
                One(node[id]);
        }

        tag[id] = New;
    }

    void pushdown(int id) {
        if (tag[id] == 0)
            return;
        Cover(lid, tag[id]);
        Cover(rid, tag[id]);
        tag[id] = 0;
    }

public:
    void build(int id, int l, int r) {
        if (l == r) {
            if (s[l] == 1) {
                node[id].first[0] = l;
                node[id].first[1] = 1e9;
                node[id].sum[0] = 1;
                node[id].sum[1] = 0;
            }
            else {
                node[id].first[0] = 1e9;
                node[id].first[1] = l;
                node[id].sum[0] = 0;
                node[id].sum[1] = 1;
            }
            
            node[id].l = node[id].r = l;

            return;
        }

        int mid = (l + r) >> 1;

        build(lid, l, mid);
        build(rid, mid + 1, r);

        node[id] = pushup(node[lid], node[rid]);

        return;
    }

    void Update(int id, int l, int r, int askL, int askR, int flag) {
        if (askL <= l && r <= askR) {
            Cover(id, flag);
            return;
        }
        int mid = (l + r) >> 1;
        pushdown(id);
        if (askL <= mid)
            Update(lid, l, mid, askL, askR, flag);
        if (mid + 1 <= askR)
            Update(rid, mid + 1, r, askL, askR, flag);
        node[id] = pushup(node[lid], node[rid]);
    }

    Node Query(int id, int l, int r, int askL, int askR) {
        if (askL <= l && r <= askR) 
            return node[id];

        int mid = (l + r) >> 1;
        pushdown(id);

        Node result;
        result.l = result.r = result.first[0] = result.first[1] = 1e9;
        result.sum[0] = result.sum[1] = 0;

        if (askL <= mid) {
            result = Query(lid, l, mid, askL, askR);
        }
        if (mid + 1 <= askR) {
            if (result.l == 1e9)
                result = Query(rid, mid + 1, r, askL, askR);
            else
                result = pushup(result, Query(rid, mid + 1, r, askL, askR));
        }
        return result;
    }

    #undef lid
    #undef rid
}tree;

std::string str;
ll treeSum[SIZE], prefix[SIZE], powerSum[SIZE];

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    std::cout.tie(0);

    freopen("run.in", "r", stdin);
    freopen("run.out", "w", stdout);

    std::cin >> N >> M;
    power2[0] = 1;
    for (int i = 1; i <= N; ++ i) {
        power2[i] = power2[i - 1] * 2 % mod;
        treeSum[i] = (treeSum[i - 1] * 2 % mod + (1 + i - 1) * power2[i - 1] % mod) % mod;
        powerSum[i] = (powerSum[i - 1] + power2[i - 1]) % mod;
        prefix[i] = (prefix[i - 1] + power2[i - 1] * (1 + i - 1)) % mod;
    }

    std::cin >> str;
    std::reverse(str.begin(), str.end());
    for (int i = 1; i <= N; ++ i) {
        s[i] = str[i - 1] - '0';
    }
    tree.build(1, 1, N);

    for (int i = 1, opt, l, r; i <= M; ++ i) {
        std::cin >> opt >> l >> r;
        l = N - l + 1;
        r = N - r + 1;
        std::swap(l, r);

        if (opt == 4) {
            Node first = tree.Query(1, 1, N, l, r);
            if (first.first[0] == 1e9) {
                std::cout << 0 << '\n';
                continue;
            }

            ll answer = treeSum[first.r - first.first[0] + 1];
            Node second = tree.Query(1, 1, N, first.first[0] + 1, r);
            
            if (second.first[0] == 1e9) {
                std::cout << answer << '\n';
                continue;
            }

            ll val = second.sum[0];
            ll len1 = first.r - first.first[0] + 1;
            ll len2 = first.r - second.first[0] + 1;

            ll temp = power2[len1 - 1] * (len1 + len1 - len2 + 1) % mod * (len2) % mod * 499122177 % mod;
            temp = (temp + prefix[len1 - len2] * val % mod) % mod;
            answer = (answer - temp + mod) % mod;
            
            temp = (temp + power2[len1 - 1] * len2 % mod) % mod;
            temp = (temp + powerSum[len1 - len2] * val % mod) % mod * 2 % mod;
            
            answer = (answer + temp) % mod;
            answer = (answer + 2 * val) % mod;

            std::cout << answer << '\n';
        }
        else {
            tree.Update(1, 1, N, l, r, opt);
        }
    }

    return 0;
}
/*
5 1
01010
4 2 5
*/

标签：std,2024.2,16,int,ll,now,dp,SIZE
From： https://www.cnblogs.com/jueqingfeng/p/18017567

相关文章

  • 2月16日总结
    exColor作为示例，可能过于简单这里再补充一个ini解析的示例由于实在写不动用其他库解析ini了,春节都要过完了，累了，写不动了，所以随意找了一份解析ini的库，仅供参考，对比不准确，毕竟完整库包含了更多功能先看看结果BenchmarkDotNetv0.13.12,Windows11(10.0.22631.3085/23......
  • 2024-02-16-物联网C语言(数据类型与语句)
    1.第一个C语言程序#include<stdio.h>intmain(){printf("helloworld");return0;}输出结果PSD:\04_Dev\05_C\01数据类型与语句\output>&.\'01_first.exe'helloworld1.1关键字c语言已经定义好的名字，直接拿过来用即可1.1.1数据类型相关的关键字作用：用......
  • 酷睿i5-12450H+16GB内存！神舟战神Mini电脑1899元到手
    神舟战神Minii5迷你台式电脑正在参与京东年货节大促，搭载酷睿第12代i5-12450H处理器，另外还有16GBDDR4内存和512GBPCIe4.0SSD，整机到手价1899元，应该是目前为止相同配置售价最低的品牌迷你主机。酷睿第12代i5-12450H处理器其实是用于笔记本的型号，拥有超低的功耗但是性能却不低......
  • 2024/2/16学习进度笔记
    SparkStreaming支持的数据输入源很多，例如：Kafka、Flume、Twitter、ZeroMQ和简单的TCP套接字等等。数据输入后可以用Spark的高度抽象原语如：map、reduce、join、window等进行运算。而结果也能保存在很多地方，如HDFS，数据库等。另外SparkStreaming也能和MLlib（机器学习）以及G......
  • 2.16 闲话 & solution『漆黑的夜中透出了一点点微光/早就应该习惯/忽明忽暗酒阑人散』
    为啥只有我和CuFeO4【数据删除】，别人都没【数据删除】，血亏，下次绝对不【数据删除】了明天有CF，希望能打在写\(\text{NTT}\)惹，但是没有达成写4题呜呜明天有模拟赛唔，首先是朴素\(dp\)骗分，设\(dp_{i,j}\)表示已经取到了\(i\)个，其中取模后结果为\(j\)的方案数，容易有转移\[......
  • Solution Set【2024.2.16】
    A.寄（post）对于点对贡献问题考虑在最近公共祖先处计算答案，称给定的\(m\)个点为关键点，选择的\(k\)个点为选择点。既然我们已经要求了对于每一对关键点和选择点均在其最近公共祖先处计算答案，那么这也就意味着，存在某些节点，其子树中的关键点/选择点不会与其子树内的选择点/关......
  • 闲话2.16
    刚写了个唐氏鞋油，感觉自己跟唐一样......
  • 2024.2.16 そんな凡庸を探して、探している
    Namid[A]me好听呢。可惜了。今天DP专题感觉laofu选的题有点经典，导致我有一半时间在摸鱼，不过还是写了点题的。怎么西工大附中有糖醋茄子这种神秘菜啊。ICPC2020MacauBBoringProblem其实不一定懂完了，试着说一说。显然询问没什么用，问题本质是要求解一个AC自动机上游......
  • 洛谷P6169 [IOI2016] Molecules
    洛谷传送门分析结论：如果存在解，则一定有一个解使得选的数是排序后的一段前缀并上一段后缀。下文所说序列均已排序。引理：对于一个可行解选的某个数，一定可以将其换成序列中的最小数或最大数而使得换完之后还是一个可行解。证明：反证法。假设都不可换。设当前选的所有数的和为\(......
  • CF1624D【黄】-思维题
    题目：https://www.luogu.com.cn/problem/solution/CF1624D这道题很简单，但是启发我把这一类题都起名为思维题，贪心题大部分都是思维题，但还有很多不属于贪心题的思维题，总之思维题就是考察思维能力，和算法无关，通常能做出来的都能轻松做出，做不出来的想破头也想不出来，这道题属于前者。C......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99