1.BiTree层次建树实现
使用二叉树的链式存储,必须要构造一个辅助链式队列,用pcur遍历树结点,实现代码如下:
代码实现
//二叉树层次建树+画图 2024-02-12
#include <iostream>
#include <cstdio>
using namespace std;
//树结点的数据结构
typedef char ElemType;
typedef struct TNode{
ElemType c; //即data
struct TNode *lchild, *rchild; //左右孩子指针
}TNode,*Tree;
//需要一个用于辅助的链式队列
typedef struct LinkNode{
TNode * data; //用于存储树结点的地址,藏宝图
struct LinkNode *pnext;
}LinkNode;
typedef struct {
LinkNode *phead, *ptail;
}LinkQueue;
//链队列部分
//下次应该把TNode * 取个别名,这样代码更容易移植通用
bool IsEmpty(LinkQueue Q)
{
return Q.phead == NULL && Q.ptail == NULL;
}
//获取队头元素值
bool GetTop(LinkQueue Q, TNode *&x)
{
if(IsEmpty(Q))
{
return false;
}
x = Q.phead->data;
return true;
}
//入队
bool EnQueue(LinkQueue &Q, TNode *x)
{
LinkNode *pnew = (LinkNode*)calloc(1, sizeof(LinkNode));
pnew->data = x;//因为是calloc就不用pnew->pnext = NULL;
Q.ptail->pnext = pnew;
Q.ptail = pnew; //队尾指针指向新插入的最后一个结点
return true;
}
//出队,队头出队
bool DeQueue(LinkQueue &Q, TNode *&x)
{
if(IsEmpty(Q))
{
return false;
}
x = Q.phead->data;
LinkNode *q = Q.phead;
Q.phead = Q.phead->pnext;
if(Q.phead == NULL)//如果删除的是最后一个结点
{
Q.ptail = Q.phead;
}
free(q);
return true;
}
//二叉树递归遍历
//先序遍历
void preOrder(Tree T)
{
if(T != NULL)
{
printf("%c", T->c);
preOrder(T->lchild);
preOrder(T->rchild);
}
}
//abcdefghij
int main()
{
ElemType c;
Tree T = NULL;
LinkQueue Q;//定义一个用于辅助层次建树的链队列
Q.phead = Q.ptail = NULL;
LinkNode *pcur;
while(scanf("%c", &c) != EOF)
{
if(c == '\n')
break;
if(NULL == T) //如果是第一个结点,就作为根结点
{
T = (Tree)calloc(1, sizeof(TNode)); //用calloc把整个结点数据置0,即NULL
T->c = c;
LinkNode *p = (LinkNode *)calloc(1, sizeof(LinkNode));
p->data = T;
Q.phead = Q.ptail = p;
pcur = p;
continue;
}
//不是第一个输入的结点
TNode *tnew = (TNode *)calloc(1, sizeof(TNode));
tnew->c = c;
EnQueue(Q, tnew); //入队,入链队列
if(pcur->data->lchild == NULL)//建树
{
pcur->data->lchild = tnew;
}
else if(pcur->data->rchild == NULL)
{
pcur->data->rchild = tnew;
pcur = pcur->pnext;//左右孩子都满了指向链队列的下一个结点
}
}
preOrder(T);
printf("\n");
return 0;
}
画示意图如图所示:
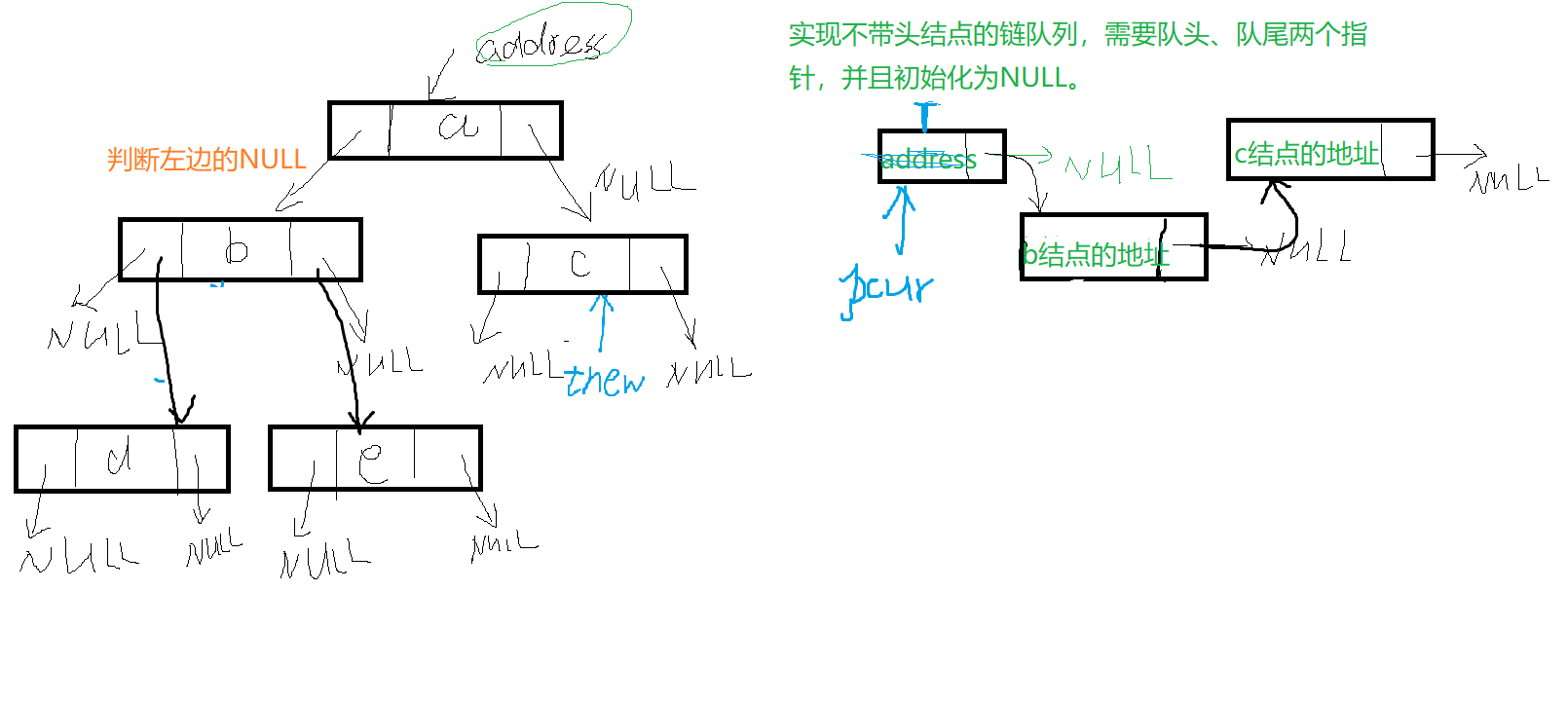
注意,calloc和malloc函数的区别,就在于calloc分配空间的同时,会把该内存空间的数据置0,方便了我们不用加一行代码使指针变量值为NULL。
2.数据结构动画网址
很好用的数据结构动画网站,不过是国外的,可能用魔法访问速度快一点。
3.前/中/后序遍历
前序遍历也叫先序遍历,如果层次遍历是广度优先遍历,那么前序遍历就是深度优先遍历。以中序遍历为例,使用递归的方法是很容易理解和实现的,并且我们手动去写出遍历的结果,也可以参照递归代码的逻辑,每次只看一小棵子树,孩子结点总是紧挨着父结点。
3.1中序遍历非递归实现
中序遍历
//中序遍历递归
void InOrder(BiTree t)
{
if (t)//要设置递归出口
{
InOrder(t->lchild);
putchar(t->c);
InOrder(t->rchild);
}
}
//中序遍历非递归,需要构思
void InOrder2(BiTree t)
{
SqStack S;
InitStack(S); BiTree p = t;
while (p || !StackEmpty(S))
{
if (p)
{//不断压栈的过程中找到最左边的左孩子
Push(S, p);
p = p->lchild;
}
else {//弹出栈中元素并打印,获取打印元素的右结点
Pop(S, p);
putchar(p->c);
p = p->rchild;
}
}
}
打印结果:
4.层次遍历(层序遍历)
看着建好的二叉树图,按逻辑写下来即可,注意和层序建树一样,需要用到一个辅助的链式队列,为了节省空间,链队列只存树结点的地址。
层序遍历
//层序遍历,需要借助一个辅助链队列,广度优先遍历
void LevelOrder(BiTree t)
{
LinkQueue Q;
InitQueue(Q);
BiTNode* p = t;
EnQueue(Q, p);//树根入队
while (!IsEmpty(Q))
{
DeQueue(Q, p);//出队当前结点并打印
putchar(p->c);
if (p->lchild)
{
EnQueue(Q, p->lchild);
}
if (p->rchild)
{
EnQueue(Q, p->rchild);
}
}
printf("\n");
}
5.中序线索二叉树
线索二叉树在实际工业中没有应用场景,不重要,它其实就是认为空着的左右孩子指针,可以利用起来,指向对应的前驱或者后继。而前驱和后继这两个概念是线性表的,所以首先要把一棵二叉树按照中序遍历,遍历成一行,然后用数组,或者辅助队列存储,再次中序遍历这棵树,在遍历途中根据我们之前保存的辅助队列中的序列,指向相应的前驱和后继,这是一个比较简单粗暴的方法。
方法二就是采用递归,以中序为例,左根右,递归左子树,访问当前结点,递归右子树,并设置当前结点指针变量p,和指向前驱结点的指针变量pre。单步调试比较复杂,涉及函数堆栈,层层进栈出栈,如果不行,就先放弃。