总体思路
本题通过每次在已知序列中加入 \(2\) 个元素的方法,可以构造出满足条件的序列 \(A\) ,这里提供一种新的构造方法。
性质
因为序列 \(A\) 中所有元素构成的可重集与序列 \(B\) 中所有元素构成的可重集完全相等,所以 \(A\) 中所有元素之和与 \(B\) 中所有元素之和相等。
\[ \sum_{i=1}^{n}B_i=\sum_{i=1}^{n}A_i \]题目中除 \(A_1\) 和 \(A_n\) 以外,所有序列 \(A\) 中的元素都对序列 \(A\) 元素的总和产生一个两份贡献。
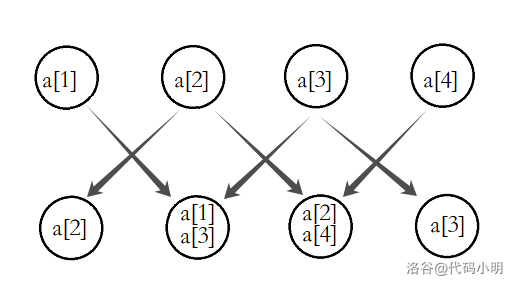
可以表示为:
\[\sum_{i=1}^{n}B_i = A_1+A_n+2 \cdot \sum_{i=2}^{n-1}A_i \]经过等量代换,我们发现序列 \(A\) 具有这样一个性质
\[\sum_{i=1}^{n}A_i = A_1+A_n+2 \cdot \sum_{i=2}^{n-1}A_i \]\[\sum_{i=2}^{n-1}A_i=0 \]构造
我们可以由此从已知序列,推出长度比此序列多 \(2\) 的新序列,具体方法如下:
我们记已知序列 \(A\) 的长度为 \(len\)。
当我们在一个已知序列 \(A\) 加入两个新元素时,假设构造出的新序列 \(A'\) 仍然满足条件。
那么根据先前推导的性质,我们可以求出新加入的第一个数:
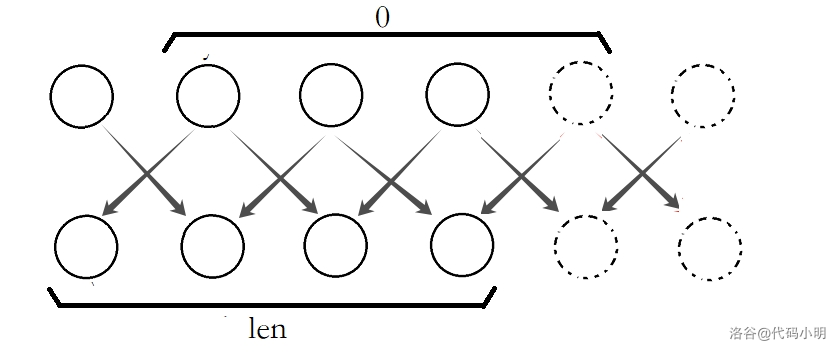
假设已知序列 \(B\) 中最后一个元素为 \(x\) ,不妨设与它相对应的元素为 \(y\)。
当我们加入新元素时,会产生新的贡献关系,从而破坏元素 \(x\) 和 \(y\) 的对应关系。
此时没有元素与 \(x\) 对应,又因为元素 \(A'_{len+1}\) 已经与 \(B'_{len+2}\) 对应,所以只能让元素 \(A'_{len+2}\) 与 \(x\) 对应:
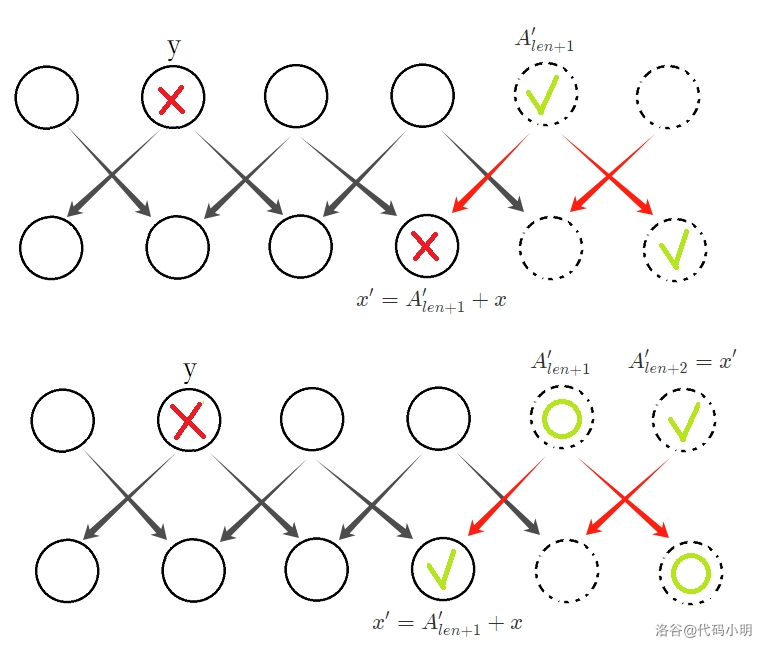
此时,我们发现除了 \(y\) 以外的元素都一一对应,那么 \(B'_{len+1}\) 自然就可以与 \(y\) 对应了。
至此,所有元素均完成配对,成功由已知序列 \(A\) 构造出比此序列多 \(2\) 的新序列 \(A'\) ,且 \(A'\) 满足题意。
实现
我们发现,在 \(n<7\) 内不能构造出一组 \(n\) 为奇数的序列 \(A\) ,此时无解。
所以我们通过构造出两组最短序列 \(A\) ,一组 \(n\) 为奇数,一组 \(n\) 为偶数,按照上文提到的方式构造即可。
\(n\) 为偶数:
2
-1 1
\(n\) 为偶数:
7
-5 8 1 -3 -4 -2 5
代码实现:
#include<bits/stdc++.h>
using namespace std;
int n;
int a[1000010];
int b[1000010];
int sum[1000010];
void init(){
if(n%2==0) a[1]=-1,a[2]=1;
else a[1]=-5,a[2]=8,a[3]=1,a[4]=-3,a[5]=-4,a[6]=-2,a[7]=5;
for(int i=1;i<=(n%2?7:2);i++){
if(i!=1) b[i-1]+=a[i];
b[i+1]+=a[i];
sum[i]=sum[i-1]+a[i];
}
}
int main(){
cin>>n;
if(n%2&&n<7){
cout<<"NO"<<endl;
return 0;
}
init();
cout<<"YES"<<endl;
for(int k=(n%2?8:3);k<=n;k+=2){
int s=sum[k-1]-sum[1];//cout<<s<<endl;
a[k]=-s;
b[k-1]+=a[k];
b[k+1]+=a[k];
a[k+1]=b[k-1];
b[k]+=a[k+1];
b[k+2]+=a[k+1];
sum[k]=sum[k-1]+a[k];
sum[k+1]=sum[k]+a[k+1];
}
for(int i=1;i<=n;i++)
cout<<a[i]<<" ";
return 0;
}