椭圆的定义

椭圆的定义

先给出椭圆第一定义：椭圆上的点到两个定点 \(F_1,F_2\) 的距离之和为定值 \(2a\)。

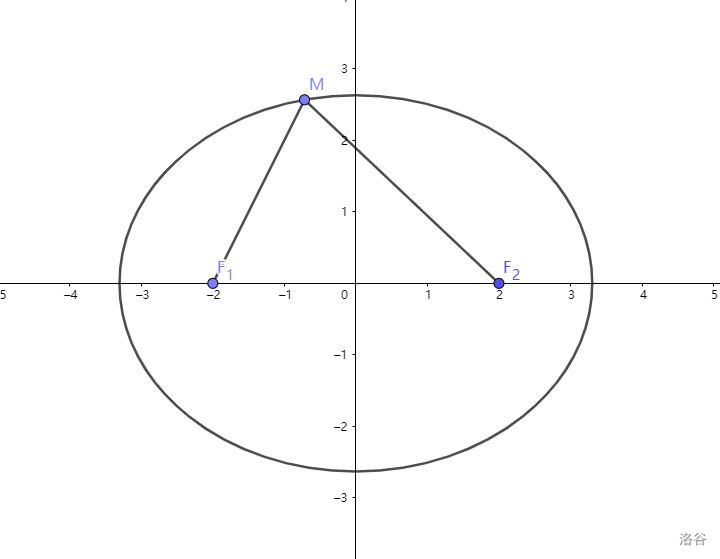
用式子表示就是：\(|MF_1|+|MF_2|=2a\)。

其中 \(F_1,F_2\) 为椭圆的焦点，有点类似于圆的圆心。

建系：以 \(F_1,F_2\) 两点形成的直线作为 \(x\) 轴，以这两点的中垂线作为 \(y\) 轴。

下面开始推导椭圆的方程：

设 \(M(x,y),F_1(-c,0),F_2(c,0)\)。\((a>0,c\not =0)\)

\(|MF_1|+|MF_2|=2a\);

\(\sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2}=2a\);

\(\sqrt{(x+c)^2+y^2}=2a-\sqrt{(x-c)^2+y^2}\);----------移项

\((x+c)^2+y^2=(2a-\sqrt{(x-c)^2+y^2})^2\);----------两边同时乘方

\(x^2+c^2+2cx+y^2=4a^2+x^2+c^2-2cx+y^2-4a\sqrt{(x-c)^2+y^2}\);----------暴拆

\(2cx=4a^2-2cx-4a\sqrt{(x-c)^2+y^2}\);----------消项

\(a\sqrt{(x-c)^2+y^2}=a^2-cx\);----------移项化简

\(a^2(x^2+c^2-2cx+y^2)=a^4+c^2x^2-2a^2cx\);----------乘方

\(a^2x^2+a^2c^2+a^2y^2=a^4+c^2x^2\);----------化简

\(a^2x^2-c^2x^2+a^2y^2=a^4-a^2c^2\);----------移项

\((a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2)\);----------提

\(\cfrac{x^2}{a^2}+\cfrac{y^2}{a^2-c^2}=1\);----------右边化为 \(1\)

令 \(b^2=a^2-c^2\);

得到 \(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\)。

注意：\(a>b>0\)

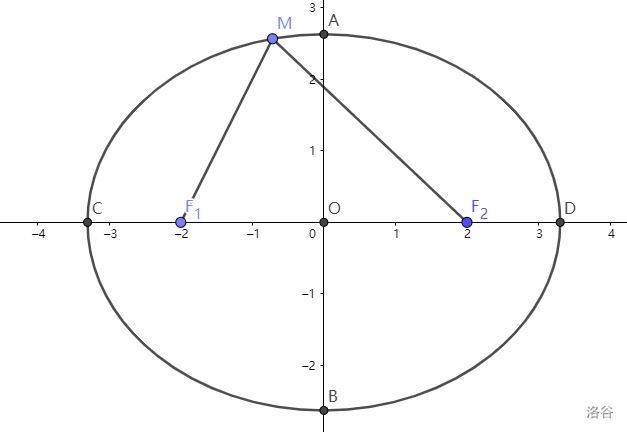
\(O\) 点是这个椭圆的对称中心，也是其中心。

\(A,B,C,D\) 是这个椭圆的四个顶点。

接下来求这四个顶点的坐标：

因为 \(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\)

令 \(x=0\);

有\(\cfrac{y^2}{b^2}=1\);

\(y_1=b,y_2=-b\)，即 \(A(b,0),B(b,0)\)。

令 \(y=0\);

有\(\cfrac{x^2}{a^2}=1\);

\(x_1=-a,x_2=a\)，即 \(C(-a,0),D(a,0)\)。

会发现 \(CD\) 的长度等于 \(2a\)，与前面 \(|MF_1|+|MF_2|=2a\) 这条式子有些联系。\(AB\) 的长度等于 \(2b\)。我们规定，长度等于 \(2a\) 的这条线段为椭圆的长轴，等于 \(2b\) 的即为短轴。长轴的长度叫作长轴长，短轴的长度叫作短轴长。所以说 椭圆上的 任意一个点 到两焦点的距离之和 是等于 长轴长的。

再给出一些定义，长轴的一半叫作长半轴，其长度叫作长半轴长，也就是 \(a\)；短轴的一半叫作短半轴，其长度叫做短半轴长，也就是 \(b\)。

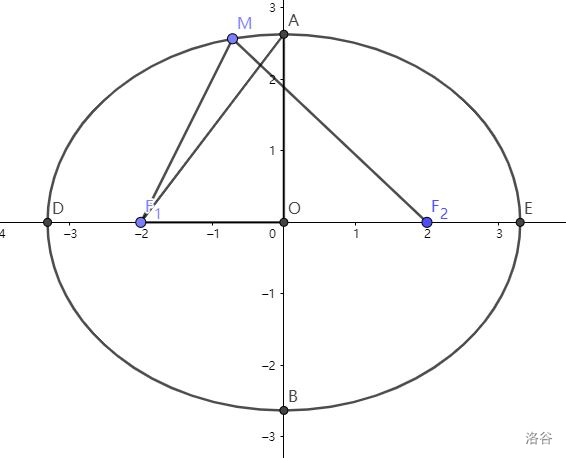
连接 \(AF_1\)，因为 \(F_1O=c,AO=b,b^2=a^2-c^2\)，根据勾股定理，\(AF_1=a\)。

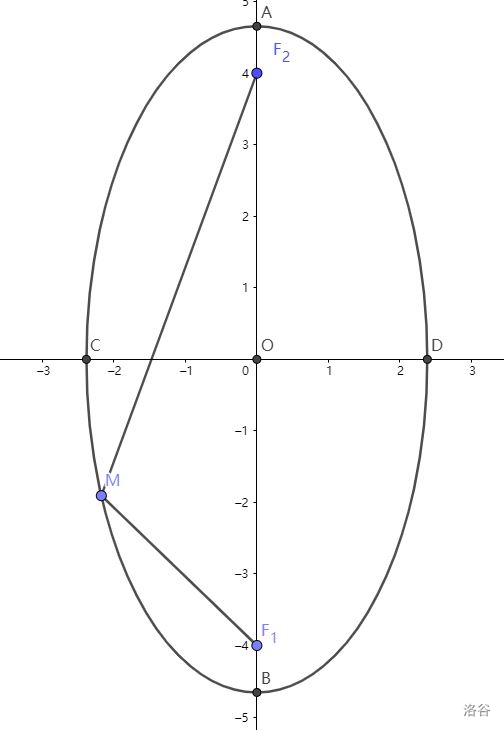
当椭圆是立起来的时候，\(\cfrac{x^2}{b^2}+\cfrac{y^2}{a^2}=1\)，推导就是照葫芦画瓢。

接下来定义椭圆的离心率 \(e=\cfrac{c}{a}\)。

\(F_1F_2\) 可以称为焦距，它的一半即 \(OF_1\) 可称为焦半距。

那么椭圆的离心率的定义就是椭圆上焦距与长轴的比值。其范围 \((0<e<1)\)

在几何意义上，椭圆的离心率越大，椭圆越扁；越小则越圆。

有点小想法：如果焦距等于零，也就是两焦点重合，此时就成了一个圆，它的 \(e=\cfrac{c}{a}=\cfrac{0}{r}=0\)，同时椭圆的方程 \(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\) 就变成了 \(\cfrac{x^2}{r^2}+\cfrac{y^2}{r^2}=1\) 而得到圆的方程 \(x^2+y^2=r^2\)。