DP

number triangles

感觉都与方格密切相关，比较好懂，重点在于对信息的分析（手玩）

1. AcWing 1018. 最低通行费

题意：一个\(n*n\)的方格，每个格子由一定的通行费，一个格子花费1个时间，要求在\(2*n-1\)的时间内从左上走到右下，求完成时的最低通行费。

分析：显然，必须走最短路，即\(→\)或\(↓\)，其它与模板无异。

\(code:\)

int main(){
    scanf("%d",&n);
    memset(f,0x3f,sizeof f);
    for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&f[i][j]);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(i==j and i==1) continue;
            f[i][j]=min(f[i-1][j],f[i][j-1])+f[i][j];
        }
    }
    printf("%d\n",f[n][n]);
    return 0;
}

注意边界，必须从\((1,1)\)点出发，所以有一点不同。

2.P1004 [NOIP2000 提高组] 方格取数

题意：设有 \(N \times N\) 的方格图 \((N \le 9)\)，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 \(0\)。如下图所示（见样例）:

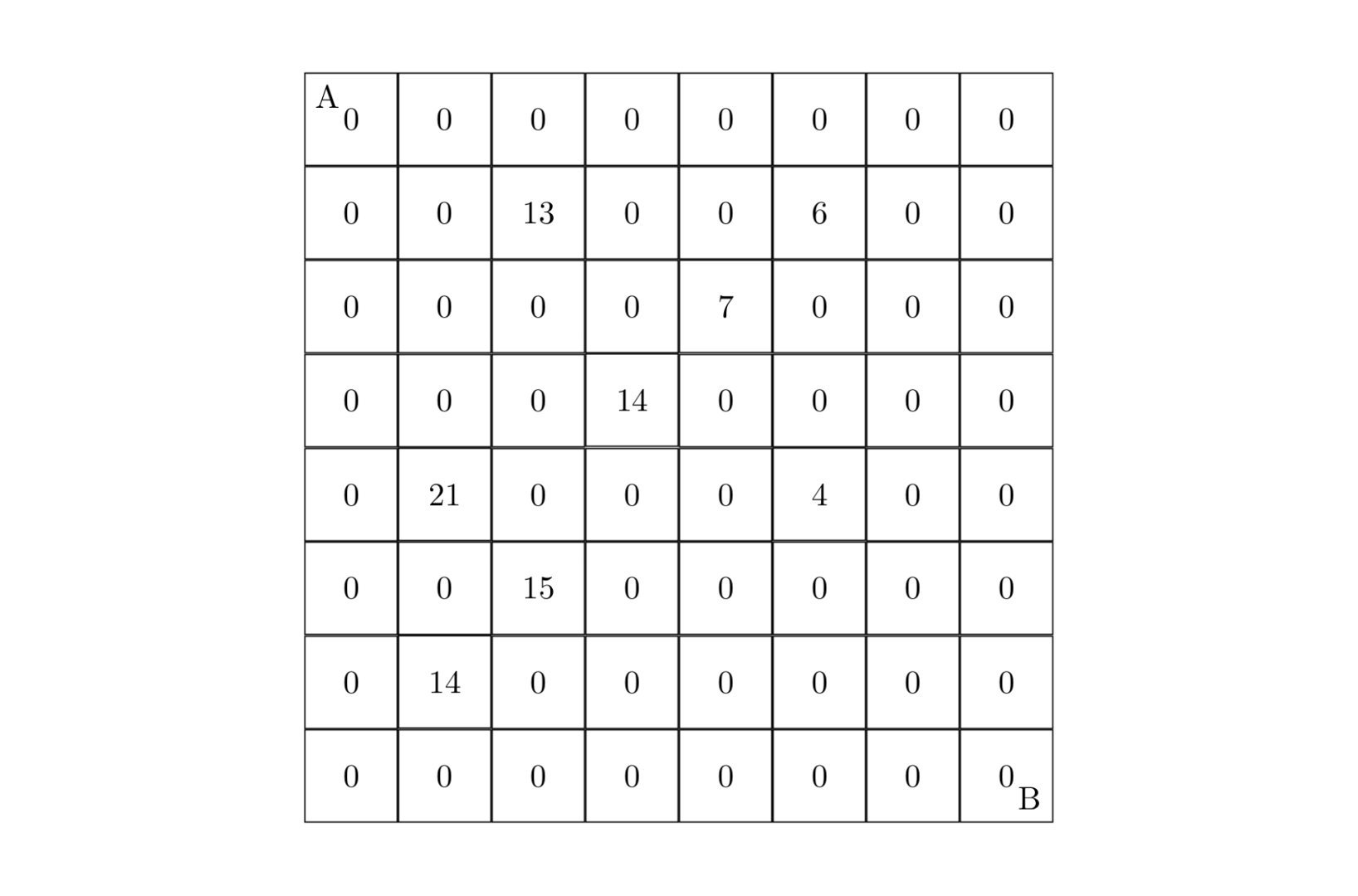
某人从图的左上角的 \(A\) 点出发，可以向下行走，也可以向右走，直到到达右下角的 \(B\) 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 \(0\)）。
此人从 \(A\) 点到 \(B\) 点共走两次，试找出 \(2\) 条这样的路径，使得取得的数之和为最大。

分析：状态新加2个维度，表示第二次所走的列和行，状态转移相同，但是如果第二次和第一次不同则再加一遍。

\(code:\)

rep(i,1,n){
    rep(j,1,n){
        rep(p,1,n){
            rep(q,1,n){
                int t1=max(f[i][j-1][p-1][q],f[i][j-1][p][q-1]);
                int t2=max(f[i-1][j][p-1][q],f[i-1][j][p][q-1]);
                f[i][j][p][q]=max(t1,t2)+g[i][j];
                if(i!=p and j!=q) f[i][j][p][q]+=g[p][q];
            }
        }
    }
}
printf("%d\n",f[n][n][n][n]);
return 0;